
Математика, теория+расчетные 1 семестр
.pdf
|
ОГЛАВЛЕНИЕ |
|
I. Матрицы, определители, системы линейных уравнений...................... |
7 |
|
Теория.............................................................................................................. |
7 |
|
1. |
Операции над матрицами, виды матриц и их свойства..................... |
7 |
2. |
Определители........................................................................................ |
11 |
3. |
Обратная матрица. ............................................................................... |
14 |
4. |
Матричная запись системы линейных уравнений. Решение |
|
матричных уравнений. Правило Крамера............................................ |
17 |
|
5. |
Ранг матрицы. Совместность системы линейных уравнений. ........ |
19 |
6. |
Метод Гаусса (метод последовательного исключения неизвестных) |
|
решения систем линейных уравнений................................................... |
21 |
|
Расчетные задания ...................................................................................... |
26 |
|
Методические указания.............................................................................. |
30 |
|
II. Векторы. ..................................................................................................... |
32 |
|
Теория............................................................................................................ |
32 |
|
1. |
Операции над векторами..................................................................... |
32 |
2. |
Скалярное произведение векторов. .................................................... |
35 |
3. |
Векторное произведение двух векторов............................................. |
35 |
4. |
Смешанное произведение векторов.................................................... |
36 |
Расчетные задания ...................................................................................... |
37 |
|
Методические указания. ............................................................................. |
38 |
|
III. Элементы аналитической геометрии..................................................... |
39 |
|
Теория............................................................................................................ |
39 |
|
1. |
Прямая на плоскости. Уравнения прямой. ....................................... |
39 |
2. |
Взаимное расположение прямых........................................................ |
41 |
4
3. |
Кривые второго порядка. Эллипс. Гипербола. Парабола. ............... |
42 |
4. |
Полярная система координат.............................................................. |
46 |
5. |
Плоскость в пространстве. Уравнения плоскости. ............................ |
49 |
6. |
Прямая в пространстве. ....................................................................... |
50 |
7. |
Взаимное расположение прямой и плоскости. .................................. |
51 |
8. |
Поверхности второго порядка.............................................................. |
51 |
9. |
Элементарная теория линейных операторов.................................... |
53 |
10. Собственные значения и собственные векторы линейного |
|
|
оператора. .................................................................................................. |
56 |
|
11. Квадратичные формы ........................................................................ |
58 |
|
Расчетные задания ...................................................................................... |
62 |
|
Методические указания.............................................................................. |
66 |
|
IV. Предел последовательности и функции одной переменной................ |
70 |
|
Теория............................................................................................................ |
70 |
|
1. |
Предел числовой последовательности ............................................... |
70 |
2. |
Бесконечно малые и бесконечно большие числовые |
|
последовательности. ................................................................................. |
71 |
|
3. |
Предел функции. .................................................................................. |
72 |
4. |
Непрерывность функции. .................................................................... |
76 |
Расчетные задания ...................................................................................... |
77 |
|
Методические указания.............................................................................. |
82 |
|
V. Дифференциальное исчисление функции одной переменной............ |
84 |
|
Теория............................................................................................................ |
84 |
|
1. |
Производная функции, основные правила дифференцирования. . |
84 |
5
2. |
Производная показательно- степенной и неявно заданной |
|
функции. .................................................................................................... |
86 |
|
3. |
Производные высших порядков. Производная параметрически |
|
заданной функции. ................................................................................... |
88 |
|
4. |
Дифференциал функции. .................................................................... |
90 |
5. |
Раскрытие неопределенностей. Правило Лопиталя. ....................... |
91 |
6. |
Исследование функций с помощью производной. Возрастание и |
|
убывание функций. .................................................................................. |
93 |
|
7. |
Выпуклость и вогнутость кривой. Точки перегиба. .......................... |
94 |
8. |
Асимптоты. Схема исследования функции. ...................................... |
95 |
9. |
Наибольшее и наименьшее значения функции на отрезке............ |
98 |
Расчетные задания ...................................................................................... |
99 |
|
Методические указания. ........................................................................... |
104 |
|
Библиографический список...................................................................... |
108 |
|
6

I. Матрицы, определители, системы линейных уравнений
Теория
1. Операции над матрицами, виды матриц и их свойства
Определение. Прямоугольная таблица m·n чисел, расположенных в m строках и n столбцах называется прямоугольной (m х n) матрицей.
Числа m и n называются порядками или размерностями матрицы. Если m=n, то матрица называется квадратной матрицей порядка m. Некоторые часто встречающиеся виды матриц имеют собственные
названия: |
|
|
|
матрица-строка, A ={a1 j } |
|
|
=(a11 ... a1n ), m =1; |
|
|
||
|
j=1, n |
||
a11
матрица-столбец, A ={ai1}i=1, m = ... , n =1;
am1
|
|
|
|
|
a |
|
0 |
... |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
11 |
|
a22 |
|
|
|
|
|
|
aii , i = j, |
диагональная матрица, A ={a |
} |
|
|
= 0 |
|
... |
0 |
, a |
= |
||||||
|
|
|
|
|
|
|
|||||||||
|
ii |
i=1, n |
... |
|
... |
... |
... |
ij |
|
||||||
|
|
|
|
|
|
0, i ≠ j, |
|||||||||
|
|
|
|
|
|
0 |
|
0 |
... |
|
|
|
|
|
|
|
|
|
|
|
|
|
ann |
|
|
|
|
||||
1 |
0 ... |
0 |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
i = j, |
|
|
||
единичная матрица, E = 0 |
1 ... |
0 |
, |
a |
= |
δij = |
1, |
диагональная |
|||||||
... ... ... |
... |
ij |
|
|
|
i ≠ j, |
|
|
|||||||
|
|
|
0, |
|
|
||||||||||
|
0 ... |
1 |
|
|
|
|
|
|
|
|
|
|
|||
0 |
|
|
|
|
|
|
|
|
|
|
|||||
матрица, у которой все диагональные элементы – единицы, а осталь-
1, |
i = j, |
– так называемый символ Кронекера; |
ные – нули; δij = |
i ≠ j, |
|
0, |
|
7

верхняя треугольная матрица,
|
|
|
a |
a ... |
a |
|
|
|
|
|
|
|
|
|
11 |
12 |
|
1n |
|
|
|
|
|
A ={aij } |
= |
0 |
a22 ... |
a2n |
, m = n,aij |
= 0 приi > j , |
|||||
|
|
m,n |
|
|
|
... |
|
|
|
|
|
|
|
|
... ... ... |
|
|
|
|
|
|||
|
|
|
0 |
0 ... |
ann |
|
|
|
|
||
нижняя треугольная матрица, |
|
|
|
||||||||
|
|
|
a |
0 ... |
0 |
|
|
|
|
|
|
|
|
|
11 |
|
|
|
|
|
|
|
|
A ={aij } |
= |
a21 |
a22 ... |
0 |
|
, m = n,aij |
= 0 приi < j , |
||||
|
|
m,n |
|
|
|
... |
|
|
|
|
|
|
|
|
... ... ... |
|
|
|
|
|
|||
|
|
|
an1 |
an2 ... |
ann |
|
|
|
|
||
ступенчатая матрица, |
|
|
|
|
|
|
|||||
a11 |
a12 |
a13 |
... |
a1r |
... |
|
a1n |
|
|
||
|
0 |
a |
a |
... |
a |
... |
|
a |
|
|
|
|
|
22 |
23 |
|
2r |
|
|
2n |
|
|
|
|
0 |
0 |
a33 |
... |
a3r |
... |
|
|
|
|
|
|
|
a3n |
|
|
|||||||
A = ... ... ... ... ... |
... |
|
... |
, r ≤ min(m, n), a ≠ 0 только если i < j ≤ r и |
|||||||
|
0 |
0 |
0 |
... |
a |
... |
|
a |
|
|
ij |
|
0 |
0 |
0 |
... |
rr |
... |
|
rn |
|
|
|
|
0 |
|
0 |
|
|
|
|||||
|
|
|
|
|
|
... |
|
... |
|
|
|
... ... ... ... ... |
|
|
|
|
|||||||
|
0 |
0 |
0 |
... |
0 |
... |
0 |
|
|
|
|
|
|
|
|
||||||||
др.
Определение. Две матрицы называются равными, если они имеют одинаковую размерность и равные соответственные элементы:
A ={aij }m,n , B ={bij }k ,l , A = B m = k,n = l,aij = bij , i =1, m, j =1,n.
Определение. Суммой двух матриц одинаковой размерности на- зывается матрица той же размерности, каждый элемент которой равен
сумме |
|
соответствующих |
элементов |
слагаемых: |
|
A ={aij } |
m,n |
, B ={bij } |
, C = A + B ={aij +bij } |
. |
|
|
|
m,n |
m,n |
|
|
8

Определение. Произведением матрицы на число называется мат-
рица той же размерности, каждый элемент которой равен произведению соответствующего элемента на число: A ={aij }m,n , B = α A ={ε aij}m,n
Для операций сложения и умножения матрицы на число справед- ливо:
1.1·A=A,
2.0·A= Θ,
3.a (βA) = (ab)A,
4.A+(B+C) = (A+B)+C,
5.A+B = B+A,
6.(a+b)A=aA+bA,
7.a(A+B) = aA+aB,
где A, B, C – произвольные матрицы одинаковой размерности, Θ – нуле- вая матрица той же размерности (читается «тэта»), a и b – произвольные числа.
Определение. Пусть заданы две матрицы A и B, причем число столбцов первой из них равно числу строк второй. Если
a11 |
a12 |
... |
a1n |
|
b11 |
b12 |
... |
b1k |
|
|
|
a |
a |
... |
a |
|
, |
b |
b |
... |
b |
|
, |
A = 21 |
22 |
|
2n |
B = 21 |
22 |
|
2k |
||||
|
|
... |
... |
|
|
|
|
... |
... |
|
|
... ... |
|
|
... ... |
|
|
||||||
am1 |
am2 |
... |
amn |
|
bn1 |
bn2 |
... |
bnk |
|
||
то произведением матриц A и B называется матрица
c11 |
... |
c1k |
|
|
c |
... |
c |
|
, |
C = 21 |
... |
2k |
||
... |
... |
|
||
cm1 |
... |
cmk |
|
|
элемент cij которой есть сумма произведений элементов i-й строки мат- рицы А на соответствующие элементы j-го столбца матрицы В:
cij = ai1 b1 j + ai2 b2 j +... + ain bnj , i =1,m j =1,k ;
9
произведение матриц A и B обозначается AB: C = AB. |
|
|
|
|
|
||||||||||||||
1 2 |
Пример. |
|
1 |
1 |
+ 2 |
0 1 (−1) |
+ 2 3 1 2 + 2 (−4) |
1 5 |
−6) |
||||||||||
|
1 |
−1 2 |
|
||||||||||||||||
|
3 |
4 |
|
|
3 |
1 |
+ 4 |
0 |
3 (−1) |
+ 4 3 |
3 2 + 4 (−4) |
|
3 |
9 |
−10 |
|
|||
|
|
|
3 −4 |
|
= |
= |
. |
||||||||||||
|
5 |
6 |
|
0 |
|
|
5 |
1 |
+ 6 |
0 |
5 (−1) |
+ 6 3 |
5 2 + 6 (−4) |
|
5 |
13 |
−14 |
|
|
|
|
|
|
|
|
|
|
||||||||||||
Для произведения матриц соответствующих порядков справедливо:
1.A·B ≠ B·A,
2.(A + B) · C = A·C + B·C,
3.C·(A + B) = C·A + C·B,
4.a(A·B) = (aA) B,
5.(A·B) C = A·(B·C).
Если AB = BA, то матрицы A и B называются перестановочными. Единичная матрица обозначается буквой E или En, где n – поря-
док матрицы. Основное свойство единичной матрицы AE=EA=A. Определение. Матрица, получающаяся из матрицы A заменой
строк соответствующими столбцами, называется транспонированной по отношению к матрице A и обозначается AT:
a11 |
a12 |
... |
a1n |
|
a11 |
a21 |
... |
am1 |
|
|
a |
a |
... |
a |
|
, |
a |
a |
... |
a |
|
A = 21 |
22 |
|
2n |
AT = 12 |
22 |
|
m2 |
. |
||
|
|
... |
... |
|
|
|
|
... ... |
|
|
... ... |
|
|
... ... |
|
||||||
am1 |
am2 |
... |
amn |
|
a1n |
a2n |
... |
amn |
|
|
Для операции транспонирования справедливо:
1.(aA + bB)T = a A T + bB T,
2.(AB)T = B TA T .
Квадратная матрица A, для которой AT = A, называется симметрич-
ной.
Определение. Элементарными называются следующие преобра- зования матриц:
-умножение строки или столбца на число, отличное от нуля;
-прибавление к строке или столбцу линейной комбинации других строк или столбцов (соответственно);
-перестановка двух любых строк или столбцов.
10
2. Определители
Для каждой квадратной матрицы определено число, называемое
определителем или детерминантом матрицы.
Определение. Определителем квадратной матрицы первого по- рядка называется число, равное единственному элементу этой матрицы:
A={a}, detA=|A|=a.
Пусть A – произвольная квадратная матрица порядка n, n>1:
a11 |
a12 |
... |
a1n |
|
a |
a |
... |
a |
|
A = 21 |
22 |
|
2n . |
|
|
|
... |
... |
|
... ... |
|
|||
an1 |
an2 |
... |
ann |
|
Определение. Минором элемента матрицы называется определи- тель матрицы, полученной вычеркиванием строки и столбца, в которых расположен элемент. Обозначают минор элемента aij – M ij .
Определение. Алгебраическим дополнением элемента матрицы называется его минор, умноженный на (–1) в степени, равной сумме но- меров строки и столбца, в которых расположен элемент. Обозначают ал-
гебраическое дополнение элемента aij – |
Ai j . |
|
|
|||||||||||||||
|
Пример. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
1 |
2 |
3 |
|
|
|
|
|
|
|
|
1 2 |
|
|
|
|
|
|
A = |
4 |
5 |
6 |
, a |
23 |
= 6, M |
23 |
= |
=1 |
8 − 2 7 |
= −6, A = (−1)2+3 M |
23 |
= −(−6) = 6 . |
|||||
|
|
|
|
|
|
|
|
|
|
|
7 8 |
|
|
23 |
|
|||
|
7 |
8 |
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Определение. Определителем n-го порядка (определителем квад- |
|||||||||||||||||
ратной матрицы n-го порядка n), n>1, называется число, равное |
||||||||||||||||||
det A = |
|
a11 |
a12 |
... |
a1n |
|
|
=∑(−1)1+ j a1, j |
M1 j , |
|
|
|
||||||
|
|
|
|
|
||||||||||||||
|
a21 |
a22 |
... |
a2n |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
||
|
|
|
... |
... |
... |
... |
|
|
|
j=1 |
|
|
|
|
||||
|
|
|
an1 |
an2 |
... |
ann |
|
|
|
|
|
|
|
|
|
|
||
где M1 j – определитель квадратной матрицы полученной из матрицы A
вычеркиванием первой строки и j-го столбца.
Для определителей 2-го и 3-го порядка легко получить простые вы- ражения через элементы матрицы.
11
Определитель 2-го порядка:
a11 |
a12 |
=(−1)1+1 a |
M |
11 |
+(−1)1+2 a |
|
M |
12 |
= a |
a |
− a |
a . |
|
|
|||||||||||||||||||||
a21 |
a22 |
|
|
|
|
|
|
11 |
|
|
|
|
|
|
|
|
12 |
|
|
11 |
22 |
|
12 |
21 |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
Определитель 3-го порядка: |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
a11 |
a12 |
|
a13 |
|
=(−1)1+1 a M |
|
|
+(−1)1+2 a M |
|
++(−1)1+3 a M |
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
a |
21 |
|
a |
22 |
|
a |
23 |
|
11 |
|
12 |
13 |
= |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11 |
|
|
|
|
|
|
12 |
|
|
13 |
|
|||||||||
|
a31 |
a32 |
|
a33 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
= a |
|
a22 |
a23 |
|
− a |
|
a21 |
a23 |
|
|
+ a |
|
a21 |
a22 |
|
= |
|
|
|
|
|
. |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
11 |
|
|
a |
a |
|
|
12 |
|
|
a |
|
a |
|
|
|
13 |
|
a |
|
a |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
32 |
|
33 |
|
|
|
|
|
|
|
31 |
33 |
|
|
|
|
|
|
31 |
32 |
|
|
|
|
|
|
|
|
||||
=a11 (a22a33 − a23a32 )− a12 (a21a33 − a23a31 )+ a13 (a21a32 − a22a32 )=
=a11a22a33 + a21a32a13 + a12a23a31 − a13a22a31 − a11a32a23 − a33a21a12 .
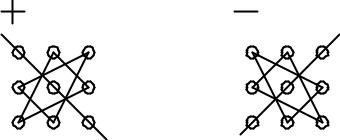
Последнюю формулу нетрудно запомнить. Если соединить линией каждые три множителя со знаком « +» в слагаемых определителя, то по- лучим схему 1. Аналогично для произведений, входящих со знаком «–», получаем схему 2.
Схема 1 |
Схема 2 |
Это правило вычисления определителей 3-го порядка называется правилом треугольников.
Теорема. Определитель n-го порядка, n>1, равен сумме произве- дений элементов любой строки (столбца) на их алгебраические дополне- ния.
|
|
1 |
2 |
3 |
|
|
Пример. 1. Вычислим определитель матрицы |
|
4 |
5 |
6 |
|
раз- |
A = |
|
|||||
|
|
7 |
8 |
9 |
|
|
|
|
|
|
ложением по элементам первой строки;
12
det A = (−1)1+1 1 M11 + (−1)1+2 2 M12 + (−1)1+3 3 M13 |
=1 |
5 |
6 |
− 2 |
4 |
6 |
+3 |
4 |
5 |
= |
|
|
8 |
9 |
|
7 |
9 |
|
7 |
8 |
|
=(−3) − 2 (−6) +3 (−3) = −3 +12 −9 = 0.
2.Получим тот же результат разложением определителя по элементам второй строки:
1 |
2 |
3 |
=(−1)2+1 4 M21 +(−1)2+2 5 M22 +(−1)2+3 6 M23 =−4 |
|
2 |
3 |
|
+5 |
|
1 |
3 |
|
−6 |
|
1 |
2 |
|
= |
|
|
|
|
|
|
|||||||||||||
4 |
5 |
6 |
|
|
|
|
|
|
||||||||||
7 |
8 |
9 |
|
|
8 |
9 |
|
|
|
7 |
9 |
|
|
|
7 |
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
=(−4) (−6) +5 (−12) −6 (−6) =24 −60 +36 =0.
Для определителей справедливы следующие свойства.
1.Определитель не изменяется при транспонировании: detAT=detA.
2.Если строка (столбец) матрицы A равна линейной комбинации соответственных строк (столбцов) матриц A и B, а остальные строки (столбцы) этих матриц совпадают, то ее определитель равен линейной комбинации определителей матриц A и B:
Ai = a·Bi + b·Ci, detA = a·detB + b·detC, A(j) = a·B(j) + b·C(j), detA = a·detB + b·detC .
3.При перестановке любых двух строк (столбцов), определитель ме- няет знак.
4.Если в определителе есть две одинаковые строки (два одинако- вых столбца), то он равен нулю.
5.Если в определителе есть две пропорциональные строки (два пропорциональных столбца), то он равен нулю.
6.Определитель не изменится, если к элементам любой его строки (столбца) прибавить элементы любой другой строки (столбца), умножен- ные на одно и то же число.
7.Определитель, содержащий нулевую строку (нулевой столбец), равен нулю.
8.Сумма произведений элементов любой строки (столбца) на алгеб- раические дополнения другой строки (другого столбца) равна нулю.
9.Определитель произведения матриц равен произведению опре- делителей сомножителей.
Теорема. Определитель треугольной матрицы равен произведе- нию диагональных элементов.
13
