
Математика, теория+расчетные 1 семестр
.pdf
4)вектор −a называется противоположным вектору a ; вектор −a
имеет длину равную длине вектора a , но противоположное на- правление, т.е.
5)a + (−a) = 0 .
Определение. Разностью двух векторов a и b будем называть
а
|
|
|
|
|
c |
|
c |
= |
a |
− |
b |
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
b |
b |
|
|
|
|
|
|
|
|
|
||
|
|
Рис. 3 |
|
|
|
|
|
|
|
|||
сумму векторов a и −b , т.е. a + (−b) .
Определение. Произведением вектора a на число λ называется вектор c длины |c | = |λ| a , направление которого совпадает с направле-
нием a , если λ > 0, противоположно a , если λ < 0. При λ=0 c =0. Операция умножения вектора на число обладает свойствами:
1.( α+β ) а=αа+βа, где α,β R;
2.α(а+b )=αа+αb ;
3.α(βа)=(αβ)а;
4.1×а=а, (-1)× а=-а, 0×а=0.
Определение. Два вектора а и b называются коллинеарными, ес- ли они расположены на одной прямой или на параллельных прямых.
Теорема. Для того чтобы два вектора а и b были коллинеарны, необходимо и достаточно, чтобы они были пропорциональны, т.е. имело место равенство b =λа, λ R.
Определение. Три или более векторов называются компланарны- ми, если они лежат в одной плоскости или в параллельных плоскостях.
Теорема. Для того чтобы три вектора а, b , с были компланарны- ми необходимо и достаточно, чтобы один из них был линейной комбина-
цией двух других, т.е. с=αа +βb , α,β R.
34

Определение. Проекцией вектора а на ось Z называется число аZ =аcosϕ, где ϕ − угол между вектором а и направлением оси Z. Проек- ция вектора a на ось Z обозначается символом аZ = прZ а
2. Скалярное произведение векторов
Определение. Скалярным произведением двух векторов а и b на- зывается число, равное произведению модулей этих векторов и косинуса
угла между ними. Скалярное произведение векторов а и b обозначается
символом а b или (а,b ) , т.е. (а,b )=ab cosϕ .
Из определения следует, что косинус угла ϕ между не нулевыми
векторами а и b находится по формуле cos ϕ= (a,b) . a b
Свойства скалярного произведения векторов:
1)(а,b )=(b , а);
2)(a +b,c) = (a,c) + (b,c) ;
3)a2 = (a,a) = a2 ;
4)(λa,b) = λ(a,b) ;
5)(λa + μb,c) = λ(a,c) + μ(b,c) .
Теорема. Ненулевые векторы а и b перпендикулярны лишь в том
случае, если их скалярное произведение равно |
нулю, т.е. ( |
а |
, |
b |
)=0; |
||||
cos ϕ=0; ϕ=π/2. |
|
|
|
|
|
||||
Теорема. Если векторы |
|
и |
|
заданы в |
координатной форме |
||||
а |
b |
||||||||
a = axi + ay j + az k, b = bx i + by j + bz k , то (a,b) = axbx + a yby + azbz .
Следствие. Косинус угла ϕ между двумя векторами а и b , задан- ными координатами, определяется по формуле
cosϕ = |
|
axbx |
+ ayby + azbz |
|
. |
||
a2 |
+ a2 |
+ a2 |
b2 |
+b2 |
+b2 |
||
|
x2 |
y |
z |
x |
y |
z |
|
3. Векторное произведение двух векторов
Определение. Три вектора а, b , с образуют правую тройку, если движение вектора а к вектору b по меньшему углу совершается против часовой стрелки, при наблюдении с конца вектора с.
35

Например, орты i , j , k правой системы координат образуют правую тройку векторов.
Определение. Векторным произведением двух векторов а и b на-
зывается третий вектор с , обозначаемый символом а × b и удовлетво- ряющий условиям:
1. Модуль вектора с равен площади параллелограмма, построенного на векторах а и b т.е., c = ab sin ϕ , где ϕ − угол между этими векторами.
2.Вектор с ортогонален векторам а и b .
3.Тройка векторов а, b , с − правая.
Свойства векторного произведения.
1)а × b =- b × а;
2)а × а= 0;
3)(λa ×b) = (a × λb) = λ(a ×b) ;
4)( а+b )×с=a × c +b × c .
Теорема. Если векторы а и b заданы в координатах, т.е.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
j |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a = axi + ay j + az k , |
b = bxi +by j +bz k , то |
а×b =det ax |
ay |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
a |
y |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|||
k az . bz
Теорема. Площадь S треугольника, построенного на векторах а и b , можно вычислить по формуле S = ½ |а×b |
Теорема. Для того чтобы векторы были коллинеарны, необходимо и достаточно, чтобы их векторное произведение было равно нуль вектору,
т.е. а×b = 0.
4. Смешанное произведение векторов
Определение. Смешанным произведением трех векторов а, b , с называется число, равное скалярному произведению векторного произ-
ведения векторов а и b на вектор с , обозначаемое символом ( а,b ,с), т.е. ( а,b ,с)=( а×b )с.
Теорема. Смешанное произведение трех векторов а,b , с численно
равно объему параллелепипеда, построенного на векторах а,b , с и взя-
36
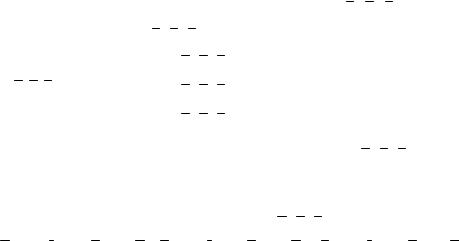
тому со знаком «плюс», если тройка а, b , с - правая и со знаком «ми-
нус»,если тройка а,b ,с - левая, т.е.
V
(a,b,c) = −V
O
,если а,b ,с правая тройка,
,если а,b ,с левая тройка,
,если а,b ,с компланарны.
Теорема. Для того чтобы векторы a ,b , с были компланарны, необ- ходимо и достаточно, чтобы их смешанное произведение было равно ну- лю.
Теорема. Пусть векторы a ,b ,с заданы в координатах a = axi + ay j + az k , b = bx i +by j +bx k , c = cxi + cy j + cz k .
|
|
|
|
|
|
ax |
ay |
az |
||
|
|
|
|
|
|
|
b |
|
b |
|
|
|
|
|
|
|
|||||
Тогда ( a ,b ,с)=det b |
|
. |
||||||||
|
|
|
|
|
|
x |
|
y |
z |
|
|
|
|
|
|
|
cx |
cy |
cz |
|
|
Расчетные задания
Задача 3. Найти скалярное и векторное произведения векторов
2ar +b и 3ar − 2b , площадь параллелограмма построенного на векторах |
|||||||||||
r |
r |
r |
|
|
|
|
|
|
|
|
|
a +b и 3a |
−b . |
|
|
|
3.2. аr = 5i + j + k , |
|
|
|
|||
3.1. аr = 5i − j +9k , |
|
b = 2i +3 j −6k . |
b = i + j + k |
||||||||
3.3. аr = −5i + j −9k , |
b = −2i − j + 6k . |
3.4. аr = −5i |
− 2 j − 2k ,b = −2i − 3 j + 4k . |
||||||||
3.5. аr = −i |
− j − k , |
b = i − 2 j − 7k . |
3.6. аr = i |
+ j + k , |
b = −4i |
−5 j . |
|||||
3.7. аr = i |
− 2 j − 2k , |
|
b = −3i − 2 j − 4k . |
3.8. аr = 5i |
+ 3 j + k , |
b = 3i |
+ 3 j − k . |
||||
3.9 . аr = 5i + 3 j + 4k , |
b = i + 2 j − 6k . |
3.10. аr = −2i − 2 j + k , |
b = −2i − 7k . |
||||||||
3.11. аr = −3ir − 2kr, |
b = −3ir −5 rj + 4k . |
3.12. аr = −i |
−3 j − k , |
br = 7ir − rj + 7k . |
|||||||
3.13. аr = 4i − j + k , |
|
b = −i |
− 2 j . |
3.14. аr = 3i |
−3 j − k , |
b = j . |
|||||
3.15. аr = i |
− 4 j − 2k ,b =13i |
+10 j +15k . |
3.16. аr = i + 2 j + k , b = 6i − 6 j +13k . |
||||||||
37
3.17. аr = i − j + 2k , b = i + 2 j −5k . |
3.18. аr = −i |
− j + 4k , |
b = 3i − j + 2k . |
||||
3.19. аr = −5i −k , |
b = 2i +3k . |
3.20. аr = 6i + k , |
b = 3i + 6 j − 4k . |
||||
3.21. аr = −4i + 4 j + k , |
b = 5i + j . |
3.22. аr = 5i −9 j −5k , |
b = 3i − 4 j − 7k . |
||||
3.23. аr = −2i + 3 j −8k , |
b = 3i − j + 4k . |
3.24. аr = 5i , |
b = i − 2 j − 7k . |
||||
3.25. аr = j + k , |
b = −i + 2k . |
|
3.26. аr = −i + j − k , |
b = −i + j + k . |
|||
3.27. аr = −4i + 2 j − k , |
b = i |
− j − k . |
3.28. аr = 6i − 4k , |
b = 5i + 7 j + 6k . |
|||
3.29. аr = 2i + 3 j − 6k , |
b = 5i |
− j + 9k . |
3.30. аr = 2i + 3 j + 6k , |
b = 5i − j + 9k . |
|||
Методические указания
Задача 3. Вычислить векторное и скалярное произведения векто-
ров ar − 2b и ar + b и площадь параллелограмма, построенного на этих век-
торах, если ar = (1, 2, 3), br = (1, −3, 2) .
r |
|
|
Решение. Воспользуемся свойством векторного произведения |
|
|||||||||||||||||||
= |
|
r |
r r |
|
|
r |
|
|
|
r r |
|
|
|
r |
r |
|
|
r r |
|
||||
c |
|
[ a |
− 2 b , a |
+ b ] |
= [ a , a ] |
− 2[b , a ] + |
[ a , b ] |
− 2[b , b ] = 3[ a , b ] = |
|
||||||||||||||
= 3 |
|
ir |
rj |
kr |
|
= ir |
|
2 |
3 |
|
− rj |
|
1 3 |
|
+ kr |
|
1 |
2 |
|
= 11 ir + 5 rj − |
7 kr. |
||
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||
|
1 |
2 |
3 |
|
|
|
|
|
|
3 |
|||||||||||||
|
|
|
2 |
− 3 |
1 |
|
|
|
|
− |
3 1 |
|
|
|
2 1 |
|
|
|
2 |
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
Площадь параллелограмма равна модулю векторного произведе- |
||||||||||||||||||||
ния: | cr |= 112 + 52 + 72 |
= |
195 . |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
Скалярное произведение вычисляем, раскрывая скобки, и, исполь- |
||||||||||||||||||||
зуя его свойства: (ar − 2b, ar + b) = ar2 |
− 2arb + arb + b 2 |
=14 −1 +14 = 27 . |
|
||||||||||||||||||||
Ответ: c = (11, 5, 7) , S =  195 , (ar − 2b, ar + b) = 27 .
195 , (ar − 2b, ar + b) = 27 .
38

III. Элементы аналитической геометрии
Теория
1. Прямая на плоскости. Уравнения прямой
Теорема. Если на плоскости задана прямоугольная система Oxy , то всякое уравнение первой степени Ax + By + C = 0 определяет относи-
тельно этой системы прямую линию. Верно и обратное утверждение.
Теорема. Всякая прямая линия на плоскости с заданной прямо- угольной системой координат Oxy определяется уравнением первой сте-
пени.
Определение. Уравнение вида Ax + By + C = 0 с произвольными ко-
эффициентами A, B и C такими, что A и B не равны нулю одновремен- но, называется общим уравнением прямой. Вектор n ={A, B} называют
нормальным вектором прямой.
Теорема. Прямая, определяемая общим уравнением, ортогональна к вектору n ={A, B}.
Теорема. Если все коэффициенты A, B и C отличны от нуля, то уравнение Ax + By + C = 0 можно представить в виде ax + by =1 , где
a = −C / A , b = −C / B .Этот вид уравнения называется уравнением пря-
мой «в отрезках».
Определение. Любой ненулевой вектор, параллельный данной прямой, называют направляющим вектором этой прямой.
Теорема. Уравнение прямой, проходящей через данную точку M1 (x1, y1 ) с направляющим вектором q = {l,m} , имеет вид:
x −l x1 = y −my1 .
Это уравнение называется каноническим уравнением прямой.
Теорема. Уравнение прямой, проходящей через две данные точки M1 (x1, y1 ) и M 2 (x2 , y2 ) имеет вид:
39
x − x1 |
= |
y − y1 |
|
x2 − x1 |
y2 − y1 . |
||
Используя понятие определителя, его можно записать так:
|
|
|
|
|
|
x − x1 |
y − y1 |
|
= 0 . |
|||||
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
x |
2 |
− x |
y |
2 |
− y |
|
|
|
|
|
|
|
|
|
|
1 |
|
1 |
|
|
|||
Теорема. Обозначим |
через t |
значение отношений в каноническом |
||||||||||||
|
|
|
x − x1 |
|
= t , |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
l |
|
t R . |
|
Тогда |
|
уравнение прямой примет вид |
|||||
уравнении y − y |
|
|
|
|||||||||||
|
|
|
1 |
= t , |
|
|
|
|
|
|
|
|||
|
|
|
m |
|
|
|
|
|
|
|
|
|||
x = x1 |
+ lt , |
|
|
|
|
|
|
|
|
|
|
|
||
t R |
. Данные уравнения называются параметрическими |
|||||||||||||
|
+ mt , |
|||||||||||||
y = y1 |
|
|
|
|
|
|
|
|
|
|
|
|
||
уравнениями прямой.
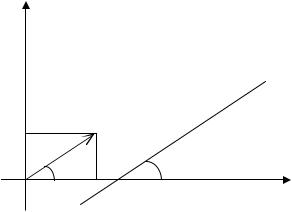
Определение. Тангенс угла наклона прямой к оси Ox называют
угловым коэффициентом прямой. Обозначим: k = tg α.
Если прямая не перпендикулярна оси Ox (рис. 4) и имеет направ-
Y
|
|
|
l |
|||
|
q |
|
|
|
|
|
α |
α |
|||||
0 |
|
|
X |
|||
|
|
|
Рис. 4 |
|||
ляющий вектор q ={l, m}, то угловой коэффициент k = |
m |
|
||||
l |
||||||
|
|
|
|
|||
Теорема. Уравнение прямой, проходящей через заданную точку |
||||||
M1 (x1, y1 ) и имеющей |
заданный угловой коэффициент k имеет вид |
|||||
y − y1 = k(x − x1 ) . Если |
обозначить b = y1 − kx1 , то это уравнение примет |
|||||
вид
y = kx + b .
40

Оно называется уравнением прямой с угловым коэффициентом.
Положение прямой l на плоскости однозначно определяется указа- нием расстояния p от начала координат до прямой ( p ≥ 0 ) и угла ϕ, кото-
Y
B
p
ϕ
0 |
A |
X |
|
|
Рис. 5 |
рый образует вектор, перпендикулярный к прямой, с положительным направлением оси Ox .
Ясно, что точки A и B , отмеченные на чертеже (рис. 5), имеют соот-
|
p |
|
|
|
|
p |
|
|
ветственно координаты |
;0 |
|
и |
0; |
. |
|||
|
|
|||||||
|
|
|
|
|
|
|
|
|
cosϕ |
|
|
|
|
sinϕ |
|||
Составим уравнение заданной прямой l в отрезках на осях:
|
x |
+ |
y |
=1 |
или |
|
p cosϕ |
p sinϕ |
|||
|
|
|
|
||
xcosϕ + ysinϕ − p = 0 , |
p ≥ 0 . |
||||
Это уравнение называется нормальным уравнением прямой. Век-
тор n0 ={cosϕ , sinϕ} является (единичным) вектором нормали прямой l .
2. Взаимное расположение прямых
Теорема. Пусть заданы две прямые, непараллельные оси Оу, уравнения которых имеют вид y = k1 x + b1, y = k2 x + b2 . Тогда
1)угол θ между этими прямыми определяется с помощью формулы
tg θ = |
k1 − k2 |
, 0 ≤ θ ≤ π. |
|
|
|||
|
1+ k k |
2 |
|
|
1 |
|
|
2)условие параллельности k1 = k2
41

3)условие перпендикулярности k1 k2 = -1
Теорема. Пусть прямые l1 и l2 заданы общими уравнениями
А х +В у +С =0, А1 х +В1 у +С1 =0. Тогда
1) при условии |
А |
≠ |
В |
прямые пересекаются, причем, если |
А |
|
А1 |
= −1 , |
|
А |
В |
В |
В |
||||||
|
|
|
|
|
|||||
|
1 |
|
1 |
|
|
|
1 |
|
то прямые перпендикулярны.
2)при условии
3)при условии
А
А1
А
А1
= В
В1
= В
В1
≠ С , прямые параллельны.
С1
= С , прямые совпадают.
С1
3. Кривые второго порядка. Эллипс. Гипербола. Парабола
Эллипс Определение. Эллипсом (рис. 6) называется геометрическое место
точек на плоскости, сумма расстояний от каждой из которых до двух данных точек F1 и F2 , называемых фокусами, есть величина постоянная 2а, большая чем расстояние между фокусами 2с.
|
Y |
|
|
|
|
|
b |
A3 |
|
|
|
|
|
|
|
M(x,y) |
|
|
γ2 |
|
γ1 |
|
|
A1 |
|
|
A2 |
||
|
0 |
|
|
||
-a |
F1(-c,0) |
F2(c,0) |
|
a X |
|
-b A4
Рис. 6
42
Каноническое уравнение эллипса имеет вид |
x2 |
+ |
y 2 |
=1 , где a2 – |
|
a 2 |
b2 |
||||
|
|
|
c2=b2.
Свойства эллипса
1.Эллипс является симметричной кривой относительно осей координат.
2.Ось симметрии, содержащая фокусы, называется фокальной осью. Точка пересечения осей симметрии называется центром эллипса.
3.Из уравнения эллипса следует, что кривая имеет точки пересечения
сосями координат: (-а,0); (а,0); (0,b),(0,-b).
4.Отрезки А2А1 и А3А4 называются соответственно большой и малой осями эллипса.
5.Фокусы эллипса лежат всегда на большей оси.
6.Величина ε = с/а называется эксцентриситетом эллипса. Так как
0≤с<a, то 0 ≤ ε < 1.
Геометрический смысл эксцентриситета.
1.Если ε = 0 , то эллипс является окружностью.
2.Если ε близко к 1, то овал эллипса «сильно» вытянут вдоль фо- кальной оси.
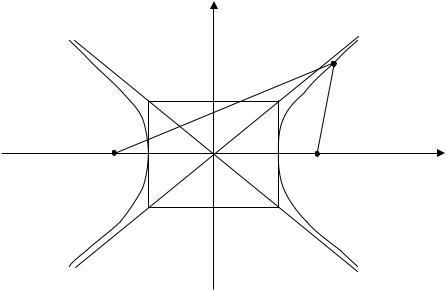
Гипербола Определение. Гиперболой (рис. 7) называется геометрическое ме-
сто точек плоскости, разность расстояний от каждой из которых до двух данных точек F1 и F2, называемых фокусами, есть величина постоянная 2а, меньшая чем расстояние между фокусами 2с.
|
Y |
|
|
|
b |
|
M(x,y) |
γ |
γ1 |
|
|
2 |
|
||
|
0 |
|
|
|
|
|
|
F1(-c,0) -a |
|
a F2(c,0) |
X |
-b
Рис. 7
43
