Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Нижегородский Государственный Технический Университет им. Р.Е. Алексеева

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Математика, теория+расчетные 1 семестр

.pdf

Скачиваний:

Добавлен:

28.03.2015

Размер:

767.71 Кб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 910 / 1110 11 > Следующая >>>

наименьшим значением на отрезке – это понятия принципиально раз- личные.

Определение. Точки максимума и минимума функции называют-

ся точками экстремума.

Теорема. (необходимое условие существования экстремума) Если функция f(x) дифференцируема в точке х = х1 и точка х1 является точкой экстремума, то производная функции обращается в нуль в этой точке.

Следствие. Обратное утверждение неверно. Если производная функции в некоторой точке равна нулю, то это еще не значит, что в этой точке функция имеет экстремум. Красноречивый пример этого – функ- ция у = х3, производная которой в точке х = 0 равна нулю, однако в этой точке функция имеет только перегиб, а не максимум или минимум.

Определение. Критическими точками функции называются точ- ки, в которых производная функции не существует или равна нулю.

Рассмотренная выше теорема дает нам необходимые условия суще- ствования экстремума, но этого недостаточно.

Теорема. (Достаточные условия существования экстремума) Пусть функция f(x) непрерывна в интервале (a, b), который содер-

жит критическую точку х1, и дифференцируема во всех точках этого ин- тервала (кроме, может быть, самой точки х1).

Если при переходе через точку х1 слева направо производная функ- ции f′(x) меняет знак с “+” на “−“, то в точке х = х1 функция f(x) имеет максимум, а если производная меняет знак с “−“ на “+”, то функция име- ет минимум.

7. Выпуклость и вогнутость кривой. Точки перегиба

Определение. Кривая обращена выпуклостью вверх на интервале (а, b), если все ее точки лежат ниже любой ее касательной на этом интер- вале. Кривая, обращенная выпуклостью вверх, называется выпуклой, а кривая, обращенная выпуклостью вниз – называется вогнутой.

Теорема 1. Если во всех точках интервала (a, b) вторая производ- ная функции f(x) отрицательна, то кривая y = f(x) обращена выпуклостью вверх (выпукла).

Определение. Точка, отделяющая выпуклую часть кривой от во- гнутой, называется точкой перегиба.

Очевидно, что в точке перегиба касательная пересекает кривую.

Теорема 2. Пусть кривая определяется уравнением y = f(x). Если вторая производная f′′(a) = 0 или f′′(a) не существует и при переходе че- рез точку х = а f′′(x) меняет знак, то точка кривой с абсциссой х = а явля- ется точкой перегиба.

8. Асимптоты. Схема исследования функции

Определение. Прямая называется асимптотой кривой, если рас- стояние от переменной точки кривой до этой прямой при удалении точки в бесконечность стремится к нулю.

Вертикальные асимптоты.

Из определения асимптоты следует, что если lim f (x ) = ∞ или

x →a +0

lim	f (x ) = ∞ или lim f (x ) = ∞, то прямая х = а – асимптота кривой y =
x →a −0	x →a
f(x).		2
	Например, для функции f (x ) =	2	прямая х = 5 является верти-
	Например, для функции f (x ) =	x − 5	прямая х = 5 является верти-
кальной асимптотой.		x − 5
кальной асимптотой.
	Наклонные асимптоты.
	Кривая y = f(x) имеет наклонную асимптоту y = kx + b, если
	k = lim f (x ) ,		b = lim[f (x ) − kx ].
	x →∞ x		x →∞

Горизонтальные асимптоты являются частным случаем наклонных асимптот при k =0.

Схема исследования функций.

1.Область существования функции. Это понятие включает в себя и область значений, и область определения функции.

2.Интервалы знакопостоянства. Точки пересечения с осями коор- динат.

3.Точки разрыва (если имеются).

4.Интервалы возрастания и убывания.

5.Точки максимума и минимума.

6.Максимальное и минимальное значение функции на ее области определения.

7.Области выпуклости и вогнутости.

8.Точки перегиба (если имеются).

9.Асимптоты (если имеются).

10.Построение графика.

Применение этой схемы рассмотрим на примере.

Пример. Исследовать функцию y =	x 3	и построить ее график.
	x 2 −1

1.Находим область существования функции. Очевидно, что обла- стью определения функции является область (-∞; -1) (-1; 1) (1; ∞).

2.В свою очередь, видно, что прямые х = 1, х = -1 являются верти-

кальными асимптотами кривой.

Областью значений данной функции является интервал (-∞; ∞). Точками разрыва функции являются точки х = 1, х = -1.

3. Интервалы знакопостоянства:

При x (−∞;−1) (0;1) график расположен ниже оси ОХ, при

x(1,+∞) (−1;0) выше оси ОХ.

4.Функция нечетная, так как y(−x) = −y(x) , график симметричен

относительно начала координат.

5. Находим критические точки.

Найдем производную функции

	′		3x 2	(x 2 −1) − 2x x 3		3x 4 − 3x 2 − 2x 4	x 4 − 3x 2
y		=		(x 2 −1)2	=	(x 2 −1)2	= (x 2 −1)2 .

Критические точки: x = 0; x = -						3 ; x = 3 ; x = -1; x = 1.

Находим промежутки возрастания и убывания функции. Для этого определяем знаки производной функции на промежутках.

-∞ < x < -		3 ,	y′ > 0, функция возрастает;
-	3 < x < -1,		y′ < 0, функция убывает;
-1 < x < 0,			y′ < 0, функция убывает;
0	< x < 1,		y′ < 0, функция убывает;
1	< x <	3 ,	y′ < 0, функция убывает;
	3 < x < ∞,		y′′ > 0, функция возрастает.

Видно, что точка х = - 3 является точкой максимума, а точка х = 3 является точкой минимума. Значения функции в этих точках равны

соответственно -3 3 /2 и 3 3 /2.

6. Найдем вторую производную функции

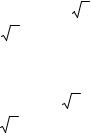
y ′′ = (4x 3 −6x )(x 2 −1)2 −(x 4 − 3x 2 )4x (x 2 −1)

(x 2 −1)4

(4x 3 −6x )(x 4

− 2x

2 +1) −(x 4 − 3x 2 )(4x 3 − 4x )

(x 2 −1)4

4x 7 − 8x 5 + 4x 3 −6x 5 + 12x 3 −6x − 4x 7 + 4x

5 + 12x 5 −12x 3

(x 2 −1)4

2x 5 + 4x 3 −6x

2x (x 4 + 2x 2 − 3)

2x (x 2 + 3)(x 2 −1)

2x (x 2 + 3)

(x 2 −1)4

(x 2 −1)3

Определим выпуклость и вогнутость кривой на промежутках.

-∞ < x < -

3 ,

y′′ < 0, кривая выпуклая;

- 3 < x < -1,

y′′ < 0, кривая выпуклая;

-1 < x < 0,

y′′ > 0, кривая вогнутая;

0 < x < 1,

y′′ < 0, кривая выпуклая;

1 < x <

3 ,

y′′ > 0, кривая вогнутая;

3 < x < ∞,

y′′ > 0, кривая вогнутая.

7. Про вертикальные асимптоты было уже сказано выше. Теперь

найдем наклонные асимптоты.

x 2

k = lim

= lim

= 1;

2 −1

x →∞ x

x →∞

−

x 2

− x

+ x

b = lim

= lim

= 0

−1

− x

= lim

−

x →∞ x

x →∞

x →∞ x

x →∞

−

x 2

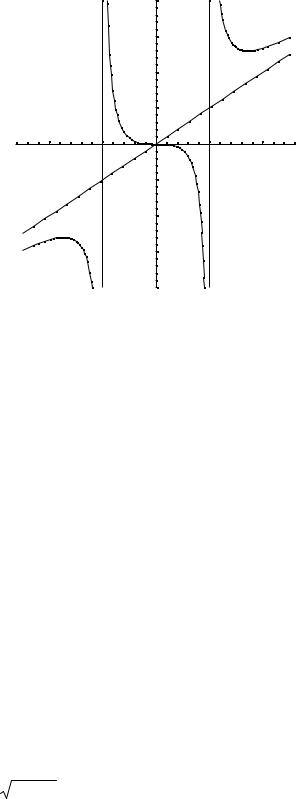
Итого, уравнение наклонной асимптоты y = x. 8. Построим график функции:

		4
		3
		2
		1
-2	-1	1	2
		-1
		-2
		-3
		-4

Рис. 16

9. Наибольшее и наименьшее значения функции на отрезке

Правила для нахождения наибольшего и наименьшего значения функции f (x ) на отрезке [a; b]:

1.Находим ООФ.

2.Проверяем, принадлежат ли [a; b] ООФ.

3.Находим критические точки.

4.Проверяем, принадлежат ли они [a; b].

5.Находим значения функции в критических точках, принадлежа- щих отрезку [a; b], и на концах f (x i ), f (a), f (b ).

6.Выбираем наибольшее и наименьшее значения.

Пример. Найти наибольшее и наименьшее значения функции

y = x 3	+ x 2	−6x + 5 на отрезке [0; 3].
3	2

Решение.

1.ООФ – все действительные числа;

2.[0; 3] ООФ;

3. Находим критические точки: y ′ = x 2 + x −6 ; x 2 + x −6 = 0 ;

x 1,2	=	−1 ± 1 + 24	;	x 1 = −3 ; x 2 = 2
x 1,2	=	2	;	x 1 = −3 ; x 2 = 2
		2
				98

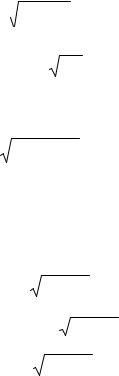
4. x 1 [0; 3],

x 2 [0; 3];

5. y (2)= −2

;

y (0)= 5 ;

y (3)=

1 .

Ответ: yнаиб = y (0)= 5 ;

yнаим

= y (2)= −2

Расчетные задания

Задача 11. Найти производные y x' .

11.1. y = ln sin(2x + 5);

y = x x ;

x2+y2=a2.

sin x

y 2

11.2. y = 4

;

y=x–x ;

= c

cos2 x

11.3. y = ctg2 2x ;

y=x2x;

xy=ex+y .

11.4. y = 3 tg2 3x ;

y=ln cos2x;

x+y=ey .

11.5.y=arccos x 3 ;

y=ln sinx2 ;

=ey/x.

11.6. y=exsin2x ;

y=ln tg2x;

y=cos(xy).

11.7 .y= 1 + tg2 x ;

y= (sinx)x;

xy=ln(1+y).

11.8. y=sin2(1+1/x);

y=(tgx)x;

=ln(xy).

11.9 .y=3tgx;

y=xcosx ;

x3+y3–3axy=0.

11.10 .y=tg 1 − x 2 ;

y=(sinx)lnx ;

x–y+a siny=0.

11.11.y=arcsin 1 − 3x ;

y=xcosx;

x2+y2+axy=0.

11.12.y=sin 1 − x 2 ;

y=(cosx)x ;

x2+ln(xy)=0 .

11.13.y=tg2(lnx);

y=xsinx;

x2+sin(xy)=0.

11.14. y=2cos3x;

y=(lnx)x;

x2+x sinx=0.

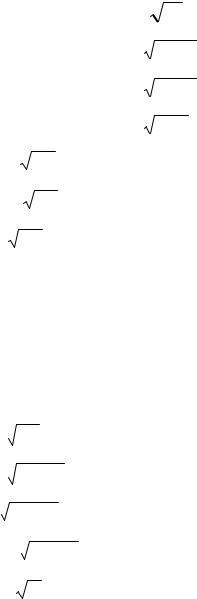
11.15. y= 3tg2x;			y= x x		;			y+exy=0.
11.16. y=2sin2x;			y= x sin x			;		y–2xy=0.
11.17. y=ln tg2x;			y= x cos x			;		y2–ln(xy)=0.
11.18. y=cos2e3x;			y= x ln x ;					x=ln(x+y).
11.19. y= arctg	2x ;		y=x–2x;					x+y=eу.

11.20. y=arcsin	3x ;		y=xlnx;					y=sin(xy).
11.21. y=ln tg 2x ;			y=x x 2 ;					y=cos(xy).

11.22. y=sin2x cos2x;			y= (sinx)–x;					y2+x=cos(xy).
11.23. y= sin 2x	;		y=(cosx)–x;					xy=ln(xy).
cos2 x
11.24. y= e2xsin ax;			y=(ctgx)x;					x+y2=tg(x+y).
11.25. y=e3xtg ax;			y= (tgx)–x;					yx2=exy.
11.26. y=sin3 4 x 3 ;			y=x3x;					y2=exy.
11.27. y=cos3 4 x +1 ;			y=x4x;					y2+sin(x+y)=0.
11.28. y=tg2 3 2x +1 ;			y=x5x;					y2+cos(x+y)=0.

11.29. y = ctg2 4	2x +1 ;		y=x–3x;					xy+cos(x+y)=0.

11.30. y=ln ctg	x ;		y=x–4x;					xy+sin(x+y)=0.
Задача 12. Найти производную второго порядка y xx'' для функции
заданной параметрически.
x = cos(t / 2);				3	+ 8t ;			x =t −sint ;
12.1.		12.2.	x =t	3			12.3.
12.1.		12.2.	x =t				12.3.
y =t −sint.			y =t 5 + 2t.					y = 1 − cost.

100

12.4.

;

12.5.

;

12.6.

= 3 cost ;

x = e

x = 3 cos

y = cost.

y = 2 sin3 t.

y = 4 sin

12.7.

12.8.

;

12.9.

x = ln cost ;

x = 3t −t ;

x = 2t −t

y = 3t 2 .

y =t 3 .

y = ln sint.

12.10.

x = lntgt ;

12.11.

= a cost ;

12.12.

= a cos

t ;

= lnctgt.

= b sint.

y = b sin3 t.

12.13.

x = lnt ;

12.14.

= 3 cost ;

12.15.

= 3 sint ;

= cost.

y =t.3

y =t 3 .

12.16.

= cos

t ;

12.17.

=t −1;

12.18.

x =t

;

y =t 2 .

y = 2t 3 .

=t 2 −1.

12.19.

= et ;

12.20.

x = sin 2t ;

12.21.

x = cos 2t ;

= lnt.

= cost.

= sin 2t.

12.22.

x = tgt ;

12.23.

x =t

;

12.24.

x = lnt ;

= ctgt

= sint.

=t 3 −t 2 .

x = cosat ;

12.26.

= a sin

t ;

12.27.

+1;

12.212.

y = sinat.

y = b cost 2 .

y =e 3t .

;

12.28.

sint

12.29.

cost

12.30.

sint

= cos

y = tgt.

y = ctgt.

Задача 13. Составить уравнения касательной и нормали к данной кривой в точке с абсциссой x0.

13.1. y=3x2+x+1;	x0= –2.	13.2. y= 5x2–4x+3;	x0= 1.
13.3. y= 2x2 –5x +7;	x0=2 .	13.4. y= 4x2 –5x–11;	x0= 3.

101

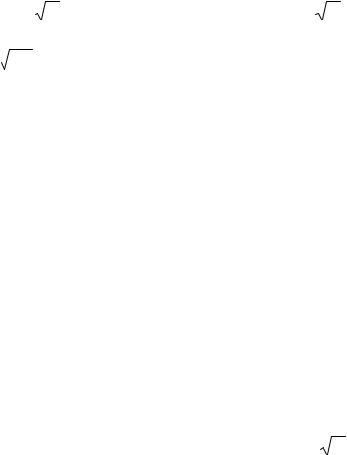
13.5. y=

3x −1

;

x0= 2 .

13.6. y=

2x + 3

;

x0= 1.

x 2 − 4

x 2 −1

13.7. y=

x −5

;

x0= –3.

13.8. y=

5x − 4

;

x0= –1.

x 2 −7

x 2 − 2

13.9. y= 3x+

;

x0= –2 .

13.10. y=5x+

;

x0= 1.

;

13.12. y= 3x3+

;

13.11. y= 7x2+

x0= –1.

x0= –2.

x 2

13.13. y= 2x2–6

x –44;

x0= 9 .

13.14. y=3x2+4

x –40 ;

x0= 4.

13.15. y= 3 3 x 2 –10;

x0= 8.

13.16. y= x 3 − 2x 2 + 4 ;

x0= 1.

x 2 − 4

13.17. y=

2x 3 −x

;

x0= –1.

13.18. y=

2x 3

;

x0= 2.

x 2 −5

x 2 −x + 4

13.19. y= 7x2 +6x –12;

x0= –2.

13.20. y= 2x2 –4x –3;

x0=3.

13.21. y=x2 –7x +8;

x0= 4.

13.22. y=

2x 2 –1;

x0= –3.

13.23. y= x 3 –x+1;

x0=1.

13.24. y=

x 3 –x–2;

x0= –1.

13.25. y=

;

x0= 1 .

13.26. y=

;

x0= 3.

3x −1

2x −1

13.27. y=

;

x0= 2.

13.28. y=

–3;

x0= 1.

3x − 2

13.29. y= 2x–3x2;

x0= –1 .

13.30. y= 4x2+5

x +3;

x0= 1.

Задача 14. Вычислить приближенно с помощью дифференциала.

14.1 .tg4503’.

14.2. ctg 4503’.

14.3. arctg1,02.

14.4. arctg0,97.

14.5. sin 6003’.

14.6. sin 59057’.

102

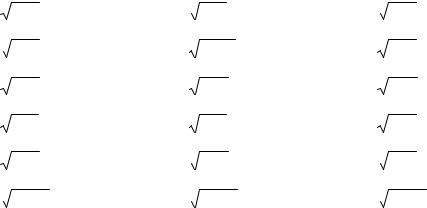
14.7. ln 0,995.		14.8. ln 1,005.		14.9. arctg0,98.

14.10. sin 3001’.		14.11. sin 29059’.		14.12. cos 59057’.
14.13.	902 .	14.14. 4	126 .	14.15. 4	624 .

14.16. 4	626 .	14.17. 3	1330 .	14.18.3	730 .

14.19. 3	728 .	14.20. 3	215 .	14.21.3	217 .

14.22. 3	513 .	14.23. 3	511 .	14.24.3	344 .

14.25. 3	342 .	14.26. 4	257 .	14.27. 4	255 .

14.28. 4	4087 .	14.29. 4	4085 .	14.30. 4	2402 .

Задача 15. Вычислить, применяя правило Лопиталя.

15.1. lim(sin x )tgx			1	x	15.21. lim(1 − cos2 x )sin 3x
x →0	15.11. lim arctg				x →0
x →0	15.11. lim arctg		x		x →0
	x →0		x
15.2. lim(1 − cos x )sin2 x	15.12. lim(sin x )x 2				15.22. lim(e x − cos x )x
x →0	x →0				x →0
15.3. lim(arcsin x )x	15.13. lim(1 − cos 2x )tgx				15.23. lim(ln(1 + x 2 ))sin x
x →0	x →0				x →0
15.4. lim(ln(1 + x ))sin x	15.14. lim(arctgx )sin 2x				15.24. lim(sin 3x )arcsin x
x →0	x →0				x →0
15.5. lim(sin x )3x	15.15. lim(3x )1−cos x				15.25. lim(arctgx 2 )ex −1
x →0	x →0				x →0
15.6. lim(arctgx )tgx	15.16. lim(e x	−1)sin 3x			15.26. lim(sin 3x )x +tgx
x →0	x →0				x →0
15.7. lim(ln(1 − 2x ))sin2 x	15.17. lim(ln(1 + x 2 ))x				15.27. lim(arcsin x )1−cos x
x →0	x →0				x →0
15.8. lim(tgx )arcsin 2x	15.18. lim(x 2 + x )sin x				15.28. lim(1 + x + x 2 )x
x →0	x →0				x →0
15.9. lim(x sin x )1−cos x	15.19. lim(tgx 2 )x 3				15.29. lim(x 3 )sin 5x
x →0	x →0				x →0
15.10. lim(x 2 )sin 3x	15.20. lim(x 2 + x + 1)arcsin x				15.30. lim(ln(1 − x ))arctgx
x →0	x →0				x →0

Задача 16. Провести полное исследование функции и построить ее график.

103

<<< < Предыдущая 1 2 3 4 5 6 7 8 910 / 1110 11 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
11.03.201649.15 Кб442Макшеев. Система органов государственной власти в РФ..doc
#
28.03.201561.86 Кб30Маркетинг.docx
#
27.03.2015469.5 Кб34маркитанов кр.doc
#
28.03.20152.57 Mб44Мат. логика.pdf
#
21.04.2019229.24 Кб33матан.docx
#
28.03.2015767.71 Кб41Математика, теория+расчетные 1 семестр.pdf
#
28.03.201516.93 Mб31Математика1.pdf
#
15.08.2019215.2 Кб16матер_лаба1_теория.docx
#
28.03.2015138.99 Кб50Материал для отчета по практике.docx
#
28.03.20154.34 Mб34Материал по экологии.djvu
#
27.03.201598.3 Кб37материаловедение №3 вариант №19 .doc