Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Нижегородский Государственный Технический Университет им. Р.Е. Алексеева

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Математика, теория+расчетные 1 семестр

.pdf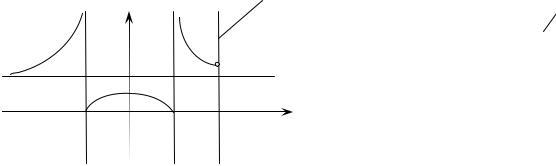

Скачиваний:

Добавлен:

28.03.2015

Размер:

767.71 Кб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 89 / 119 10 11 > Следующая >>>

Задача 10. Найти точки разрыва функции и исследовать их ха-

, x < 2 .

x2 −1

рактер y= 2

≥ 2

x, x

Решение. Функция не существует в точках x=±1. Рассмотрим одно-

сторонние пределы: lim

y = 0 ,

lim y = ∞ , так как y = 2

–

функция

x 2 −1

→1−0

x →1+0

четная, то

lim

y = 0 ,

lim y = ∞,

x →−1+0

x →−1−0

а lim y = 2 , lim y = 2 13

≈ 1,26 .

x →2+0

x →2

−0

точках

Следовательно,

x=±1 – разрыв второго рода, а в

точке x=2 – разрыв первого рода.

−1

lim 2

= 1 , сле-

Зная,

что

x 2 −1

x →∞

Рис. 15

дует построить схематически гра-

фик этой функции (рис. 15).

V. Дифференциальное исчисление функции одной переменной

Теория

1. Производная функции, основные правила дифференцирования

Определение. Производной функции f(x) в точке х = х0 называется предел отношения приращения функции в этой точке к приращению ар- гумента, если он существует.

′	f (x + x ) − f (x )	.
f (x ) = lim	x	.
x →0	x

Основные правила дифференцирования. Обозначим f(x) = u, g(x) = v- функции, дифференцируемые в точке х.

1)(u ± v)′= u′± v′;

2)(u v)′ = u v′ + u′v;

3)u ′ = u′v − v′u , если v ≠ 0.v v2

Производные основных элементарных функций.

С′ = 0

9) (sin x )′ = cosx

(xm)′ = mxm-1

10) (cosx )′ = −sin x

(

x )′ =

11) (tg x )′ =

cos2 x

′

= −

12) (ctg x ) = − sin2 x

(e x )′ =e x

13) (arcsin x )′ =

1 − x 2

(ax )′ = ax lna

14) (arccosx )′ = −

−x 2

′

7)(ln x )

15) (arctgx )

1 + x 2

(loga x )′ =

16) (arcctgx )′ = −

x lna

1 + x 2

Пример. y

x 2 +

′

(x 2 + x )′tgx − (x 2 + x )(tgx

)′

′

tgx

tgx − (x

x )

cos2 x

tg2x

Производная сложной функции

Теорема. Пусть y = f(x); u = g(x), причем область значений функ- ции u входит в область определения функции f.

y ′ = f ′(u ) u′, т. е. сначала вычисляется производная функции f (u ) по переменной u , и затем она умножается на производную функции u(x ) по переменной x .

Пример. Найти производную функции y = lntg

x −

sin x

sin x − x cos x

′

sin x − x cos x

cos

2 x

2 −

sin2 x

2 sin

cos

x −

sin2

= sin x −sin x + x cos x = x cos x

sin2 x

2. Производная показательно-степенной и неявно заданной функ- ции

Определение. Функция называется показательной, если незави- симая переменная входит в показатель степени, и степенной, если пере- менная является основанием. Если же и основание и показатель степени зависят от переменной, то такая функция будет показательно-степенной.

Пусть u = f(x) и v = g(x) – функции, имеющие производные в точке х, f(x)>0.

Найдем производную функции y = uv. Логарифмируя, получим: lny = vlnu

	y ′		′		u′
	y =v		′	lnu +v u
	y =v			lnu +v u
y ′ =u		v		u′
y ′ =u		v		u	+v ′lnu
				u

Пример. Найти производную функции y = (arcsinx ) x +2 . Решение. Логарифмируем функцию y :

ln y = ( x + 2 )ln (arcsin x ).

Дифференцируем это равенство по x :

y ′

′

= [(

x + 2 )ln (arcsin

x )]

= ( x

+ 2 ) ln arcsin

+ ( x

+ 2 )(ln(arcsi

n x ))

′

ln (arcsin

x )+ (

+ 2 )×

(arcsin

x )′ =

ln(arcsin

x ) + (

x + 2 ) ×

2 x

arcsin

. .

1 − x 2 arcsin x

ln(arcsin x )

Получим: y ′ = (arcsin x )

x + 2

1 − x 2

arcsin x

Производная неявных функций

Если

функция

y = f (x )

такова,

что

подстановке ее

уравнение

F (x , y )= 0 , последнее обращается в тождество, то говорят о неявном за-

дании функции y = f (x ).

Пусть дифференцируемая функция y = f (x )

задана уравнением F (x , y )= 0 . Тогда дифференцируем левую и правую

часть уравнения, считая y сложной функцией, и выражаем из уравне-

ния y ′.

Пример. Найти производную функции sin x

+ x 3

= exy + y 2 .

′

Решение.

+ x

+ y

′

x ′

′

xy ′

+ (y

′

sin

= (e

);

sin

+ (x

) =

)

′

− xy

′

− xy

′

x y

Так как sin

cos

= cos

y 2

(e xy )′ = e xy (y + xy ′), (x 3 )′ = 3x 2 , (y 2 )′ = 2yy ′,

то

x y − xy

′

′)+ 2yy ′.

cos

+ 3x

+ xy

y 2

содержащие y ′,

переносим в левую часть, а все осталь-

Слагаемые,

ное в правую:

′ x

cos

+ xe

+ 2y

cos

− ye


	1	cos x		+ 3x 2 − ye xy
		cos x		+ 3x 2 − ye xy
y ′ =	y		y				.
y ′ =	x		cos x		+ xe xy	+ 2y
	y 2		cos x		+ xe xy	+ 2y
	y 2		y

3. Производные высших порядков. Производная параметрически заданной функции

Пусть функция f(x) дифференцируема на некотором интервале. То- гда, дифференцируя ее, получаем первую производную

y ′ = f ′(x ) = dfdx(x ) .

Если найти производную функции f′(x), получим вторую производ- ную функции f(x):

					y	′′	′′	d 2f (x )	,
					y		= f (x ) =	dx 2	,
т.е. y′′ = (y′)′ или	d 2 y			d	dy
	dx 2	=					.
		=					.
			dx dx

Этот процесс можно продолжить и далее, находя производные сте- пени n:

d	n	y			d		n	−1	y
						d
		n	=							.
dx								n −1
				dx dx

Общие правила нахождения высших производных Если функции u = f(x) и v = g(x) дифференцируемы, то:

1)(Сu)(n) = Cu(n);

2)(u ± v)(n) = u(n) ± v(n);

3) (u v )(n ) =vu(n ) + nu(n −1)v ′ + n(n − ...1)u(n −2)v ′′ + + n(n −1)...[n −(k −1)]u(n −k )v (k ) +...
2!	k!

... +uv (n ) .

Это выражение называется формулой Лейбница.

Пример. Найти d 2 y функции y = arcsine x . dx 2

Решение.

′

x ′

e x

y ′

= dx = (arcsine

) =

1 −e 2x

′

x ′

2 x

− e

( 1 − e

2 x

′

) 1 − e

)

2 x

1 − e

2 x

1 − e

ex 1 − e2 x + ex

e2 x

1 − e2 x

− e2 x )2

Дифференцирование функции, заданной параметрически.

Задание функции

y = f (x )

через x = ϕ(t ), где t [t1;t2 ] − параметр,

y = ψ(t )

называется параметрическим.

Если функции x = ϕ(t ) , y = ψ(t ) имеют

′

производные ϕ (t )≠ 0 и

ψ (t ), то функция y = f (x ) также имеет произ-

водную, вычисляемую по формуле

ψ (t )

′

dx = y x′ =

ϕ′(t )

xt′

Вторая производная вычисляется по формуле

d 2 y

= y ′/ xx =

(y x′ )t/

dx 2

xt′

Пример. Функция y задана параметрически: x = cos4t ,

′

′′

y = 2 lnt

0 <t < +∞. Найти y x

и y xx .

Решение. Найдем xt′ = ϕ′(t )= (cos 4t )′

= (−sin 4t ) 4

yt′ = ψ′(t )=

(2 lnt )′ =

Тогда по формуле

y x′ =

− 4 sin 4t

− 2t sin 4t

(t sin 4t )/

Для вычисления y′′xx найдем (y x′ )

(t sin 4t )2

2t sin 4t

(sin 4t +t 4 cos4t )

−

= 1

t 2 sin2 4t

Тогда,

(y x′

)t/

d 2 y

′

sin4t +4t cos4t

sin 4t + 4t cos4t

dx 2

= y xx

xt′

2 sin2 4t (−4 sin4t )

= −

8t 2 sin3 4t

4. Дифференциал функции

Пусть функция y = f(x) имеет производную в точке х:

lim

′

= f (x ).

x →0

′

Тогда можно записать:

x = f

+ α, где α→0, при

х→0.

(x )

Следовательно:

y = f

′

x .

(x ) x + α

Величина αΔx − бесконечно малая более высокого порядка, чем

f′(x)

x, т.е. f′(x)

x – главная часть приращения у.

Определение. Дифференциалом функции f(x) в точке х называет-

ся главная линейная часть приращения функции.

Обозначается dy или df(x).

Из определения следует, что dy = f′(x)

x или dy = f′(x)dx.

′

= dx

Можно также записать: f (x )

Для приближенного вычисления очевидно справедлива формула f (x 0+ x)= f(x0)+f ’(x0) x.

Пример. Вычислить приближенно с помощью дифференциала ln 0,97.

Решение. В данном случае x0=1, x= −0,03 и

ln(x+ x)=ln(x0)+(1/x0) x, и поэтому ln 0,97=ln1+(1/1)(−0,03).

Геометрический смысл дифференциала Дифференциал функции f(x) в точке х равен приращению ордина-

ты касательной к графику этой функции в рассматриваемой точке.

Свойства дифференциала

Если u = f(x) и v = g(x)− функции, дифференцируемые в точке х, то непосредственно из определения дифференциала следуют следующие свойства:

1) d(u ± v) = (u ± v)′dx = u′dx ± v′dx = du ± dv; 2) d(uv) = (uv)′dx = (u′v + v′u)dx = vdu + udv; 3) d(Cu) = Cdu;

4)	d	u	=	vdu −udv	.
		v		v 2

По формуле dny = f(n)(x)dxn может быть найден дифференциал n-го порядка.

Уравнение касательной к нормали Угол между кривыми может быть определен как угол между каса-

тельными, проведенными к этим кривым в какой- либо точке.

Уравнение касательной к кривой: y − y 0					= f	′
						(x 0 )(x − x 0 )
Уравнение нормали к кривой: y − y 0 = −					1		(x − x 0 ).
					′
					f (x 0 )
Пример. Составите уравнение касательной и нормали к кривой
f (x )= −x 2 − 4x в точке x 0	= −1 .
Решение. f (− 1)= −(− 1)2 − 4(− 1)= −1 + 4 = 3
′		′
f (x )= −2x −4 ,		f (− 1)= −2(− 1)− 4 = 2 − 4 = −2 .
Уравнение касательной:		y − 3 = −2(x + 1)			y = −2x + 1.
Уравнение нормали:	y − 3 =		1	(x +1);	y = 0,5x + 3,5 .

		2

5.Раскрытие неопределенностей. Правило Лопиталя

Кразряду неопределенностей, как указывалось ранее, относятся следующие соотношения:

00 ; ∞∞; ∞ 0; ∞0 ; 1∞; ∞ − ∞.

Теорема (правило Лопиталя). Если функции f(x) и g(x) диффе- ренцируемы в вблизи точки а, непрерывны в точке а, g′(x) отлична от нуля вблизи а и f(a) = g(a) = 0, то предел отношения функций при х→а равен пределу отношения их производных, если этот предел (конечный или бесконечный) существует.

lim f (x )			= lim f		′
					(x ) .
	g (x )				′
x →a			x →a	g (x )

Пример: Найти предел lim		x 2 −1 + ln x			.

x →1		e x −e

При попытке непосредственного вычисления предела получается неопределенность вида 00 . Функции, входящие в числитель и знамена-

тель дроби, удовлетворяют требованиям теоремы Лопиталя.

′

2x +

2 +1

f′(x) = 2x +

;

g′(x) = ex;

lim f

(x )

′

x →1

Пример. Найти lim

e x

x →+∞ x 2

∞

Решение.

. Применяем

Здесь имеет место неопределенность

правило Лопиталя:

∞

(e x

)′

(e x )′

lim

e x

∞

= lim

lim

e x

∞

= lim

e x

= ∞.

x →+∞ x 2

∞

x →+∞ (x 2 )′

x →+∞ 2x

∞

x →+∞ (2x )′

x →+∞

Если при решении примера после применения правила Лопиталя попытка вычислить предел опять приводит к неопределенности, то пра- вило Лопиталя может быть применено повторно. Естественно, это воз- можно только в том случае, если вновь полученные функции в свою оче- редь удовлетворяют требованиям теоремы Лопиталя.

Следует отметить, что правило Лопиталя – всего лишь один из спо- собов вычисления пределов. Часто в конкретном примере наряду с пра- вилом Лопиталя может быть использован и один из разобранных выше методов (замена переменных, домножение и др.).

Неопределенности вида 00 ; 1∞; ∞0 можно раскрыть с помощью логарифмирования. Такие неопределенности встречаются при нахожде- нии пределов функций вида y = [f (x )]g (x ) , f(x)>0 вблизи точки а при

х→а. Для нахождения предела такой функции достаточно найти предел функции lny = g(x)lnf(x).

Пример. Найти предел lim x x .

x →0

Здесь y = xx, lny = xlnx.

x >0

Тогда

правило

lim ln y = limx ln x = lim ln x

= lim

1/ x

= −lim x = 0

− 1/ x 2

x →0

Лопиталя

x →0

x >0

Следовательно lim ln y = ln lim y = 0; lim y = lim x x = 1.

x →0

→0

x >0

6. Исследование функций с помощью производной. Возрастание и убывание функций

Теорема. 1. Если функция f(x) имеет производную на отрезке [a, b] и возрастает на этом отрезке, то ее производная на этом отрезке неотри- цательна, т.е. f′(x) ≥ 0.

2. Если функция f(x) непрерывна на отрезке [a, b] и дифференци- руема на промежутке (а, b), причем f′(x) > 0 для a < x < b, то эта функция возрастает на отрезке [a, b].

Аналогично можно сделать вывод о том, что если функция f(x) убы- вает на отрезке [a, b], то f′(x)≤0 на этом отрезке. Если f′(x)<0 в промежутке (a, b), то f(x) убывает на отрезке [a, b].

Конечно, данное утверждение справедливо, если функция f(x) не- прерывна на отрезке [a, b] и дифференцируема на интервале (a, b).

Определение. Функция f(x) имеет в точке х1 максимум, если ее

значение в этой точке больше значений во всех точках некоторого интер- вала, содержащего точку х1. Функция f(x) имеет в точке х2 минимум, если f(x2 + x) > f(x2) при любом х ( х может быть и отрицательным).

Очевидно, что функция, определенная на отрезке может иметь мак- симум и минимум только в точках, находящихся внутри этого отрезка. Нельзя также путать максимум и минимум функции с ее наибольшим и

<<< < Предыдущая 1 2 3 4 5 6 7 89 / 119 10 11 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
11.03.201649.15 Кб442Макшеев. Система органов государственной власти в РФ..doc
#
28.03.201561.86 Кб30Маркетинг.docx
#
27.03.2015469.5 Кб34маркитанов кр.doc
#
28.03.20152.57 Mб44Мат. логика.pdf
#
21.04.2019229.24 Кб33матан.docx
#
28.03.2015767.71 Кб41Математика, теория+расчетные 1 семестр.pdf
#
28.03.201516.93 Mб31Математика1.pdf
#
15.08.2019215.2 Кб16матер_лаба1_теория.docx
#
28.03.2015138.99 Кб50Материал для отчета по практике.docx
#
28.03.20154.34 Mб34Материал по экологии.djvu
#
27.03.201598.3 Кб37материаловедение №3 вариант №19 .doc