Математика, теория+расчетные 1 семестр

Задача 7. Построить кривую в полярных координатах.

65

2. Угол между ребрами А1А2 и А1А4 определим как угол между век-

Замечание. Объем параллелепипеда равен модулю смешанного произведения векторов, на которых он построен, как на сторонах. Знак + или – характеризует ориентацию тройки векторов в заданной системе координат.

5. Уравнение прямой А1А4 запишем в канонической форме x −mx0 = y −n y0 = z −pz0 , где s = (m, n, p) – направляющий вектор прямой,

А(x0,y0,z0) – точка на этой прямой.

6. Уравнение плоскости, проходящей через три данные точки, опре-

деляем по формуле (A1M , A1 A2 , A1 A3 )= 0 , где М(x,y,z) – текущая точка плоскости, или

67

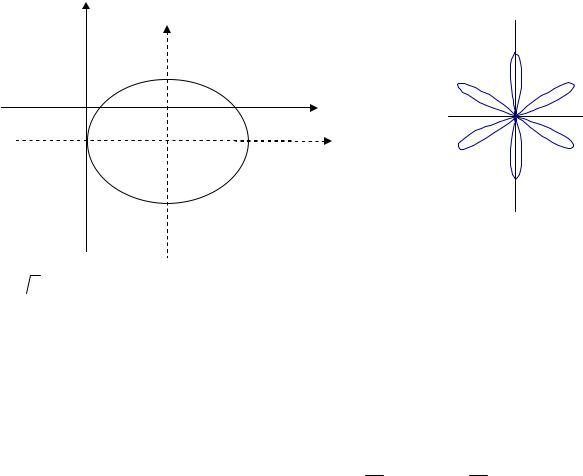
Следовательно, исходное уравнение определяет эллипс с центром в точке (3,–1). Оси этого эллипса параллельны осям координат a=3,

b= 5 (рис. 12).

Задача 6 решается аналогично.

Задача 7. Построить кривую в полярных координатах: ρ=cos(6ϕ –

3π).

Решение. Построим сначала график ρ=cos 6ϕ. Это 6-лепестковая роза, вписанная в единичную окружность. Найдем точки лежащие на окружности, решая уравнение cos 6ϕ=1 ϕ = πk/3, и границы лепестков, решая уравнение

cos 6ϕ ≥0 − π2 + πk ≤ 6ϕ ≤ π2 + πk −12π + π6k ≤ϕ ≤ 12π + π6k .

Так как ρ=cos(6(ϕ –π/2)), то исходная линия получается из базовой поворотом на угол π/2 против часовой стрелки (рис. 13).

69

IV. Предел последовательности и функции одной переменной

Теория

1. Предел числовой последовательности

Определение. Последовательностью называется функция нату- рального аргумента. Значения такой функции называются элементами последовательности и обозначаются обычными строчными латинскими буквами {an } = a1 , a2 ,..., an−1 , an , an+1 ,... , причем an ≡ f (n) − функция натураль- ного аргумента.

Индекс показывает, какой номер имеет данный элемент, то есть ка- кому натуральному числу он соответствует. Каждому натуральному чис- лу n, таким образом, соответствует элемент с номером n.

Примеры:

1){an } , где an = a1 + d (n −1) ~ a1 , a1 + d, a1 + 2d,..., a1 + d (n −1),...

2){an } , где an = a1 qn−1 ~ a1 , a1q, a1q2 ,...,a1qn−1 ,...

Определение. Число a называется пределом последовательности {an } , если, начиная с некоторого номера, все ее элементы попадают в

сколь угодно малую ε – окрестность точки a .

Другими словами, каково бы ни было ε>0, найдется номер N, такой,

точки a находится разве что конечное число элементов последовательно- сти {an } .

Определение. Если lim n → ∞ {an } = a (a − конечное число), то гово- рят, что {an } сходится к числу a (или имеет предел a ). Сама последова- тельность в этом случае называется сходящейся.

Если limn →∞ {an } = ∞ или не существует, то говорят, что {an } расхо- дится. Символом ∞обозначается бесконечно большое число

70

Теорема. Если последовательность {an } имеет конечный предел ( a < ∞), то он единственный (или: сходящаяся последовательность имеет

лишь один предел).

Определение. Последовательность называют ограниченной, если существует такое число М>0, что для всех n выполняется неравенство an M , то есть все элементы последовательности лежат в интерва-

ле (−М;М)

Утверждение. Если последовательность имеет предел, то она ог- раничена.

Арифметические свойства сходящихся последовательно- стей.

Пусть {an } и {bn } сходящиеся последовательности, т.е. limn →∞ an = a

иlimn→∞ bn = b . Тогда:

1)limn →∞(an ±bn ) = limn →∞ an ± limn →∞ bn =a ±b ;

2)limn →∞(an bn ) = limn →∞ an limn →∞ bn = ab ;

3)limn →∞(an ) = limn →∞ an = a , limn →∞ bn ≠ 0, n ;

bn limn →∞ bn b

4)limn →∞(Can ) =C limn →∞ an , С – const;

5)limn →∞(1 + n1 )n = e ≈ 2,718281828459045 …, е – трансцендентное чис-

ло.

2. Бесконечно малые и бесконечно большие числовые последова- тельности

Определение. {αn } называется бесконечно малой (б.м.) числовой последовательностью при n → ∞, если limn→∞ αn = 0 :

ε > 0 N (ε) ≥ 0, n > N (ε) γn > ε.

71

Если при этом все элементы последовательности, начиная с некото- рого номера, остаются положительными, говорят, что последовательность сходится к «плюс бесконечности»: limn →∞ γn = +∞ , а если отрицательны-

ми – то к «минус бесконечности»: limn →∞ γn = −∞ Заметим, что:

Имеют место следующие свойства б.м. числовых последовательно-

стей:

1)Сумма конечного числа б.м. {} – б.м. {};

2)Произведение б.м. {} на ограниченную {} - б.м. {};

3)Произведение конечного числа б.м. {} – б.м. числовая {}. Замечание 1. Отношение двух б. м. ничего определенного не дает. В этом слу-

чае говорят, что имеет место неопределенность вида 00 .

2. У рациональной дроби, представляющей отношение двух много- членов степеней n и m соответственно (m,n N ), и числитель и знамена- тель стремятся к бесконечности. Говорят, что имеет место неопределен-

ность вида ∞∞ .

3. Предел функции.

Понятие предела функции по Коши или на “языке “ (ε,δ) (рис.

14).

72

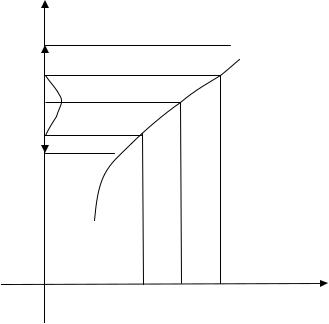
Y

A+ε

A

A–ε

limx →x0 +0 f (x ) =C ≡ f (x 0 +0).

С – правый предел f(x) или x → x 0 +0 .

Определение предела функции по Гейне. Число А называют

пределом функции f(x) в точке x 0 , если:

1)функция определена в некоторой окрестности точки, кроме, быть может, самой этой точки;

2)для любой последовательности x n → x 0 (x n ≠ x 0 при всех n) по-

следовательность значений y n = f (x n ) = сходится к А. Записывают

limx →x0 f (x ) = A .

В предыдущем пункте рассматривалось определение бесконечного предела последовательности. Определение предела функции позволяет без труда ввести такие понятия, как предел f(x) приx → ∞ (через после-

73