Математика, теория+расчетные 1 семестр

а2=b2 .

Свойства гиперболы

1.Гипербола является симметричной кривой относительно осей коорди- нат. Ось симметрии, проходящая через фокусы, называется фокальной осью, а точка пересечения осей симметрии – центром гиперболы.

2.Гипербола пересекает ось Oх в точках А1(-а,0) и А2(а,0).

3.Отрезок А1А2 называется действительной осью гиперболы (фокальная ось).

4.Прямые у=(b/a)x и y=(–b/a)x, содержащие диагонали прямоугольника с вершинами N1(–a,–b), N2(–a,b), N3(a,b), N4(a,–b), являются асимптотами

гиперболы.

5.Величина ε=с/а называется эксцентриситетом гиперболы. Так как для гиперболы справедливо неравенство с>а , то эксцентриситет гиперболы удовлетворяет условию ε>1.

Геометрический смыл эксцентриситета: большему значению ε соот- ветствует гипербола более сжатая вдоль фокальной оси.

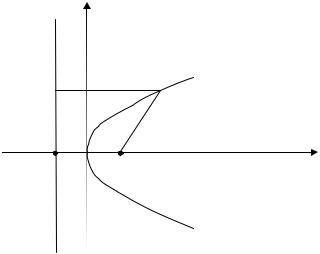
Парабола Определение. Параболой (рис. 8)называется геометрическое место

точек плоскости, равноудаленных от данной точки F, называемой фоку- сом, и данной прямой l, называемой директрисой.

44

Y

d M(x,y) k

l

Рис. 8

Каноническое уравнение параболы имеет вид у2=2рх, где р – рас- стояние от фокуса до директрисы.

Свойства параболы.

1.Парабола не имеет центра симметрии.

2.Парабола симметрична относительно оси 0х.

3.Точка (0,0) пересечения параболы с осями координат называется вершиной параболы.

4.За эксцентриситет параболы принимают отношение расстояний от произвольной точки М параболы до директрисы – d и до фокуса – r, то

есть ε=d/r = 1, т.к. r = d.

Замечание. Эллипс и гипербола имеют центр симметрии и поэто- му называются центральными, а парабола не имеет центра симметрии − нецентральная кривая.

Следует отметить, что указанные кривые могут быть получены как сечения прямой круговой конической поверхности плоскостью (рис. 9):

1.Если секущая плоскость α перпендикулярна оси АВ, то в сечении получим окружность.

2.Если секущая плоскость α составляет с осью АВ угол γ (β;π/2), то в сечении получим эллипс.

3.Если секущая плоскость α параллельна оси АВ и не проходит через вершину O , то в сечении получим гиперболу.

45

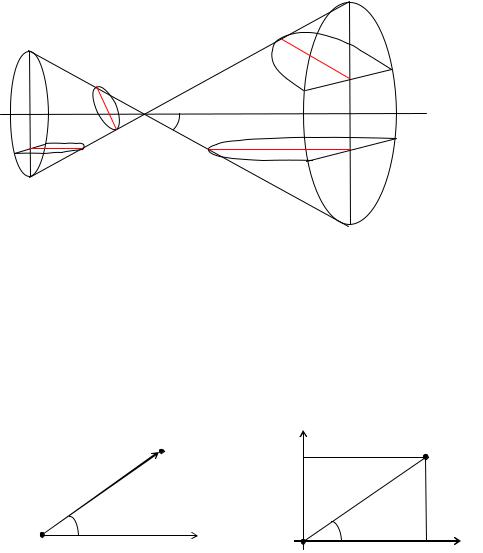
4.Если секущая плоскость α параллельная образующей CD и не про-

D

окружность

Рис. 9

ходит через вершину 0 , то в сечении получим параболу. 4. Полярная система координат

Для введения полярной системы координат на плоскости возьмем точку О плоскости и назовем ее полюсом. Из этой точки О проведем луч Ор, называемый полярной осью.

Рис. 10

Для произвольной точки М плоскости (рис. 10, а) однозначно опре- деляется длина отрезка ОМ, называемого полярным радиусом точки М, и которая обозначается символом ρ (заметим, что ρ= |ОМ| ≥ 0). Угол ϕ = МOр называется полярным углом точки М. Полярный угол рассматри- вают в пределах одного оборота и, как в тригонометрии, поворот против часовой стрелки считают положительным, а по часовой стрелке – отрица- тельным.

46

Если точка М имеет полярный радиус ρ и полярный угол ϕ, то это записывается в виде М(ρ,ϕ).

Определение. Упорядоченная пара действительных чисел

(ρ,ϕ) называется полярными координатами точки М. Полярной системой координат на плоскости называется полюс и полярный луч вместе с по- нятием полярных координат любой точки плоскости.

Замечание. Полярные координаты однозначно определяют поло- жение любой точки на плоскости, за единственным исключением – само- го полюса. Чтобы восстановить однозначность для любой точки плоскости полагают полярные координаты полюса равными нулю: О(0,0).

Определение. Говорят, что прямоугольная декартова система ко- ординат на плоскости Оху стандартным образом совмещена с полярной системой координат этой же плоскости, если полюс полярной системы ко- ординат совпадает с началом координат ПДСК, а полярный луч совпа- дает с положительным направлением оси абсцисс (рис. 10, б).

Теорема. Пусть прямоугольная декартова система координат на плоскости Оху стандартным образом совмещена с полярной системой ко- ординат на этой же плоскости. Тогда декартовые координаты (х,у) любой точки плоскости связаны с её полярными координатами (ρ, ϕ ) следую-

Приведем некоторые уравнения в полярной системе координат, описывающие известные геометрические места плоскости:

ρ sin ϕ = a уравнение прямой линии, отстоящей от поляры на

Пример. Построить кривую ρ = a cos 2ϕ. Решение.

47

Будем давать значения полярному углу ϕ от ϕ=0 до ϕ=2π через про- межуток α = 8π и вычислим соответствующие значения ρ. Найденные

значения поместим в табл.1. Примем произвольный отрезок за единицу масштаба, которой будем пользоваться при построении ρ. По значениям ρ и ϕ из таблицы построим точки, соответствующие каждой паре чисел ρ и ϕ, и соединим их плавной кривой.

Таблица 1

Построение кривой показано рисунке. Полученная кривая называ- ется четырехлепестковой розой (рис. 11).

48

Рис. 11

5. Плоскость в пространстве. Уравнения плоскости

Теорема. Уравнение плоскости П, проходящей через заданную точку M 0 (x0 , y0 , z0 ) Π и имеющей заданный вектор нормали

n = ( A, B,C) (≠ 0) , имеет вид

A(x − x0 ) + B( y − y0 ) + C(z − z0 ) = 0, A2 + B2 + C 2 ≠ 0 .

Преобразуем уравнение Ax + By +Cz −( Ax + By +Cz ) = 0 .

140 4204430

D

Тогда Ax + By + Cz + D = 0 – общее уравнение плоскости.

Теорема. Уравнением плоскости, проходящей через три точки

M1 (x1, y1, z1 ) , M 2 (x2 , y2 , z2 ) , M 3 (x3 , y3 , z3 ) , не лежащие на одной прямой, имеет вид

По аналогии с прямой на плоскости, уравнение плоскости, пересе- кающей координатные оси в точках (a,0,0) , (0,b,0) и (0,0,c) , имеет вид

ax + by + cz =1

и называется уравнением плоскости «в отрезках».

49

Обозначим через p расстояние от начала координат до плоскости Π , а через n0 = (cosα,cosβ,cos γ) единичный вектор нормали к этой плос-

кости.

Теорема. Точка M (x, y, z) лежит на плоскости Π тогда и только тогда, когда координаты этой точки удовлетворяют уравнению

x cos α + y cosβ + z cos γ − p = 0 .

Последнее уравнение называется нормальным (нормированным) уравнением плоскости.

Теорема. Пусть уравнения А1х+В1у+С1z+D1=0 и А2х+В2у+С2z+D2=0 определяют две плоскости α и β. Тогда:

1) угол ϕ между плоскостями α и β (линейный угол ϕ двугранного угла,

6. Прямая в пространстве

Теорема. Уравнения прямой в пространстве L, проходящей через точку M 0 (x0 , y0 , z0 ) L с направляющим вектором l = (m, n, p) , l ≠ 0 , име-

Уравнения называются каноническими уравнениями прямой.

Если обозначить x −mx0 = y −ny0 = z −pz0 = t , то получим

50

x = x0 + mt,

y = y0 + nt, t R – параметрические уравнения прямой.

z = z0 + pt,

Теорема. Пусть заданы две плоскости Π1 : A1x + B1 y + C1z + D1 = 0 ,

Π2 : A2 x + B2 y + C2 z + D2 = 0 . Если нормальные векторы n1 = ( A1, B1,C1 ) и n2 = ( A2 , B2 ,C2 ) неколлинеарны, тогда система уравнений

A1x + B1 y + C1z + D1 = 0,A2 x + B2 y + C2 z + D2 = 0

определяет прямую, по которой они пересекаются.

7. Взаимное расположение прямой и плоскости Теорема. Пусть задана плоскость α: Ax + By + Cz + D = 0 и прямая

линия l, каноническое уравнение которой имеет вид х−mх0 = y −n y0 = z −pz0 .

Тогда:

1) угол ϕ между прямой l и плоскостью α (это угол, образованный прямой l и ее проекцией l ′ на эту плоскость) определяется с помощью формулы

2)условие параллельности прямой l и плоскости α: Am + Bn +Cp = 0 ;

3)условие перпендикулярности прямой l и плоскости α имеет вид

mA = Bn = Cp .

8. Поверхности второго порядка

Понятие поверхности.

Поверхностью второго порядка будем называть поверхность, опреде- ляемую в декартовой системе координат уравнением второго порядка

а11х2+2а12ху+2а13хz+2a14x+a22y2+2a23yz+2a24y+a33z2+2a34z+a44=0.

51

Все поверхности второго порядка разделяются на пять классов:

1.Эллипсоиды.

2.Гиперболоиды.

3.Параболоиды.

4.Цилиндры.

5.Конусы.

Следует отметить, что уравнения поверхностей, приведенные далее, записаны в специально выбранных декартовых координатах, которые называются каноническими.

Уравнения некоторых поверхностей.

1. Эллипсоид

Замечание. Если a=b=c=R, то в этом случае эллипсоид называется сферой радиуса R с центром в начале координат.

2. Однополостный гиперболоид

3. Двуполостный гиперболоид

4. Эллиптический параболоид

p+ q = 2z , pq>0.

5.Гиперболический параболоид

52

параболический.

При исследовании поверхностей второго порядка важным является построение некоторых сечений: х=Const, y=Const, z=Const. По виду этих сечений возможно установить свойства указанных поверхностей.

9. Элементарная теория линейных операторов

Линейный оператор и его матрица.

Определение. Если каждому элементу x из линейного простран- ства L ставится в соответствие единственный элемент y из линейного

пространства M, то говорят, что задан оператор, действующий из про- странства L в пространство M. Результат действия оператора A на эле- мент x обозначают y = A(x) .

Если элементы x и y связаны соотношением y = A(x) , то y назы-

вают образом x ; а x – прообразом y .

Определение. Множество элементов пространства L, для которых определено действие оператора A, называют областью определения опе- ратора A и обозначают D(A).

Определение. Множество элементов пространства M, которые яв- ляются образами элементов из области определения D(A) оператора A, называют образом оператора A и обозначают Im(A). Если y = A(x) , то

x D(A), y Im(A) .

53