Математика, теория+расчетные 1 семестр

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Нижегородский Государственный Технический Университет им. Р.Е. Алексеева

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

3х1 + 2 х2 =1 − х3 ,

х1 + 3х2 = 5 − 2х3 ,

+ 2 х3 = 5 .

.pdf

Скачиваний:

Добавлен:

28.03.2015

Размер:

767.71 Кб

Скачать

☆

<<< < Предыдущая 1 23 / 113 4 5 6 7 8 9 10 11 > Следующая >>>

a		a	a	...	a	b
a		a	a	...	a	b
	11	12	13		1n	1
0		a22(1)	a22(1)	... an(12)		b2(1)
	0	0	a(2)	...	a(2)	b(2)	.
			33	...	n3	2
... ...			...	...	...	...
	0	0	a(k −1)	... a(k −1)		b(k −1)
			n3		nn	n

Прямой ход закончен. Заметим, что все элементы на главной диа- гонали отличны от нуля. Получили ступенчатую матрицу.

Найти решение системы уравнений можно обратной подстановкой. Для этого из уравнения, соответствующего последней ненулевой строке ступенчатой матрицы, выражаем xn, подставляем его в предпоследнее

уравнение и выражаем xn−1, и т.д.

Рассмотрим алгоритм применения метода Гаусса на простых при- мерах.

x + y =1,

Пример 1. Решить систему

−x − y = 2.

Преобразуем расширенную матрицу системы:
	1 1		1 C2 +C1	~	1 1	1
	1 1		1 C2 +C1		1 1	1
	−1 −1							.
	−1 −1		2		0 0	3
Отсюда следует, что r( A) =1, r( A\| b) = 2 , т.е. исходная система несо-
вместна.
Пример 2. Решить систему x + y =1,
		−x − y = −1.
Исследуем систему на совместность:
	1 1	1 C2 +C1			1 1		1
	1 1	1 C2 +C1			1 1		1
				~				.
−1 −1		−1			0 0		0

Отсюда следует, что r( A) = r( A | b) =1 – система совместна.

Полученная система содержит одно уравнение с двумя неизвестны- ми. Решение этой системы может быть найдено только в том случае, если мы придадим произвольное действительное значение одному из неиз- вестных. Тогда другое неизвестное можно выразить через первое.

Заметим, что неизвестные, значения которых можно выбирать про- извольно, называют свободными. Число свободных неизвестных опреде- ляется по формуле n − r , где n – число неизвестных в исходной системе,

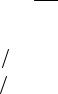
r – ранг матрицы системы (совпадающий с рангом расширенной матри- цы в силу совместности системы).

В данном случае n − r =1. Положим y = C ; тогда x =1 −C . В итоге по- лучаем общее решение системы:

1	−C	, где C	– произвольная постоянная.
x =	C

Придавая постоянной C различные действительные значения, по- лучаем бесконечное множество решений исходной системы.

x − 2 y +3z = 0,

Пример 3. Решить систему

2x + y − z = 0.

Данная система является совместной, т.к. она однородна (все сво- бодные члены равны нулю). Однородная система всегда имеет нулевое

(или тривиальное) решение: x = y = z = 0 .

Преобразуем расширенную матрицу системы:

1	−2 3		0 C2 −2C1	1	−2 3 0
	1	−1		~	.
2			0	0	5 −7 0
Имеем r( A) = r(A \| b) = 2 –		система		совместна. Тогда n − r = 3 − 2 =1 –

количество свободных неизвестных. Полагая z = C (где C – произвольная постоянная), получим

x − 2 y +3C = 0,
	5y −7C = 0.

Отсюда x = −C5 , y = 75C . Таким образом, общее решение системы имеет вид

	−C 5
	7C 5	, где C	– произвольная постоянная.
x =	7C 5	, где C	– произвольная постоянная.
	C
	C

Теорема (о числе решений). Пусть для системы m линейных уравнений с n неизвестными выполнено условие совместности, т.е. ранг r матрицы системы равен рангу ее расширенной матрицы. Тогда, если ранг матрицы системы равен числу неизвестных ( r = n ), то система име- ет единственное решение. Если же ранг матрицы системы меньше числа

неизвестных ( r < n ), то система имеет бесконечное множество решений, а именно: некоторым n − r неизвестным можно придавать произвольные значения, тогда оставшиеся r неизвестных определятся уже единствен- ным образом.

Метод Гаусса-Жордана решения линейных систем Метод Гаусса-Жордана отличается от метода Гаусса тем, что при

выполнении вычислений прямого хода на каждом k-м шаге делим k-е уравнение на a(k−1)kk≠ 0 и исключаем из каждого столбца все элементы кроме ведущего, который равен единице.

Тогда в конце прямого хода имеем

	1	0	0 ...	0	b1(*)

	0	1	0 ..	0	b(*)
					2
... ..			...	..	.
	0	0	0 ...	1
					b(*)
					n

и очевидно, что последний столбец содержит решение системы.

Расчетные задания

Задача 1. Проверить невырожденность системы линейных урав- нений и решить их тремя способами: по формулам Крамера, матричным методом, методом Гаусса.

	2 x1 + 3 x 2 − x 3 = 5 ,			x1 + 3 x 2 − x3 = −1,
1.1.		3 x1 − x 2 + x 3 = 4 ,	1.2.		x1 − x 2 + 5 x3 = 9 ,

		x1 + x 2 + x 3 = 6 .			2 x1 + x 2 − 2 x3 = 3 .

	4 x1 + x2 − x3 = 6 ,			x1 − 2 x2 + x3 = 4 ,
1.3.			1.4.		2 x1 − x2 − 3 x3 = 5, .
	x1 − x2 + 2 x3 = −3,
		2 x1 − 7 x2 + x3 = 0 .
				x1 + 3 x2 − x3 = −1 .
		x1 + x2 − x3 = −2 ,		3 x1 − 3 x 2 + 4 x 3 = 7 , .
1.5.		2 x1 + 4 x2 + 3 x3 = 3,	1.6.		x1 + x 2 − 5 x 3 = − 6 ,

		3 x1 − 2 x2 + 5 x3 = 1 3 .			2 x1 − x 2 + x 3 = 2 .

	x1 + x 2 − x3 = 6 ,
1.7.		2 x1 + 3 x 2 − 4 x3 = 21 ,

		7 x1 − x 2 − 3 x3 = 6 .

	4 x1 + 2 x 2 − x3 = 0 ,
1.9.		x1 + 2 x 2	+ x 3 = 1,

		x 2 − x 3	= −3 .

		2 x1 − x 2 + 5 x3 = 4 ,
1.11.		5 x1 + 2 x 2	+ 1 3 x3 = 2 ,

		3 x1 − x 2 + 5 x3 = 0 .

		x1 + 2 x 2 + 3 x 3 = 1,
1.13.		5 x1 + 8 x 2 − x 3 = 7 ,

		2 x1 − 3 x 2 + 2 x 3 = 9 .

		3 x1 + x 2 + x3 = 8 ,
1.15.		x1 + 2 x 2	− x3 = 2 ,

		2 x1 − 3 x 2 + 2 x3 = 2 .

		x1 + 5 x 2 + x3 = 0 ,
1.17.		2 x1 − 4 x 2	− 3 x3 = −1 ,

		3 x1 + 4 x 2 + 2 x3 = 8 .

	3 x1 + 2 x 2 + 5 x 3 = − 1 0 ,
1.19.		2 x1 + 5 x 2 − 3 x 3 = 6 ,

		x1 + 3 x 2 − 6 x 3 = 1 2 .

		x1 + 2 x2 + x3 = 8 ,
		3 x1 − 2 x 2	− 3 x3 = −5 ,
1.21.
		3 x1 − 4 x 2 + 5 x3 = 1 0 .

4 x

+ 2 x

− x

= 0,

1.8.

+ 2 x2

+ x3

= 1,

x2 − x3 = −3.

x1 + 2 x2 + 3 x3 = 6,

1.10.

2 x1

+ 3 x2

− x3

= 4,

3 x1 + x2 − 4 x3 = 0 .

2 x1 − 3 x2 + 5 x3 = 1 1 .

1.12.

3 x1

− x2

+ 5 x3

= 1 6 ,

x1 + 2 x2 − 4 x3 = −7 .

x2 + 3 x3 = −6 ,

1.14.

− 2 x2 − x3

= 5,

3 x1 + 4 x2 − 2 x3 = 1 3 .

2 x

+ 3 x

− x

= 4,

1.16.

+ 2 x2

+ 2 x3

= 5,

3 x + 4 x

− 5 x

= 2.

2 x1 − x2

= −1,

1.18.

− x3

= −2 ,

x1 − 2 x2

x2 + x3 = −2.

2 x

+ x

− x

= 0,

1.20.

3 x2

+ 4 x3 = −6,

+ x

= 1.

2 x1 − 3 x 2 − x3 = −6 ,

1.22.

3 x1

+ 4 x 2 + 3 x3 = −5 ,

x1 + x 2 . + x3 = −2 .

2 x1 − x 2 = 0 ,

4 x1 − x2 − 3 x3 = 1,

1.23.

+ 2 x 2

− x3

= −2 ,

1.24.

3 x1 + 6 x2

+ 2 x3 = 4,

x 2 . + x3 = −5 .

2 x1 + 4 x2 . + x3 = 4.

+ 4 x

+ 2 x

= 8,

x − x

− 3x

=13,

1.25.

2 x

− 4 x

− 3x

= −1,

1.26.

2x + x

− x

= 0,

x1 + 5x2 . + x3

= 0.

− 2x

= −15.

5x1 + 8x2 − x3 = 7,

2 x 2 − x 3 = 2 ,

1.27.

2 x

− 3x

+ 2 x

= 9,

1.28.

3 x

−

4 x

− 2

x + 2 x

. + 3x

=1.

2 x

= 6

4 x

+ 2 x

−

= 1 2 ,

−x

+ 4 x

+ 2 x

= 12,

1.29.

1.30.

+ 2 x 2

+ x3

= 7 ,

x1 + x2

+ 2 x3

= 7,

x 2 − x3 = −1 .

−x1 + x3 = −1.

Задача 2. Исследовать систему и в случае совместности решить ее.

6 x 1 + 2 x 2 − x 3 = 1 ,

2 x1 + 3 x2 + 4 x3 = 1,

2.1.

x 1 −

2 x 2

2 x 3 = 3 ,

2.2.

x1 − 2 x2

+ x3

= −3,

− 4 x 1 − 6 x 2 + 5 x 3 = 5 .

5 x1 − 3 x2 + 7 x3 = 2 .

4 x 1 − 2 x 2 − x 3 = 1,

x1 − 2 x 2 + x 3 = 6 ,

2.3.

x 1

x 2

+ 3 x 3 = 3 ,

2.4.

2 x1 + x 2 − x 3 = 2 ,

3 x1 + 4 x 2 − 3 x 3 = − 2 .

x 1 − 5 x 2 . − 10 x 3 = 0 .

x 1 + x 2 + 2 x 3 = − 3 ,

x 1 + x 2 − x 3 = 2 ,

2.5.

−

x 1

+ 5 x 2

−

x 3 = 2 ,

2.6.

3 x 1

− 3 x 2

+ 2 x 3 = 5 ,

2 x 1 + 2 x 2 + 4 x 3 = − 6 .

9 x 1 − 3 x 2 + x 3 = 16 .

x 1 − x 2 − 3 x 3 = 2 ,

2 x1 + 3 x2 − 4 x3 = 1,.

2.7.

− 2 x 1

+ x 2

+ 5 x 3 = 3 ,

2.8.

− 5 x1

+ x2

= 1,

− 7 x 1 + 5 x 2 + 19 x 3 = 0 .

− 3 x1 + 4 x2 − 4 x3 = 2 .

		− x 1 + x 2 − 3 x 3 = 1,
2.9.		x 1 + 4 x 3 = 3 ,
		− 3 x 1 + x 2 − 11 x 3 = − 5 .
		− 3 x 1 + x 2 − 11 x 3 = − 5 .
	x1 + 2 x2 + x3 = 1,
2.11.		2 x1 + 5 x2 − x3 = 4,
2.11.		2 x1 + 5 x2 − x3 = 4,
		− x2 + 3 x3 = −2 .
		− x2 + 3 x3 = −2 .
	− x1 + 10 x 2 − 2 x 3 = 7 ,
2.13.		2 x1 + x 2 − 5 x 3 = 3,
2.13.		2 x1 + x 2 − 5 x 3 = 3,

	12 x1 − 15 x 2 − 21 x 3 = 1 .
		2 x1 + 3 x 2 − 4 x 3 = 1,
2.15.		− 5 x1 + x 2 = 1,
2.15.		− 5 x1 + x 2 = 1,
		− 4 x1 + 11 x 2 − 12 х3 = 5 .
		− 4 x1 + 11 x 2 − 12 х3 = 5 .
		3 x1 + 2 x 2 + 4 x 3 = 1,
2.17.		− 2 x1 + x 2 + х3 = − 3 ,
2.17.		− 2 x1 + x 2 + х3 = − 3 ,
		− 3 x1 + 5 x 2 + 7 х3 = 2 .
		− 3 x1 + 5 x 2 + 7 х3 = 2 .
		x1 − 2 x2 + x3 = 6,
2.19.		− x1 + x2 + 2 x3 = 2,
2.19.		− x1 + x2 + 2 x3 = 2,
		− 3 x1 + 4 x2 + 3 x3 = −2.
		− 3 x1 + 4 x2 + 3 x3 = −2.
		x 1 + 2 x 2 + 5 x 3 = 3 ,
2.21.		5 x 1 + x 2 − 7 х 3 = 1 ,
		− 11 x 1 − 4 x 2 + 9 х 3 = −
		− 11 x 1 − 4 x 2 + 9 х 3 = −
		x 1 − x 2 − 3 x 3 = 4 ,
2.23.		2 x 1 − 2 x 2 − 6 х3 = 1 ,
		3 x 1 − 3 x 2 − 9 х3 = − 2 ,
		3 x 1 − 3 x 2 − 9 х3 = − 2 ,

		x 1	+ 3 x 2	= 1 ,
2.10.		2 x 1 + 6 x 2 +		x 3 = 1 ,
2.10.		2 x 1 + 6 x 2 +		x 3 = 1 ,

	x 1 + 5 x 2 − 4 x 3 = 2 .
	x 1 + 5 x 2 − 4 x 3 = − 3 ,
2.12.		x 2	+ 3 x 3	= 2 ,
2.12.		x 2	+ 3 x 3	= 2 ,
		x 1 + 7 x 2 + 2 x 3 = 1 .
		x 1 + 7 x 2 + 2 x 3 = 1 .
		x 1 − x 2 + 3 x 3 = 2 ,
2.14.		− x 1 +	x 2 − 3 x 3 = 0 ,
2.14.		− x 1 +	x 2 − 3 x 3 = 0 ,
		7 x 1 + 5 x 2 = 0 .
		7 x 1 + 5 x 2 = 0 .
		2 x1 + 3 x 2 − x3 = 2 ,
2.16.		− 4 x1 − 5 x 2 + x3 = −3,
2.16.		− 4 x1 − 5 x 2 + x3 = −3,
		− 2 x1 − x 2 − x3 = 0 .
		− 2 x1 − x 2 − x3 = 0 .
		x1 + 6 x 2 + x 3 = 1,
2.18.		3 x1 + x 2 − x 3 = − 2 ,
2.18.		3 x1 + x 2 − x 3 = − 2 ,
		7 x1 + 8 x 2 − x 3 = − 3 .
		7 x1 + 8 x 2 − x 3 = − 3 .
	x 1 − 5 x 2 − 10 x 3 = 0 ,
2.20.		x 1 +	x 2 + 3 х3 = 3 ,
2.20.		x 1 +	x 2 + 3 х3 = 3 ,
		4 x 1 − 2 x 2 − х3 = 1 .
		4 x 1 − 2 x 2 − х3 = 1 .
		x 1 − x 2 + x 3 = 2 ,
2.22.		3 x 1 +	2 x 2	− 3 x 3 =	5 ,
5 .		9 x 1 + x 2 − 3 x 3 = 16 .
5 .		9 x 1 + x 2 − 3 x 3 = 16 .
		x 1 + 2 x 2 − 7 x 3 = − 2 ,
2.24.		− x 1	− 2 x 2	+ 3 х 3 =	4 ,
2.24.		− x 1	− 2 x 2	+ 3 х 3 =	4 ,
		− 2 x 1 − 4 x 2 + 2 х 3 = 10
		− 2 x 1 − 4 x 2 + 2 х 3 = 10

		3 x 1 + 2 x 2 − 3 x 3 = − 1				x 1 + 3 x 2 = 2 ,
2.25.		x 1 +	x 2 + 7 х 3 = 2 ,	2.26.		x 1 + 6 x 2 + x 3 = − 5 ,

		− 8 x 1 − 5 x 2 + 16 х 3 =				2 x 1 + 9 x 2 + x 3 = − 3 .

	3 x1 + 2 x 2 − 4 x 3 = 1,					3 x 1 + x 2 + x 3 = 4 ,
2.27.		x1 − 5 x 2 = 1,		2.28.		2 x 1 − x 2 − 2 x 3 = 1 ,

		4 x1 − 3 x 2 − 4 х3 = 2 .
					x 1 + 2 x 2 + 3 x 3 = 3 .
		7 x 1 + 5 x 2 = 0 ,				x1 + 2 x 2 + 3 x 3 = 1,
2.29.		− x 1 + x 2	− 3 x 3 = 0 ,	2.30.		− 2 x1 − 4 x 2 − x 3 = − 2 ,

		x 1 + x 2 + 3 x 3 = 2 .				− x1 − 2 x 2 + 2 x 3 = − 1 .

Методические указания

Задача 1. Проверить невырожденность системы линейных урав- нений и решить по формулам Крамера.

												−1 2 0
Решение. Запишем матрицу системы											А=		3		1 1 . Проверяем


												−2 −1 0
невырожденность системы. Для этого вычисляем определитель																				матри-
цы А разложением по третьему столбцу:									=	−1		2	0	=1(−1)			−1	2	=−5≠0.


											3	1	1
										−2 −1 0							−2	−1
По правилу Крамера система имеет										−2 −1 0
По правилу Крамера система имеет										единственное решение, которое
находится по формулам:					х1 = 1 ,		х2 =		2 ,		х3	=	3 .		Определители i
получаются из определителя системы									заменой i-го столбца столбцом
свободных членов
	8	2	0			− 1 8 0										− 1		2		8
	8	2	0			− 1 8 0										− 1		2		8
1 =	2	1	1	= 10 ,	2 =	3	2 1	= −15 ,					3 =			3		1		2	= −25 .
	1 − 1 0					− 2 1 0										− 2 − 1 1
							30

Находим решение: х1

=−2,

х2

−15

=3,

х3

−25

=5.

−5

Ответ: х1= –2, х2=3, х3=5.

Задача 2. Исследовать систему и в случае совместности решить ее.

3 x 1 + 2 x 2 − x 3 = 1;

x 1 + 3 x 2 + 2 x 3 = 5 ;

5 x 1 + 8 x 2 + 3 x 3 = 11 ;

x 1 + x 2 = 1 .

Решение. Используя теорему Кронекера-Капелли, проверим со- вместность системы.

Вычисляем методом окаймляющих миноров ранг матрицы системы

	3	2	−1
		3	2
А=	1	3	2
А=		8	3	.
	5	8	3
	1	1	0

Среди миноров 2-го порядка есть отличные от нуля, например

M 2			=	3	2		=	7 ≠	0 .
				1	3
		Все окаймляющие миноры 3-го порядка									3	2	−1		3	2	−1	рав-
											3	2	−1		3	2	−1
											1	3	2	,	1	3	2
											5	8	3		1	1	0
ны нулю. Следовательно, ранг матрицы А: R(											A) = 2 .
		Тем же методом вычисляем ранг расширенной матрицы
				3		2		−	1 1
				1		3		2	5

	А =
	А =			5		8		3	11	.
				5		8		3	11
				1		1		0	1

Получаем, что R( A) = 2 . Поскольку, R( A) = R( A) = k = 2 , то система

совместна. Число неизвестных n = 3 > k, поэтому система имеет бесчис- ленное множество решений.

Находим общее решение системы.

В качестве базисного минора можно взять любой минор порядка

k=2, отличный от нуля, например, М =	3	2	. В этом случае базисными
	1	3

неизвестными окажутся х1 и х2 , а х3 – свободное неизвестное. Решить систему – это значит выразить х1 и х2 через х3.

Записываем укороченную систему, равносильную данной:

где с – любое действительное число.

Полученную систему решаем по правилу Крамера:

=\|М\|=7,	1	=	1 + х3		2	=7х	−7,	2	=	3	1 + х3	= −7х +14.

			5	−2х2	3	3				1	5 −2х3	3

Отсюда	х1 = 1 =х3 −1, х2 = 2 =−х3 +2,		х3 =с R.
			с − 1
Ответ:	общее решение системы		− с + 2	, с R .
Ответ:	общее решение системы	Х =	− с + 2	, с R .
			с
			с

II. Векторы

Теория

1. Операции над векторами

Определение. Вектором AB будем называть направленный отре- зок, имеющий начало в точке А и конец в точке В. Вектор часто обозна-

чают одной буквой, например, a .

Определение. Модулем или длиной вектора а= AB называют

S = a +b + c

Рис. 1

длину отрезка АВ и обозначают символом |

| ≡ |

| ≡ а.

Если

вектор

задан

своими

координатами, то

есть

АB

= (ax , ay , az ) , где ax

= xb

− xa , ay = yb − ya , az = zb

− za ,

(xa , ya , za ),(xb , yb , zb ) –

координаты

точек

В,

то

ax2 + ay2 + az2

или

|АВ|= (xb − xa )2 + ( yb − ya )2 + (zb − za )2 .

Определение. Суммой векторов а, b , с будем называть вектор S , начало которого совпадает с началом первого вектора, а конец совпадает с концом последнего вектора, при условии, что начало последующего вектора совпадает с концом предыдущего (рис. 1).

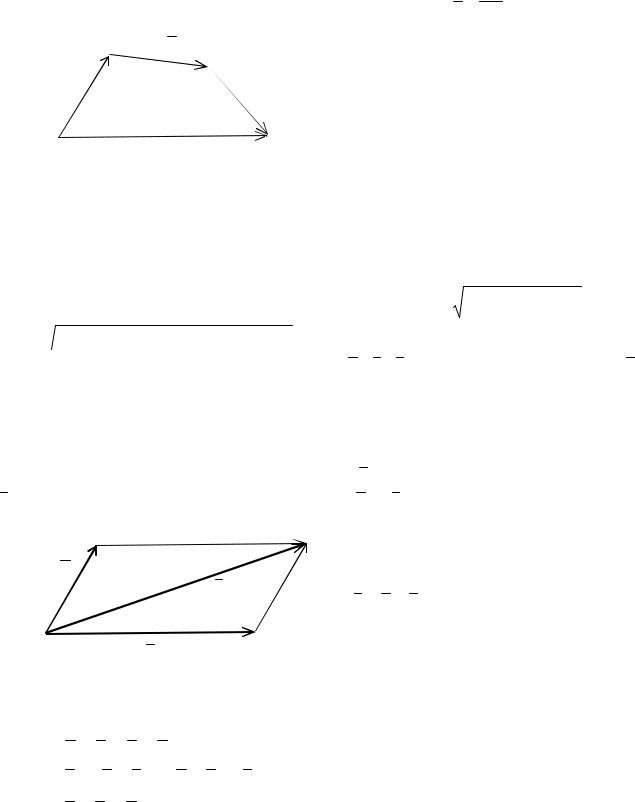
Для сложения двух векторов можно воспользоваться «правилом па- раллелограмма»: суммой двух векторов a и b называется третий вектор c , имеющий общее начало с векторами а и b и совпадающий с диагона-

c = a +b

b Рис. 2

лью параллелограмма, построенного на этих векторах (рис. 2). Операция сложения векторов обладает свойствами:

1)a +b = b + a ;

2)a + (b + c) = (a +b) + c ;

3)a + 0 = a ;

<<< < Предыдущая 1 23 / 113 4 5 6 7 8 9 10 11 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
11.03.201649.15 Кб442Макшеев. Система органов государственной власти в РФ..doc
#
28.03.201561.86 Кб30Маркетинг.docx
#
27.03.2015469.5 Кб34маркитанов кр.doc
#
28.03.20152.57 Mб44Мат. логика.pdf
#
21.04.2019229.24 Кб33матан.docx
#
28.03.2015767.71 Кб41Математика, теория+расчетные 1 семестр.pdf
#
28.03.201516.93 Mб31Математика1.pdf
#
15.08.2019215.2 Кб16матер_лаба1_теория.docx
#
28.03.2015138.99 Кб50Материал для отчета по практике.docx
#
28.03.20154.34 Mб34Материал по экологии.djvu
#
27.03.201598.3 Кб37материаловедение №3 вариант №19 .doc