5.2. Решение задачи нелинейного программирования методом множителей Лагранжа
К нелинейным задачам вида (5.1) применим метод множителей Лагранжа.
Схема решения.
1. Составим функцию Лагранжа:
.
2. Найдем первые частные производные функции Лагранжа:
,
j=1,2,…,n,
,
.
3. Приравняем частные производные к 0; в результате получится система из n+2 уравнений от n+2 переменных:
.
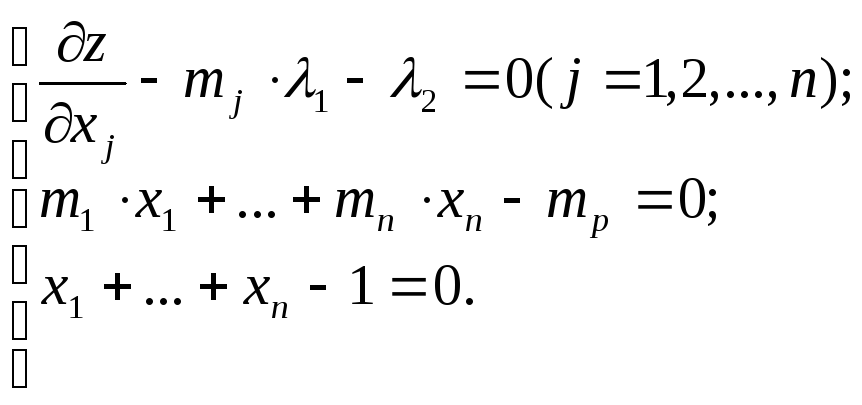4. Найдем решение
системы
.
5. Отбросив две последние переменные, получим условный экстремум функции z.
6. На конкретном примере убедимся в том, что найденные значения доставляют исходной функции минимальное значение. Пример 5.2. решить задачу из примера 5.1 методом множителей Лагранжа.
Составляем функцию Лагранжа:
.
Находим частные производные по каждой из переменных:
;
;
;
;
.
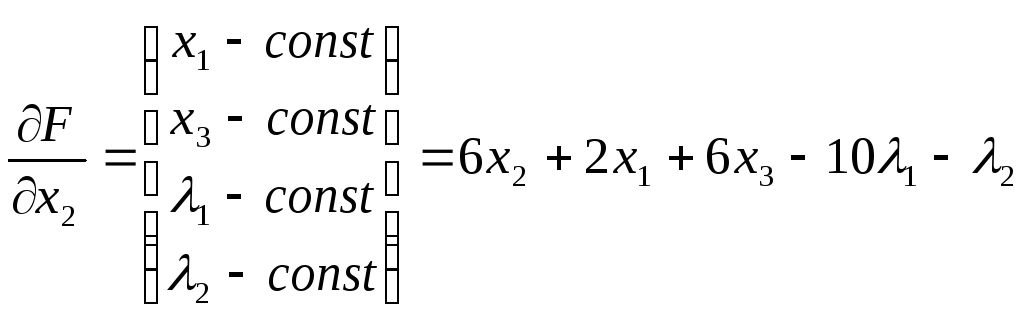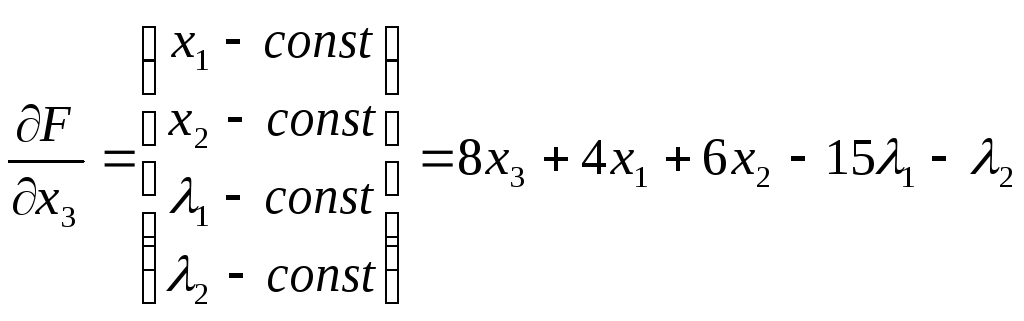Приравниваем их к нулю и получаем систему:
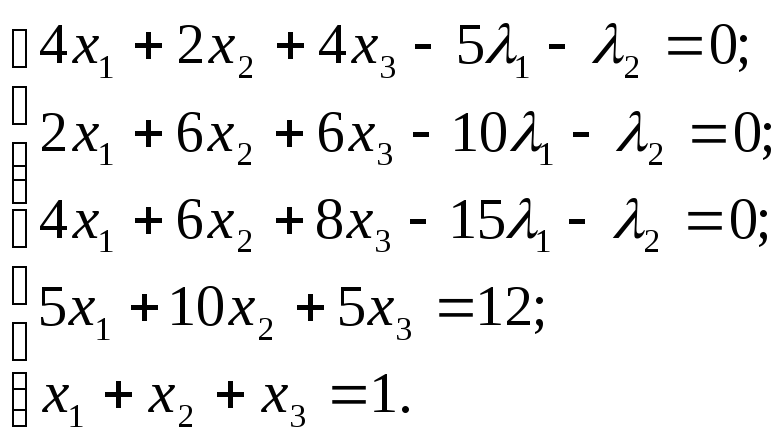
Решаем систему. Получаем:
.
Отсюда, условным экстремумом исходной функции является вектор
,
(5,2)
.
Вектор
также удовлетворяет
системе ограничений исходной задачи.
Но
.
Следовательно, (5,2) – точка минимума.
6. Динамическое программирование
6.1. Принцип оптимальности Беллмана
Этот метод применяется для решения широкого класса задач, в том числе и экономического характера, когда планирование осуществляется в несколько этапов (шагов). Характерной особенностью таких задач является возможность управления рассматриваемым процессом на каждом его этапе. При этом значение целевой функции, которую надо оптимизировать, зависит от последовательности выбираемых на каждом этапе управлений. Динамическое программирование основано на принципе оптимальности Беллмана, согласно которому на любом этапе нужно из нескольких возможных управлений выбирать такое, при котором выигрыш на этом этапе плюс оптимальный суммарный выигрыш на всех последующих этапах был бы максимальным. Этот принцип оптимальности в математической форме можно выразить в виде некоего функционального уравнения, которое необходимо решать на всех этапах, начиная с последнего, причем конкретный вид функционального уравнения Беллмана существенно зависит от специфики рассматриваемой задачи.
6.2. Задача построения оптимального маршрута
Рассмотрим метод динамического программирования на примере задачи построения оптимального маршрута.
Пример. 6.1. Имеется план строительства дороги между пунктами А и В, на котором для любого промежуточного участка дороги известна предполагаемая стоимость его строительства (рисунок 9):
Рис. 9
Требуется построить такой маршрут, соединяющий начальный и конечный пункты, для которого его суммарная стоимость строительства была бы минимальной (маршрут должен проходить только по горизонтальным и вертикальным линиям).
Нарисуем еще раз план строительства, на котором промежуточные пункты изобразим в виде квадратиков (или кружков), куда в процессе решения будут заноситься некоторые числа (рисунок 10):
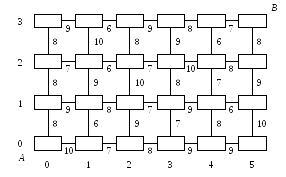
Рис. 10
Пронумеруем
вертикальные линии (i
= 0,1,2,3,4,5) и горизонтальные (j
= 0,1,2,3). Тогда любой промежуточный пункт
будет задаваться парой чисел (i,
j),
что соответствует координатам точки
на плоскости (начальный пункт имеет
координаты А(0,0),
конечный В(5,3)).
Обозначим через
, который идет из пункта (i,
j)
вправо, то есть в пункт (i+1,
j),
а через
- из пункта (i,
j)
в пункт (i,
j+1)
(рисунок 11).
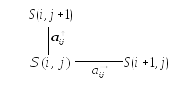
Рис. 11
Пусть S(i, j) – это минимальная суммарная стоимость строительства маршрута, который идет из пункта (i, j) в конечный пункт В(5,3).
Очевидно, что в любом пункте (i, j) выбор одного из двух возможных направлений, вверх или вправо (это есть управления), должен осуществляться исходя из следующего функционального уравнения Беллмана:
.
Схема решения.
1. Очевидно, что
S(5,3)=0.
2. Определим
значения
,
то есть для верхней строки по формуле
,
двигаясь по верхней строке справа налево:
,
,
,
,
.
(в
процессе вычислений эти значения сразу
заносим в соответствующие квадратики).
3. Аналогично
определим значения
,
то есть для крайнего правого столбца
двигаясь сверху вниз, по формуле:
,
,
,
.
4. Далее, определим
все остальные значения S(i,
j)
пользуясь функциональным уравнением
Беллмана, двигаясь справа налево и
сверху вниз:
,
,
,
,
…, и т.д.
.
5. Заносим все вычисления в соответствующие квадратики (рисунок 12);
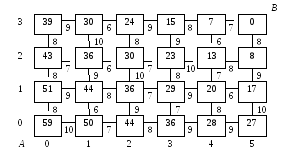
Рис. 12
таким образом,
самый дешевый маршрут имеет стоимость
;
Теперь построим этот оптимальный маршрут, двигаясь уже в направлении от А к В и выбирая в каждом промежуточном пункте то направление (вправо или вверх), которое соответствует минимуму в функциональном уравнении Беллмана (на рисунке этот оптимальный маршрут выделяется пунктирной линией).
Может случится так, что в некоторых промежуточных пунктах придется выбирать минимальное из двух одинаковых чисел. Это означает, что в этом пункте можно выбирать любое из двух направлений, т.е. оптимальных маршрутов может быть несколько.