3.1. Матричная модель игры

При решении экономических задач часто приходится анализировать ситуации, в которых сталкиваются интересы двух или более конкурирующих сторон (конфликтные ситуации). Математической теорией конфликтных ситуаций является теория игр. Теория игр – теория математических моделей, интересы участников которой различны. Задачей теории игр является выработка рекомендаций по рациональному образу действий участников игры (конфликта).

В игре могут сталкиваться интересы двух (парная игра) или нескольких (множественная игра) противников. Существуют также игры с бесконечным числом игроков. Если во множественной игре игроки образуют коалиции, то игра называется коалиционной (в этом случае она сводится к парной).

Одним из основных понятий в теории игр является понятие стратегия – план, по которому игрок совершает выбор в любой возможной комбинации и при любой возможной ситуации. Оптимальной называется стратегия, которая при многократном повторении обеспечивает игроку максимально возможный средний выигрыш.

Рассмотрим парную игру с нулевой суммой. Это означает, что один игрок выигрывает столько, сколько проигрывает его противник.

Пусть игрок А выбирает одну из своих стратегий ,,…,. Его противник, игрокВ, также выбирает одну из своих стратегий ,,…,. Обозначим- выигрыш игрокаА, который получается от применения им стратегии , в то время как игрокВ применил против него стратегию . Тогда все возможные выигрыши можно представить в виде матрицы

.

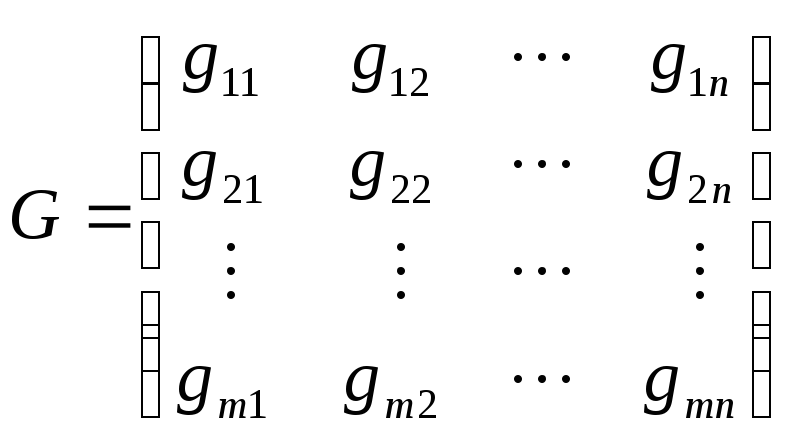Матрица G носит название платежной матрицы или матрицы игры.

Введем два параметра:

(максимальное значение среди всех минимумов , взятых по строкам);

(минимальное значение среди всех максимумов , взятых по столбцам). Параметрыα и β называются соответственно нижней и верхней ценой игры. Очевидно, что выигрыш v игрока А (он также называется ценой игры), то есть выигрыш, получаемый им при применении оптимальной стратегии, находится в пределах:

.

3.2. Игры с седловой точкой

Если

,

То это означает, что в матрице G существует элемент , являющийся одновременно минимумом в строке и максимумом в столбце. Он называется седловой точкой. Игра, удовлетворяющая этому условию, называется вполне определенной или игрой с седловой точкой. Она решается в чистых или первоначальных стратегиях.

Пример 3.1. Пусть матрица игры имеет вид:

.

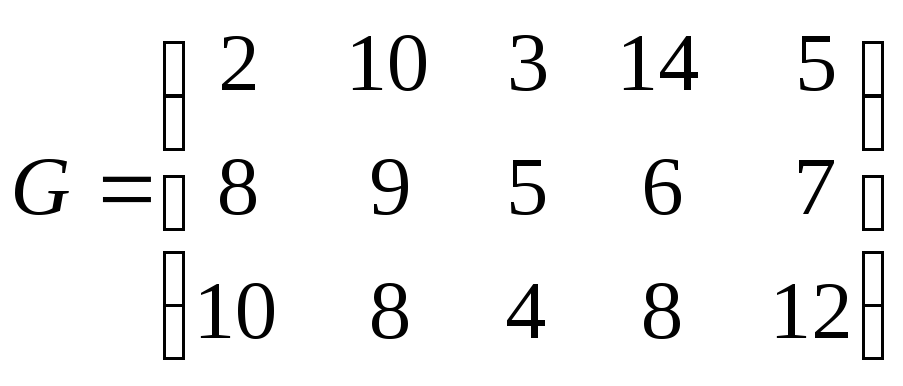Определить, имеет ли игра решение в чистых стратегиях. Если да, то определить оптимальную стратегию игрока А и цену игры.

Определим нижнюю цену игры:

строка 1: ;

строка 2: ;

строка 3: ;

.

Теперь, найдем верхнюю цену игры:

столбец 1: ;

столбец 2: ;

столбец 3: ;

столбец 4: ;

столбец 5: ;

.

Приходим к выводу: данная игра имеет седловую точку (элемент ), задача разрешима в чистых стратегиях. Придерживаясь второй чистой стратегии игрокА обеспечивает себе выигрыш, не меньший 5. Игрок В, придерживаясь своей третьей чистой стратегии, обеспечивает себе проигрыш, не больший 5. Следовательно, цена игры равна 5.

3.3. Игры без седловой точки

Если матрица игры G не имеет седловой точки, то игрок не может придерживаться только одной стратегии. Он случайным образом выбирает стратегии из первоначальных, чистых. Такой выбор называется смешанной стратегией.

Стратегия игрока А задается в этом случае набором вероятностей

.

Можно доказать, что оптимальная смешанная стратегия и выигрыш v игрока А могут быть найдены путем решения ЗЛП:

;

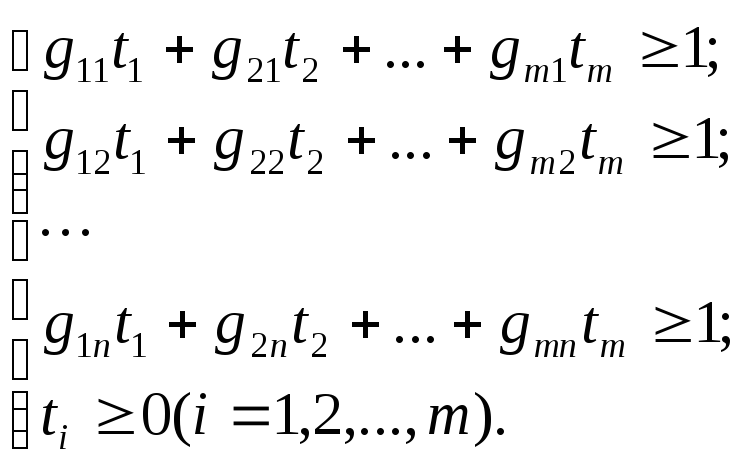
При этом

или . (3.1)

Аналогично, оптимальный набор вероятностей (оптимальная смешанная стратегия)

,

с которыми игрок В применяет свои смешанные стратегии, можно определить, решив следующую ЗЛП:

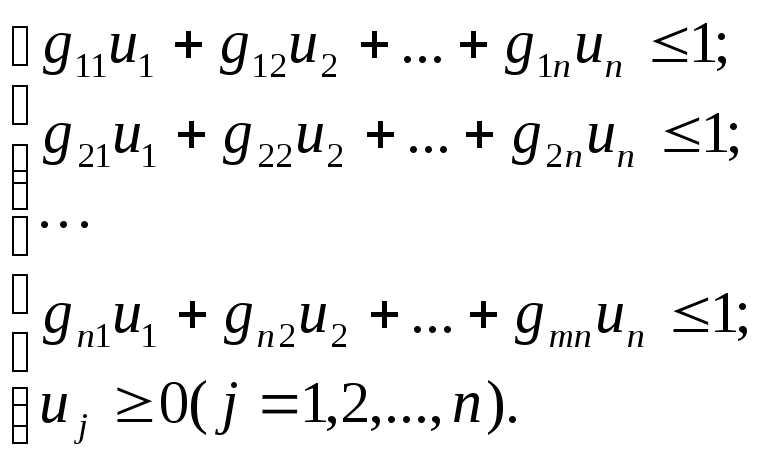; (3.2)

При этом

или . (3.3)

Заметим, что введенные задачи линейного программирования являются парой исходной и двойственной задач. Следовательно, найдя оптимальный план одной из задач, с помощью основных теорем двойственности можно найти оптимальный план другой.

Схема решения.

1. Выяснить, имеет ли данная игра решение в чистых стратегиях.

2. Составить и решить задачу линейного программирования (3,2). 3. Найти цену игры .

4. По формулам (3.3) найти оптимальную смешанную стратегию игрока В. 5. Построить двойственную задачу к (3.2) (см. п. 2.1).

6. С помощью основных теорем двойственности получить оптимальный план построенной задачи.

7. По формулам (3.1) найти оптимальную смешанную стратегию игрока А.

8. Сделать соответствующие выводы.

Пример 2.3. Торговым предприятием разработаны две хозяйственные стратегии ис учетом возможных вариантов поведения покупателей на основе изучения покупательского спроса,и. Платежная матрица представляет собой оценки прибыли (тыс. руб.) торгового предприятия:

.

Необходимо: 1) выяснить, имеет ли игра решение в чистых стратегиях; 2) если игра не имеет решения в чистых стратегиях, то решить ее в чистых стратегиях, используя эквивалентность матричной игры задаче линейного программирования; 3) определить оптимальную смешанную стратегию предприятия.

Найдем верхнюю и нижнюю цену игры:

, ,

;

, ,

.

Так как ,

,

то игра неразрешима в чистых стратегиях.

Составим ЗЛП для нахождения оптимальной стратегии игрока B:

;

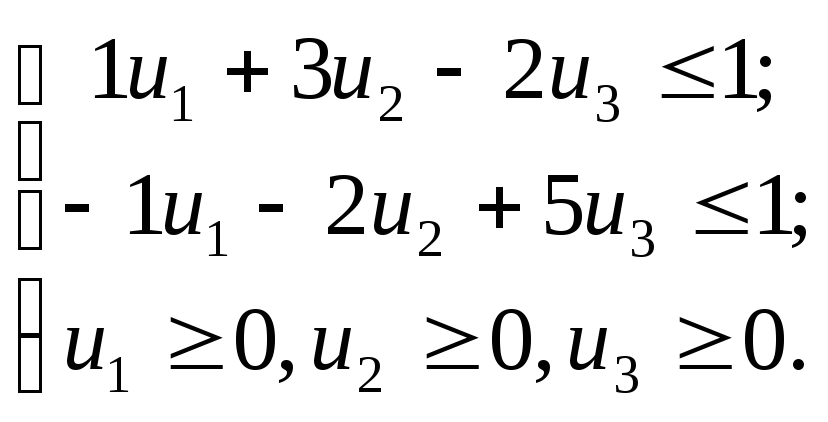
Решаем ее симплекс - методом⁵. Получаем оптимальный план

, .

Находим цену игры:

.

Теперь получаем оптимальную смешанную стратегию игрока В по формуле (3.3):

.

Составляем двойственную задачу:

;

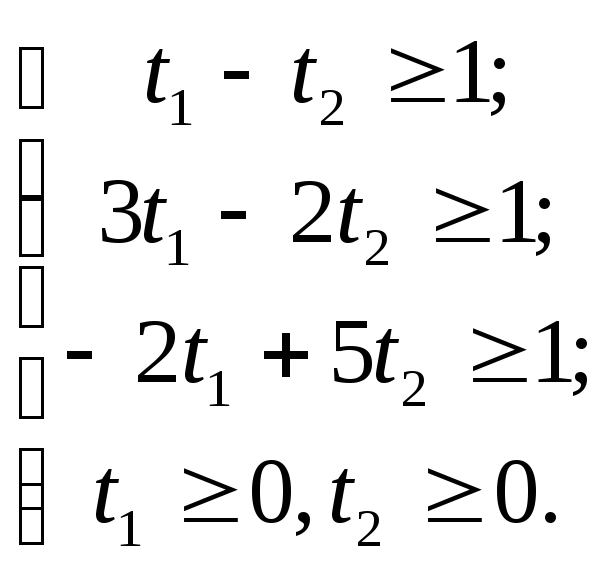
Используя теоремы двойственности, находим оптимальный план этой задачи⁶:

, .

Отсюда, по формулам (3.1) получаем оптимальную смешанную стратегию игрока А:

.

Итак, если предприятие с вероятностью будет придерживаться стратегиии с вероятностью- стратегии, то его прибыль составит(тыс. руб.)