
- •Экономико-математический подход к исследованию финансовых операций
- •Глава I. Основные понятия и формулы
- •1. Задача линейного программирования
- •1.1. Постановка задачи
- •1.2. Графический метод решения
- •1.3. Симплекс – метод решения
- •Алгоритм решения злп симплекс – методом
- •2. Теория двойственности линейного программирования 2.1. Построение двойственной задачи
- •2.2. Получение оптимального плана двойственной задачи
- •2.3. Экономический смысл двойственных оценок
- •3. Элементы теории игр
- •3.1. Матричная модель игры
- •3.2. Игры с седловой точкой
- •3.3. Игры без седловой точки
- •4. Транспортная задача
- •4.1. Постановка транспортной задачи и ее математическая модель
- •4.2. Алгоритм решения транспортной задачи методом потенциалов
- •Алгоритм решения транспортной задачи методом потенциалов
- •5. Задача нелинейного программирования
- •5.1. Задача формирования оптимального портфеля ценных бумаг
- •5.2. Графический метод решения задачи нелинейного программирования
- •5.2. Решение задачи нелинейного программирования методом множителей Лагранжа
- •6. Динамическое программирование
- •6.1. Принцип оптимальности Беллмана
- •6.2. Задача построения оптимального маршрута
- •6.3. Задача распределения ресурсов
- •7. Системы массового обслуживания (смо)
- •7.1. Основные определения
- •7.2. Замкнутые смо с ожиданием
- •7.3. Разомкнутые смо с очередями
- •8. Межотраслевой баланс
- •8.1. Постановка задачи
- •8.2. Модель Леонтьева
- •9. Сетевое планирование
- •II. Типовой расчет
- •Типовой расчет № 4
Глава I. Основные понятия и формулы
1. Задача линейного программирования
1.1. Постановка задачи
Простейшим примером задачи линейного программирования (ЗЛП) является задача оптимального планирования производства.
Предположим, что
предприятие производит два вида изделий
(А
и В),
причем по технологии производства
предусмотрено использование сырья трех
типов. Известно, что для производства
одного изделия А требуется затратить
![]() (ед.) сырья первого типа в количестве,
(ед.) сырья первого типа в количестве,![]() (ед.) – второго типа и
(ед.) – второго типа и![]() (ед.) - третьего типа. Затраты сырья на
производство одного изделияВ
равны соответственно
(ед.) - третьего типа. Затраты сырья на
производство одного изделияВ
равны соответственно
![]() ,
,![]() и
и![]() .
Обеспеченность предприятия сырьем
первого типа составляет
.
Обеспеченность предприятия сырьем
первого типа составляет![]() (ед.), сырьем второго типа -
(ед.), сырьем второго типа -![]() (ед.) и сырьем третьего типа -
(ед.) и сырьем третьего типа -![]() (ед.). Кроме того, известно также, что
прибыль от реализации одного изделияА
равна р
(руб.), а одного изделия В – q
(руб.). Требуется составить такой план
производства изделий из имеющегося в
наличии сырья, при котором суммарная
прибыль от реализации всех изделий была
максимальной.
(ед.). Кроме того, известно также, что
прибыль от реализации одного изделияА
равна р
(руб.), а одного изделия В – q
(руб.). Требуется составить такой план
производства изделий из имеющегося в
наличии сырья, при котором суммарная
прибыль от реализации всех изделий была
максимальной.
Построим
математическую модель задачи. Обозначим
через
![]() - число запланированных к производству
изделийА,
а через
- число запланированных к производству
изделийА,
а через
![]() - число изделий видаВ.
Очевидно, что затраты сырья первого
типа на производство всех изделий
составит величину
- число изделий видаВ.
Очевидно, что затраты сырья первого
типа на производство всех изделий
составит величину
![]() ,
которая не должна превышать запасов
этого сырья
,
которая не должна превышать запасов
этого сырья![]() ,
то есть должно выполнятся неравенство:
,
то есть должно выполнятся неравенство:
![]() .
.
Аналогичные рассуждения для двух других типов сырья дают еще два ограничения:
![]() ,
,
![]() .
.
Кроме того, по
смыслу задачи переменные
![]() и
и![]() не могут быть отрицательными, то есть
не могут быть отрицательными, то есть
![]() ,
,
![]() .
.
Прибыль от реализации всех этих изделий составит величину
![]() .
.
Таким образом, получаем следующую математическую формализацию исходной задачи оптимального планирования:
![]() ;
;
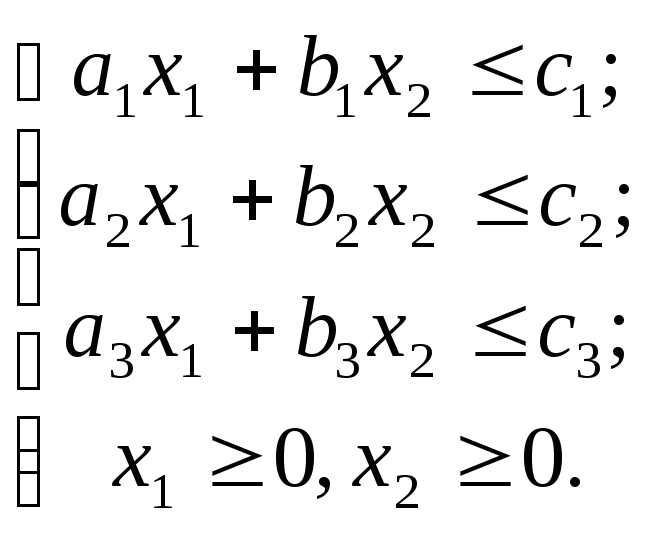
В общем случае ЗЛП формулируется следующим образом:
![]() (или
(или
![]() );
(1.1)
);
(1.1)
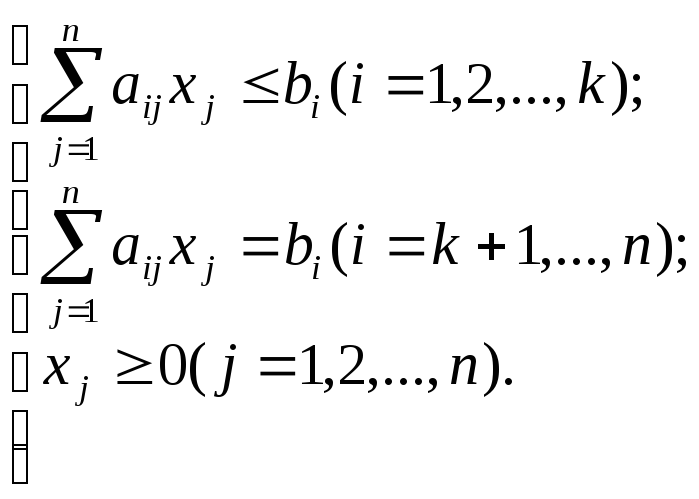 (1.2)
(1.2)
Требуется найти
максимальное (или минимальное) значение
целевой функции z
при условии, что переменные
![]() ,
,![]() ,…,
,…,![]() удовлетворяют заданной системе
ограничений (1.2), среди которых могут
как равенства, так и неравенства.
удовлетворяют заданной системе
ограничений (1.2), среди которых могут
как равенства, так и неравенства.
Термин «задача линейного программирования» объясняется тем, что в постановке этой задаче все функции являются линейными. Функция (1.1) называется целевой функцией или функцией цели. Решением ЗЛП или оптимальным планом задачи линейного программирования называется набор
![]() ,
,
удовлетворяющий системе (1.2) и доставляющий линейной функции оптимальное (максимальное или минимальное) значение.
1.2. Графический метод решения
Этот метод применяется только в том случае, когда число переменных в ЗЛП невелико, то есть n = 2 или, в крайнем случае, n = 3. Рассмотрим этот метод на примере следующей ЗЛП.
Пример 1.1. Предприятие для производства двух изделий (А и В) использует сырье трех типов. Известно, что для производства одного изделия А требуется сырье первого типа в количестве 1 (ед.), второго типа - 3 (ед.) и третьего типа - 1 (ед.), а для производства изделия В - 1, 1 и 2 соответственно. Запасы сырья на предприятии ограничены и составляют величины 6, 12 и 10 соответственно. Известно также, что прибыль от реализации одного изделия А составляет 2 (руб.), а одного изделия В – 3 (руб.). Требуется составить такой план производства изделий из имеющегося сырья, чтобы суммарная прибыль от реализации всех изделий была максимальной.
Составим математическую модель задачи:
![]() ;
;
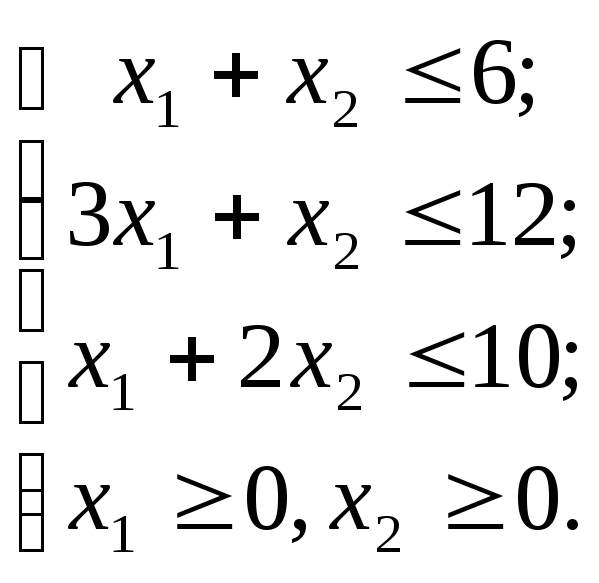 (1.3)
(1.3)
Схема решения.
1. Построим на
плоскости
![]() пять прямых, соответствующих данным
ограничениям:
пять прямых, соответствующих данным
ограничениям:
![]() ;
;
![]() ;
;![]() .
.
Прямые
![]() ,
,![]() и
и![]() надо строить по двум точкам, причем
очень аккуратно и, желательно, на листе
клетчатой бумаге. Прямые
надо строить по двум точкам, причем
очень аккуратно и, желательно, на листе
клетчатой бумаге. Прямые
![]() и
и
![]()
соответствуют координатным осям. Очевидно, что данная система неравенств определяет на плоскости многоугольник допустимых решений (в данном случае многоугольник ABCD, см. рисунок 1).

Рис. 1
2. Найдем координаты всех вершин этого пятиугольника, составив соответствующие системы линейных уравнений и решив их (методом Гаусса или по формулам Крамера):
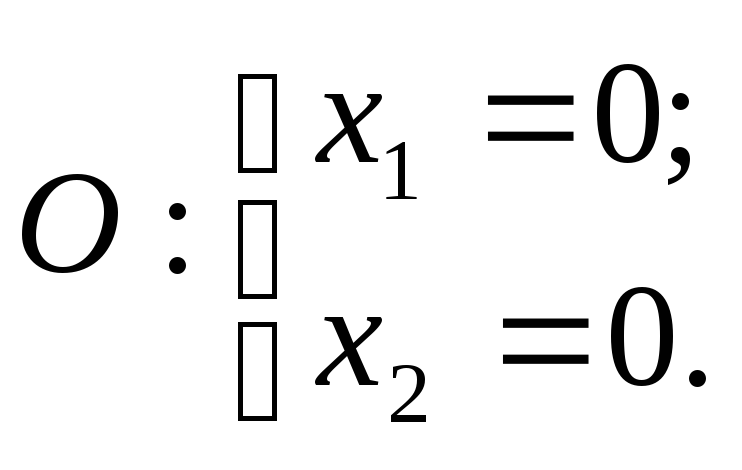 ;
;
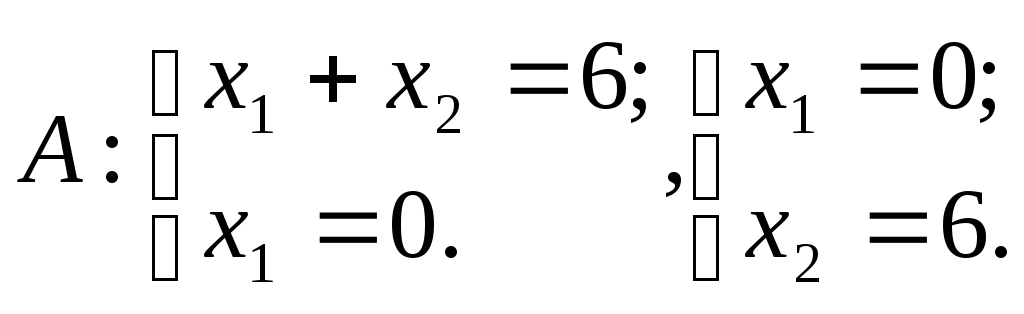 ;
;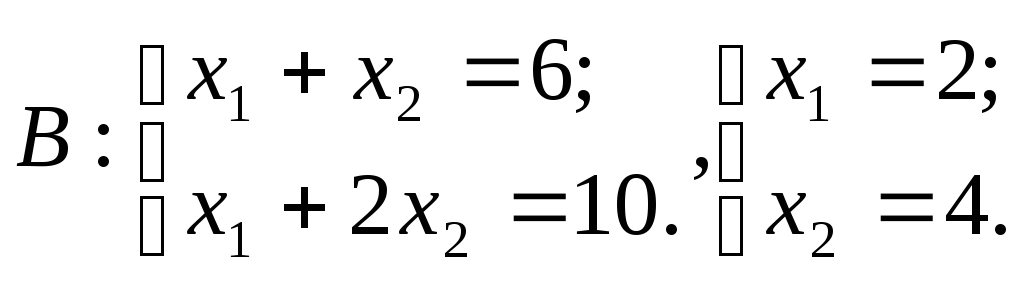 ;
;
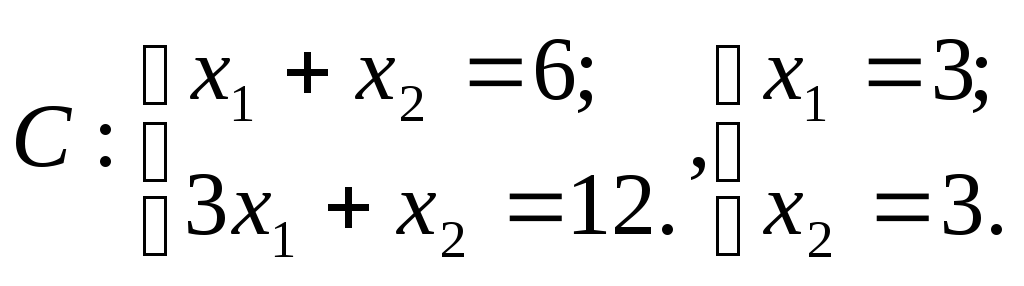 ;
;
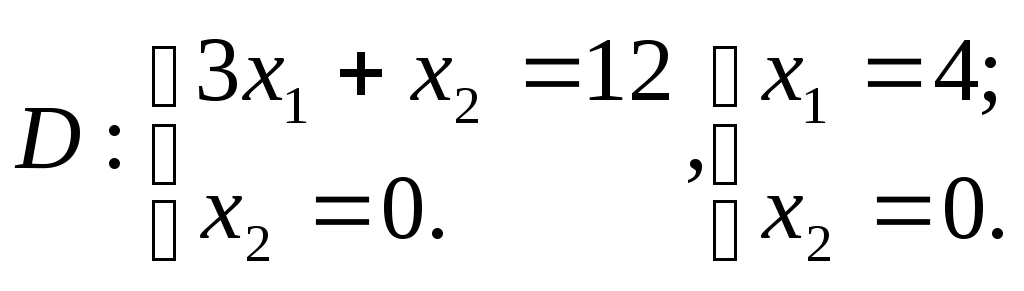
В результате получим следующие точки:
O(0,0), A(0,5), B(2,4), C(3,3), D(4,0).
3. Отметим еще
раз эти точки на плоскости
![]() (рисунок 2), а также построим вектор
(рисунок 2), а также построим вектор![]() ,
координатами которого являются
коэффициенты при неизвестных в целевой
функцииz
(начало вектора
,
координатами которого являются
коэффициенты при неизвестных в целевой
функцииz
(начало вектора
![]() можно взять в любой точке).
можно взять в любой точке).
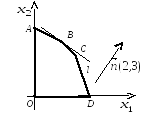
Рис. 2
Очевидно, что
целевая функция
![]() при всевозможных значенияхz
определяет
на плоскости свойство параллельных
прямых, перпендикулярных вектору
при всевозможных значенияхz
определяет
на плоскости свойство параллельных
прямых, перпендикулярных вектору
![]() ,
поэтому максимальное значениеz
на множестве допустимых решений (то
есть оптимальное решение) соответствует
такой прямой из этого семейства, которая
во – первых, как можно дальше расположена
от начала координат, а, во – вторых,
имеет хотя – бы одну общую точку с
многоугольником допустимых решений
(эта прямая l
называется опорной).
,
поэтому максимальное значениеz
на множестве допустимых решений (то
есть оптимальное решение) соответствует
такой прямой из этого семейства, которая
во – первых, как можно дальше расположена
от начала координат, а, во – вторых,
имеет хотя – бы одну общую точку с
многоугольником допустимых решений
(эта прямая l
называется опорной).
4. Построим опорную прямую l. В данном случае она проходит через вершину В(2,4), поэтому координаты этой точки дают оптимальное решение исходной ЗЛП.
Таким образом,
![]() ,
,
![]() ,
,![]() .
.
Итак, для получения оптимальной прибыли в размере 16 (руб.) необходимо выпустить 2 (ед.) продукции А и 4 (ед.) продукции В.
