1.3. Симплекс – метод решения

В п. 1.2 был рассмотрен графический метод решения ЗЛП. В общем случае, каждое ограничение из (1.2) есть уравнение гиперпространства n – мерного пространства с граничной гиперплоскостью

.

Гиперплоскость, ввиду совместности системы образует общую часть, которая называется многогранником решений. Координаты угловых точек многогранника есть опорные планы ЗЛП. Оптимальные планы определяются из опорных.

При n>3 получить оптимальный план графическим или перебором опорных становится практически неразрешимой задачей.

Симплекс – метод ¹ представляет собой итеративную (пошаговую) процедуру, позволяющую за конечное число шагов (их максимальное число равно n-m+1, m – число ограничений в системе (1.2)), последовательно улучшая опорные планы, либо аналитически оптимальный план ЗЛП, либо убедиться, что задача оптимальным планом не обладает.

Основная идея симплекс – метода состоит в следующем. Каждый опорный план определяется базисом из m линейно – независимых векторов. Если план не оптимален, то необходимо выбрать другой базис. Для этого, из старого базиса исключается один из базисных векторов и на его место включается один из бывших небазисных. Тем самым, производится переход от одного базиса к другому, и, следовательно, от одного опорного плана к другому.

Симплекс – методом можно решать только те задачи, у которых:

• система ограничений (1.2) содержит только равенства;

• число уравнений в (1.2) не больше числа переменных в целевой функции (1.1), ;

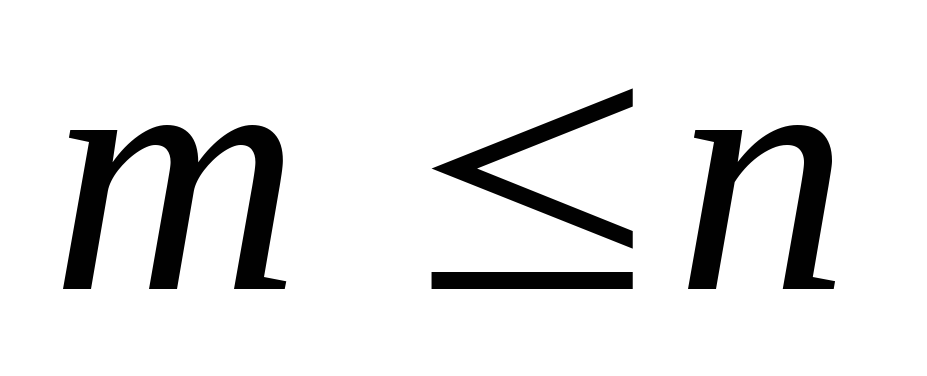• столбец свободных членов (1.2) не содержит отрицательных чисел, .

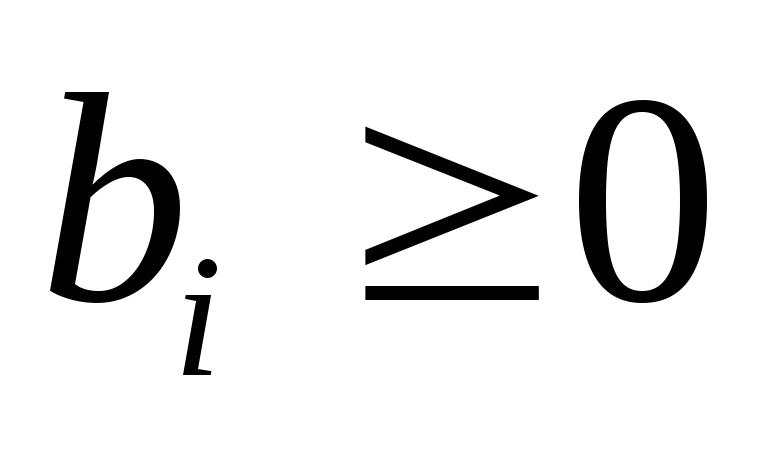Алгоритм симплекс - метода рассмотрим на задаче из примера 1.1.

Пример 1.1. Решить ЗЛП из примера 1.1 симплекс – методом.

Алгоритм решения злп симплекс – методом

Шаг 1. Определение возможности решения ЗЛП симплекс – методом.

Для того, чтобы ЗЛП решить симплекс – методом, необходимо в системе (1.3) от неравенств перейти к равенствам. Для этого, вводим фиктивные переменные ,,. Получаем расширенную ЗЛП:

;

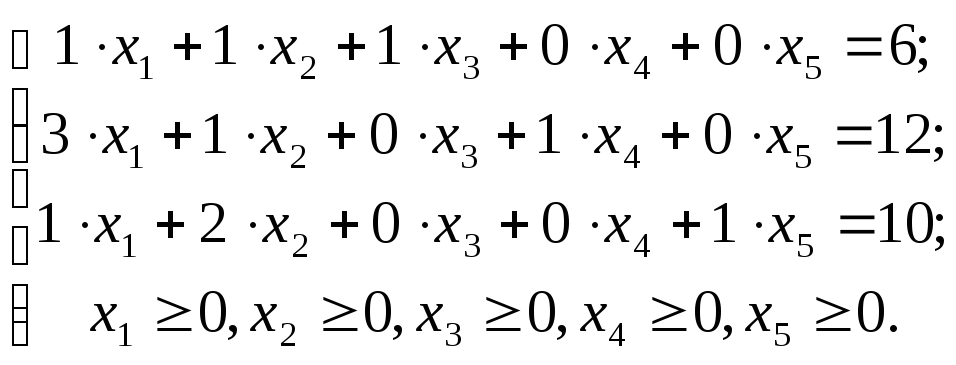
Эта задача может быть решена симплекс – методом, так в ней число переменных 5 больше числа ограничений 3 и столбец свободных членов содержит только положительные числа.

Шаг 2. Получение канонической формы записи ЗЛП.

В нашем случае каноническая форма записи ЗЛП имеет вид:

;

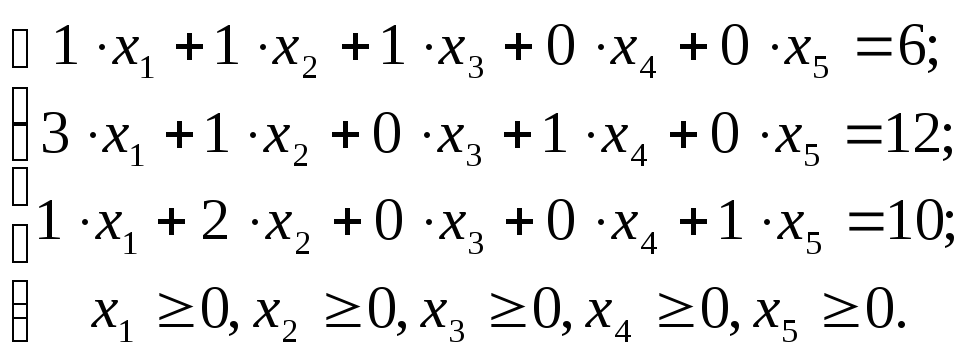(1.4)

Шаг 3. Определение базиса.

Определим векторы -, координаты которых соответствуют столбцу коэффициентов при неизвестных в системе (1.4):

, ,,,.

Система (1.4) содержит m=3 ограничения, поэтому среди векторов

- необходимо в качестве базисных выбрать три вектора. Поскольку векторы,и- единичные, то они очевидно образуют базис (именно в такой последовательности!) трехмерного пространства.

Переменные , номера которых соответствуют базисным векторам, назовем базисными, а остальные приравняем к нулю,

, ,- базисные переменные,

. (1.5)

Коэффициенты линейной функции, номера которых совпадают с номерами базисных векторов, также назовем базисными. Будем представлять их в виде набора, обозначаемого . В нашем случае

.

Шаг 4. Определение начального опорного плана.

Подставим (1.5) в (1.4) и решим систему:

,,,

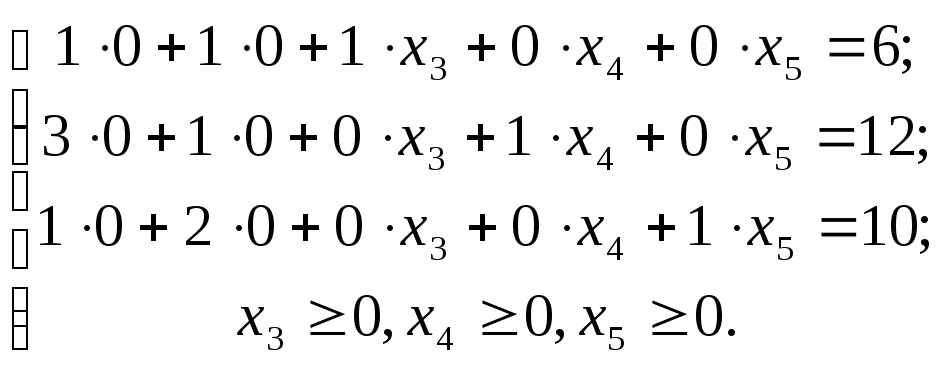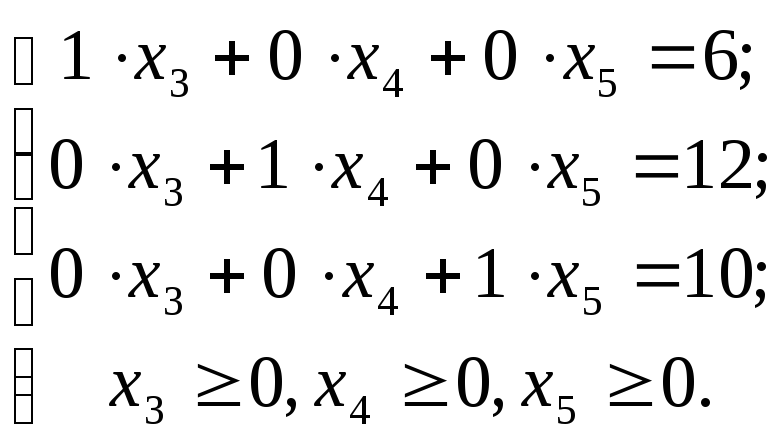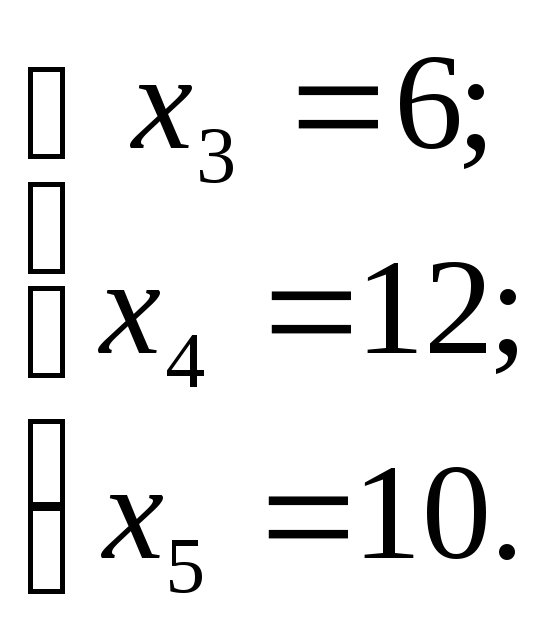, ,. (1.6)

Значения (1.6) запишем в виде вектора

.

Собирая вместе (1.5) и (1.6), получаем начальный опорный план

.

Значение целевой функции для этого плана равно

.

Шаг 5. Проверка оптимальности плана.

Для каждого из векторов определим величину оценки

.

Имеет место утверждение: план ЗЛП, сформулированной на нахождение максимального значения целевой функции, является оптимальным, если

для всех . (1.7)

Заметим, что для базисных векторов обязательно

.

Это свойство удобно применять для проверки правильности произведенных вычислений.

В рассматриваемом примере имеем:

,

,

,

,

.

Получаем: условие оптимальности (1.7) нарушается для векторов и.

Шаг 6. Составление симплекс – таблицы.

Все произведенные расчеты заносим в симплекс – таблицу (таблица 1.1):

Таблица 1.1.

i	Базис
1		0	6	1	1	1	0	0
2		0	12	3	1	0	1	0
3		0	10	1	2	0	0	0
4			0	2	3	0	0	0

Порядок заполнения этой таблицы следующий:

- в первые три строки и последние шесть столбцов поставим коэффициенты из системы ограничений канонической формы ЗЛП;

- последние три вектора {,,} образуют стандартный базис трехмерного пространства, - их номера занесем в столбец «Базис»;

- в верхней строке над всеми векторами {,,,,} поставим соответствующие коэффициенты целевой функции ;

- в столбец «» поставим коэффициенты, соответствующие базисным векторам;

- в четвертой строке в столбце поставим значение целевой функции для начального опорного плана;

- в оставшиеся пять клеток четвертой строки поставим так называемые оценки .

Шаг 7. Переход к новому базису.

Поскольку план не оптимален, то для получения нового опорного плана необходимо построить новый базис. «Претендентами» на включение в базис будут векторы, для которых нарушается условие оптимальности (1.7). Итак, критериями перехода от одного базиса к другому, являются оценки:

, ,,

.

В примере условия оптимальности нарушаются для векторов () и(). Производим требуемые расчеты:

j=1, ;

j=2, ;

.

Последняя оценка показывает, что из базиса исключается вектор и на его место включается вектор. Получили новый базис:

, , ,

.

Элемент , стоящий на пересечении строки и столбца называется разрешающим и помещается в симплекс – таблице в квадратик.

Шаг 8. Определение координат небазисных векторов и оценок оптимальности.

Итак, вектор в новом базисе занимает место вектора . Значит, его новые координаты должны быть равны (0,0,1) (вектор третий в базисе!), а оценка должна быть равна 0. Это означает, что второй столбец симплекс – таблицы из

становится .

(в первых трех строчках матрицы – столбца указаны координаты вектора, а во второй – его оценки). Этот переход можно осуществить с помощью элементарных преобразований:

- из 1 – й строки вычесть 3 – ю строку, умноженную на;

- из 2 – й строки вычесть 3 – ю строку, умноженную на ;

- из 4 – й строки вычесть 3 – ю строку, умноженную на ;

- умножить третью строку на .

А именно

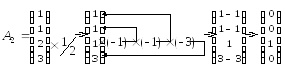
Те же преобразования осуществляем для остальных небазисных векторов:

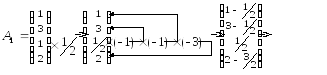
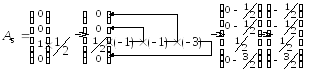
Шаг 9. Получение нового опорного плана.

Получим новый опорный план. Для этого, вектор из таблицы 1.1 подвергнем тем же преобразованиям, что и векторы из предыдущего шага алгоритма:

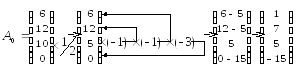
Итак, получен новый опорный план

,

.

Шаг 10. Составление симплекс – таблицы.

Все произведенные в шагах 8 и 9 помещаем в симплекс – таблицу (таблица 1.2):

Таблица 1.2.

i	Базис
1		0	1		0	1	0
2		0	7		0	0	1
3		-3	5		1	0	0
4			-15		0	0	0

Шаг 11. Проверка правильности вычислений.

Чтобы убедиться в правильности всех коэффициентов таблицы, можно сделать контроль вычислений по формулам, которые использовались при заполнении 4 – й строки первой симплекс – таблицы:

;

,

,

,

,

.

Так как все эти числа в точности совпадают с числами 4 – й строки симплекс – таблицы, то это означает, что ошибок в вычислениях нет.

Шаг 12. Проверка оптимальности плана.

Просматриваем последнюю строку симплекс – таблицы. Видим, что условие оптимальности (1.7) нарушено. Следовательно, план не оптимален, условие оптимальности нарушается для вектора .

Далее шаги 7 – 12 повторятся до тех пор, пока не будет выполняться условие оптимальности (1.7), тем самым будет получен оптимальный опорный план.

Шаг 7’.

Так как условие оптимальности нарушается только для одного вектора , то именно он включается в базис. Чтобы определить вектор, исключаемый из базиса, найдем

.

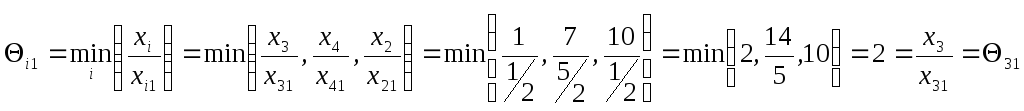Значит, разрешающим элементом является число ( в клетке ). Вектор исключается из базиса и на его место включается вектор . Новый базис:

, , ,

.

Шаг 8’. Из базиса надо убрать вектор , заменив его на . Для этого из столбца

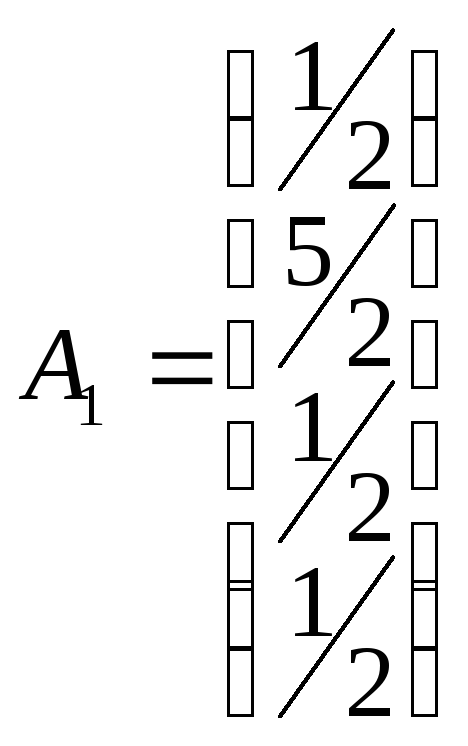надо сделать столбец

при помощи следующих элементарных преобразований:

2 стр. – 1 стр.×5, 3 стр.- 1 стр., 4 стр.- 1 стр., 1 стр.×2. (1.8)

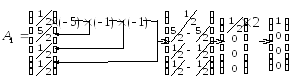
Для остальных векторов получаем согласно (1.8)²:

, .

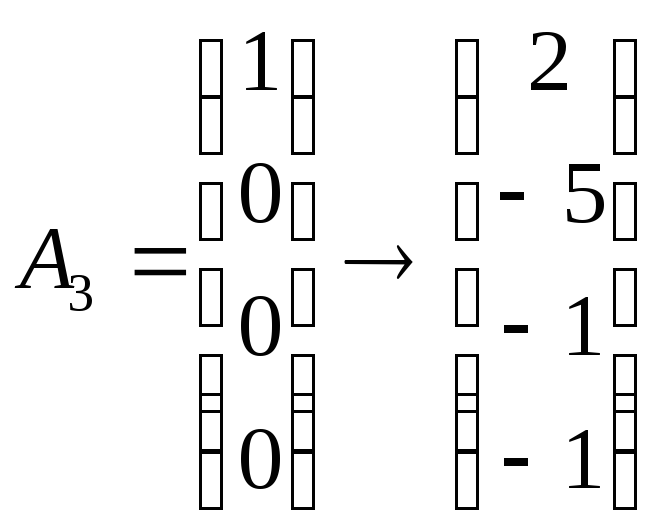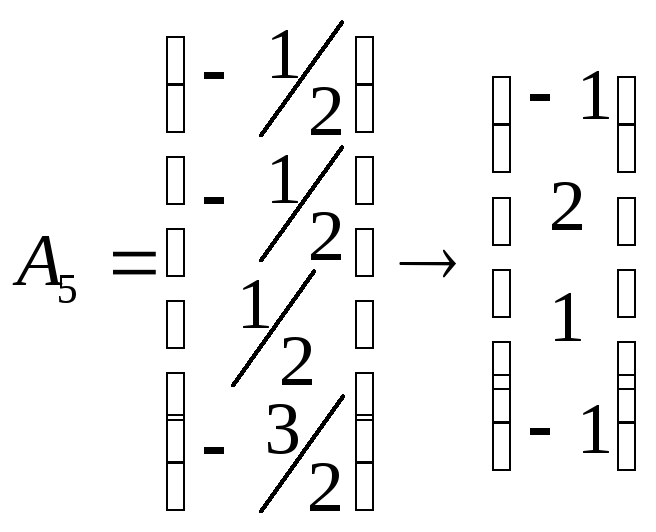Шаг 9’.

Преобразования (1.8) осуществляем над вектором ³:

.

Тем самым, получен третий опорный план

,

.

Шаг 10’.

В результате получим третью симплекс – таблицу:

Таблица 1.3.

i	Базис
1		-2	2	1	0	2	0	-1
2		0	2	0	0	-5	1	2
3		-3	4	0	1	-1	0	1
4			-16	0	0	-1	0	-1

Шаг 11’.

Контроль вычислений показывает⁴, что ошибок нет.

Шаг 12’.

Поскольку все оценки , то этот опорный план является уже оптимальным планом расширенной задачи.

Чтобы перейти к оптимальному плану исходной задачи, необходимо в оптимальном плане расширенной задачи избавиться от фиктивных переменных.

Таким образом, план

является оптимальным планом исходной задачи и доставляет целевой функции максимальное значение

.

Нетрудно заметить, что начальному опорному плану соответствует точкаО на рисунке 1, плану - точкаА, а плану - точкаВ. Заметим также, что максимальное число опорных планов в рассмотренной задаче может быть равным 5-3+1=3.