2. Теория двойственности линейного программирования 2.1. Построение двойственной задачи

С каждой задачей линейного программирования тесно связана другая ЗЛП, которая называется двойственной. Первоначальная задача называется исходной.

Связь исходной и двойственной задач:

1. коэффициенты целевой функции двойственной задачи есть столбец свободных членов системы ограничений исходной;

2. столбец свободных членов системы ограничений двойственной задачи есть коэффициенты целевой функции исходной;

3. матрица системы ограничений (то есть матрица, составленная из коэффициентов при неизвестных) двойственной задачи есть транспонированная матрица системы ограничений исходной (матрицаназывается транспонированной к, если в исходной матрице поменять местами соответствующие строки и столбцы).

Итак, если исходной считать задачу планирования производства (см. п. 1.1),

;

,

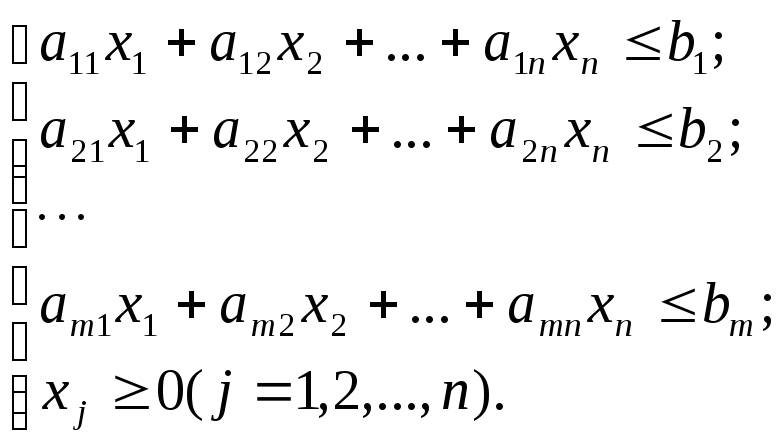то двойственная задача имеет вид:

;

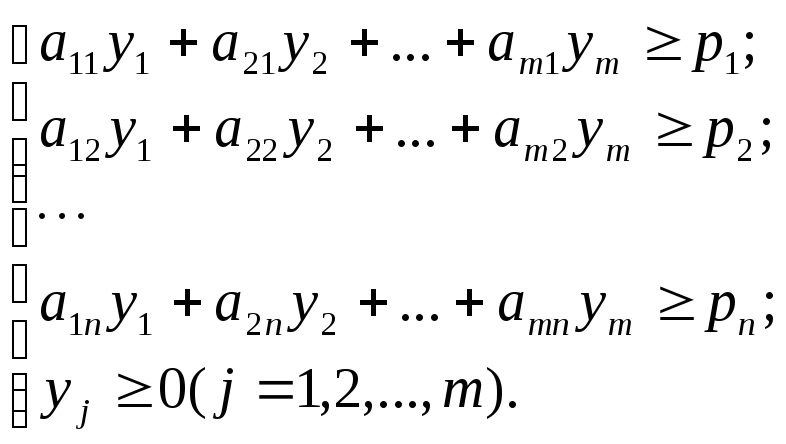
Пример 2.1. Построить двойственную ЗЛП к задаче из примера 1.1.

Используем связь исходной и двойственной задач. Получаем: двойственная ЗЛП к задаче из примера 1.1 имеет вид

;

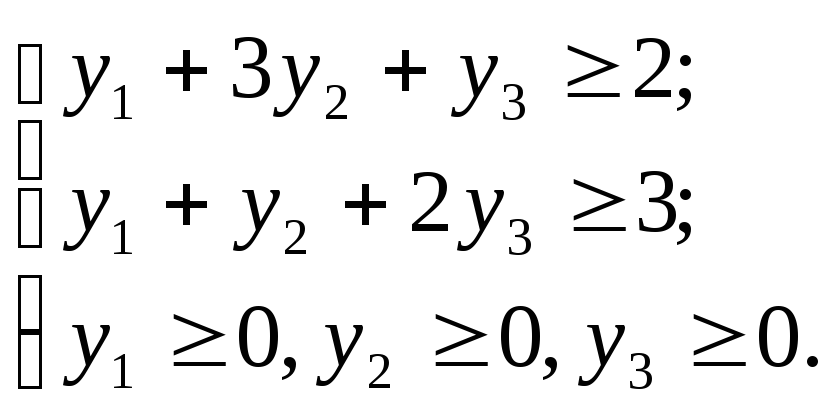(2.1)

2.2. Получение оптимального плана двойственной задачи

Оптимальный план двойственной задачи можно получить любым вышеизложенным способом. Но, наиболее быстрый его поиск производится с помощью основных теорем двойственности.

Теорема 1. Если разрешима одна из двойственных задач, то разрешима и другая, причем значения их целевых функций после подстановки в них компонент оптимального плана равны между собой.

Теорема 2. Если при подстановке компонент оптимального плана исходной задачи в систему ограничений, ограничение номер i выполняется как строгое неравенство, то компонента с тем же номером i оптимального плана двойственной задачи равна 0.

Теорема 3. Если компонента с номером i оптимального плана исходной задачи положительна, то ограничение с тем же номером i двойственной задачи выполняется как строгое равенство.

Пример 2.2. Получить оптимальный план двойственной задачи для задачи из примера 1.1.

Двойственная задача к ЗЛП из примера 1.1. была получена в примере 2.1. Оптимальный план согласно примерам 1.1 и 1.2

, .

Подставим его компоненты в систему ограничений (1.3):

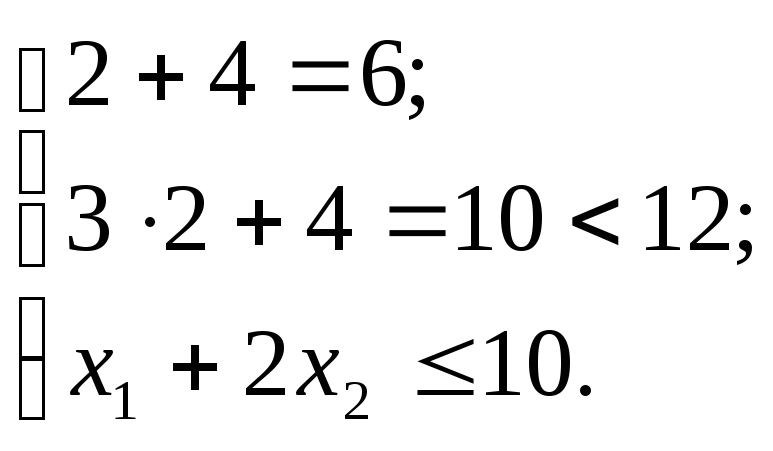
Так как ограничение номер 2 выполняется как строгое неравенство, то согласно теореме 2 двойственности в оптимальном плане двойственной задачи

.

Далее, первая и вторая компоненты оптимального плана исходной задачи положительны, ,, то по теореме 3 двойственности первое и второе ограничение (2.1) выполняются как строгие равенства:

, .

Три полученных равенства образуют систему:

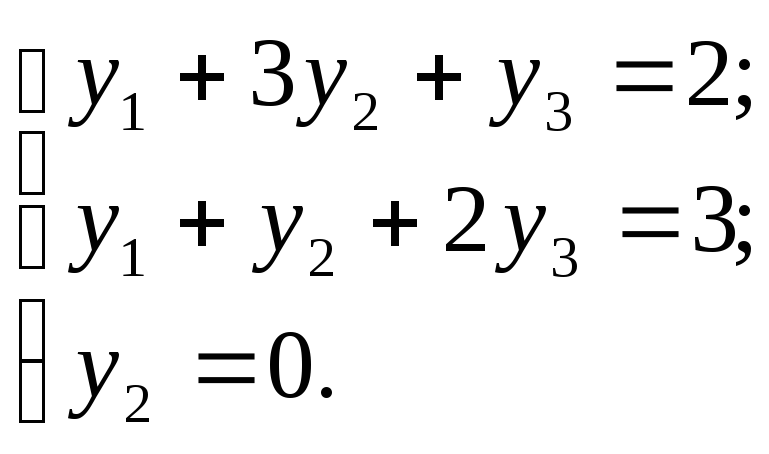
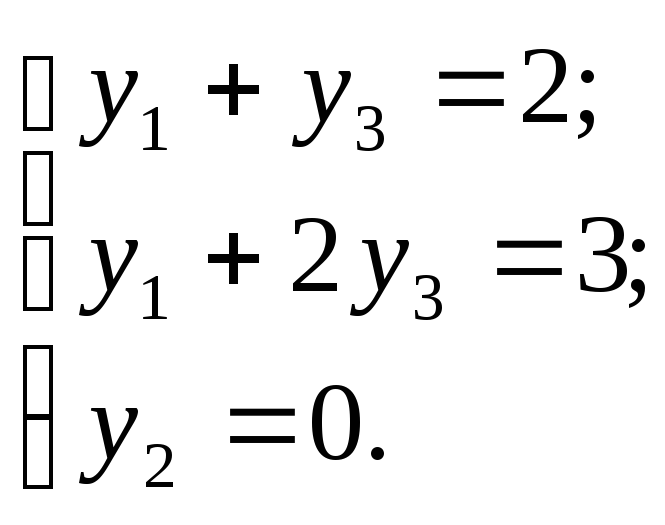
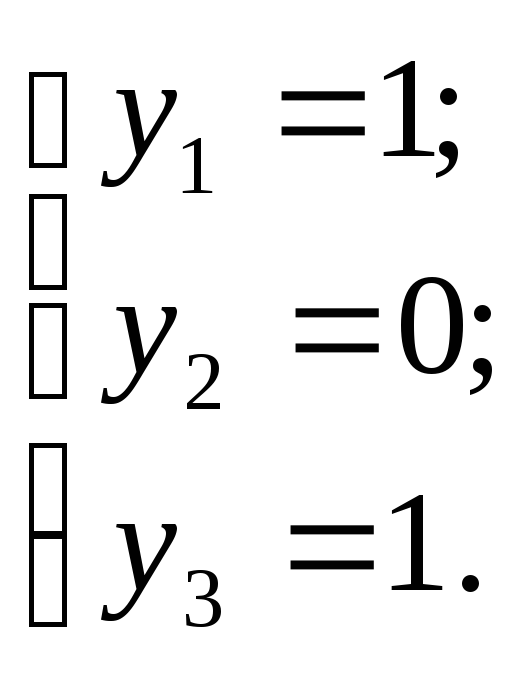
Итак, нами получен план двойственной задачи:

. (2.2)

Поскольку

,

то план (2.2) является оптимальным по теореме 1 двойственности.

2.3. Экономический смысл двойственных оценок

Экономический смысл двойственных оценок раскрывается в основных свойствах двойственности.

Свойство 1. Двойственные оценки показывают, насколько возросло бы значение целевой функции, если величину соответствующего ресурса увеличить на 1 ед.

Свойство 2. Двойственные оценки отражают сравнительную дефицитность ресурсов: чем больше двойственная оценка, тем дефицитнее соответствующий ей ресурс.

Свойство 3. С помощью двойственных оценок можно определить нормы заменяемости ресурсов; имеется в виду заменяемость с точки зрения принятого в задаче показателя эффективности.

Пример 2.3. Произвести экономический анализ оптимального плана (2.1) задачи из примера 2.1.

Пример 2.3. Дать анализ двойственных оценок из примера 2.2.

Анализируем полученный в примере 2.2. оптимальный план (2.2).

Если увеличить первый ресурс на 1 (ед.), то суммарная прибыль увеличится на 1 (руб.). Такой же вывод делаем относительно ресурса третьего типа. Увеличение количества ресурса второго типа не влияет на рост прибыли (так как ).

Максимальные оценки в плане (2.2) соответствуют ресурсам первого и третьего типов. Следовательно, они являются дефицитными. Ресурс второго типа менее дефицитен, так как соответствующая ему компонента минимальная в плане.

Найдем нормы заменяемости ресурсов первого и третьего типов:

.

Это означает что потеря 1 (ед.) ресурса первого типа может быть скомпенсирована 1 (ед.) ресурса третьего типа. При сохранении этой пропорции суммарная прибыль останется на прежнем уровне.