
- •Речевая система
- •Система управления с обратной связью
- •Вернемся к выражению (11) для решения системы (10). Если в этом выражении иизвестны, то можно найтидля всех моментов.
- •Пусть в системе, представленной линейной моделью в пространстве состояний
- •Устойчивость систем
- •Устойчивость линейных непрерывных систем
- •Устойчивость линейных дискретных систем.
- •Критерии устойчивости полиномов
- •Графические критерии устойчивости полиномов Пусть задан полином
- •Алгоритм Рауса
- •Устойчивость дискретных полиномов
- •Частотные критерии устойчивости замкнутых систем
- •Устойчивость нелинейных систем
- •Операции над множествами
- •1.3. Упорядоченное множество и прямое произведение множеств
- •1.4. Соответствия
- •1.5. Конечные и бесконечные множества. Мощность множества
- •5. Случайные процессы в системах управления
- •5.1. Случайные величины и их основные характеристики
- •5.1.1. Интегральный закон распределения (функция распределения)
- •5.1.2. Дифференциальный закон распределения (плотность вероятности)
- •5.1.3. Моменты случайных величин и их свойства
- •5.2. Векторные случайные величины
- •5.2.1. Функция распределения двумерного случайного вектора
- •5.2.2. Функция плотности вероятности двумерного случайного вектора
- •5.2.3. Моменты системы случайных величин
- •5.3. Случайные функции. Многомерные законы распределения
- •5.4. Характеристики случайных функций
- •5.5. Операции над случайными функциями
- •5.5.1. Суммирование случайной и детерминированной функций
- •5.5.2. Интегрирование случайной функции
- •5.5.3. Дифференцирование случайной функции
- •5.5.4. Сложение случайных функций
- •5.6. Стационарные случайные процессы
- •5.6.1. Эргодическая теорема
- •5.6.2. Корреляционная функция стационарного случайного процесса
- •5.6.3. Расчет корреляционной функции по экспериментальным данным
- •5.7. Спектральная плотность стационарного случайного процесса
- •5.8. Связь между спектральной плотностью и корреляционной функцией стационарного случайного процесса
- •5.9. Случайные функции и их характеристики (примеры)
- •5.10. Прохождение стационарного случайного сигнала через линейную систему
- •Введение
- •Алгоритм нелинейного динамического прогнозирования и некоторые его модификации
- •Интерпретация алгоритма с использованием виртуальных моделей как процедуры ассоциативного поиска
Алгоритм Рауса
Полагаем
![]()
![]()
Полагаем
![]()
(если
![]() ,
то полином неустойчив), пересчитываем
коэффициенты по формулам
,
то полином неустойчив), пересчитываем
коэффициенты по формулам
![]()
и
полагаем
![]() .
.
3.
Если
![]() ,
возвращаемся к пункту 2. Если
,
возвращаемся к пункту 2. Если
![]() ,
то полином устойчив. В остальных случаях
полином неустойчив.
,
то полином устойчив. В остальных случаях
полином неустойчив.
Алгоритму
Рауса часто придают табличную форму:
коэффициенты
![]() ,
полученные
на первом шаге, записывают в первую
строку
таблицы. Каждая последующая
строка содержит на один элемент меньше;
она получается из предыдущей при помощи
пересчета на основе леммы (шаг 2 алгоритма).
В результате получают треугольную
таблицу
Рауса, и
для устойчивости необходимо и достаточно,
чтобы элементы первого столбца таблицы
были положительны (условие
,
полученные
на первом шаге, записывают в первую
строку
таблицы. Каждая последующая
строка содержит на один элемент меньше;
она получается из предыдущей при помощи
пересчета на основе леммы (шаг 2 алгоритма).
В результате получают треугольную
таблицу
Рауса, и
для устойчивости необходимо и достаточно,
чтобы элементы первого столбца таблицы
были положительны (условие
![]() на
шаге 3). Существуют и иные, несколько
более экономные схемы вычислений в
алгоритме Рауса.
на
шаге 3). Существуют и иные, несколько
более экономные схемы вычислений в
алгоритме Рауса.
Существуют и другие алгебраические критерии устойчивости. Самый известный из них — это критерий Гурвица, формулируемый с помощью определителей. Он, однако, гораздо менее удобен с вычислительной точки зрения, чем алгоритм Рауса, и мы на нем останавливаться не будем.
Устойчивость дискретных полиномов
Приведем теперь аналоги этих же условий устойчивости для дискретных систем. Задан полином с вещественными коэффициентами
![]()
нас интересует, когда он является устойчивым по Шуру, т. е. когда его корни находятся вне единичного круга. Аналогом критерия Михайлова является следующий критерий.
Теорема 5.6. Полином ( ) шуровский тогда и только тогда, когда годограф
![]()
не охватывает начала координат.
Действительно,
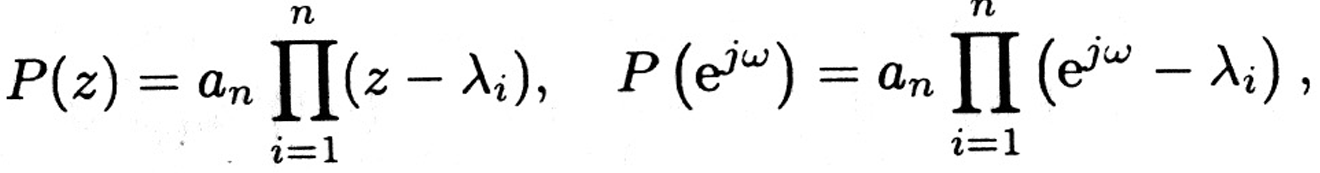
если
![]() находится вне единичного круга, то
приращение аргумента равно нулю, когда
находится вне единичного круга, то
приращение аргумента равно нулю, когда
![]() пробегает единичную окружность. Если
же
пробегает единичную окружность. Если
же
![]() лежит внутри единичного круга, то
приращение аргумента
лежит внутри единичного круга, то
приращение аргумента
![]() равно
равно
![]() ;
таким образом, годограф
;
таким образом, годограф
![]() охватывает начало координат к
раз,
если к
—
число неустойчивых корней
охватывает начало координат к
раз,
если к
—
число неустойчивых корней
![]() .
.
При
пользовании графическими критериями
удобство соглашения относительно корней
устойчивого полинома
![]() налицо: никакого труда не составляет
определить по графику, охватывает ли
кривая начало координат, в то время как
посчитать число оборотов вокруг нуля
бывает сложно или невозможно, например,
если P(z)
= zn.
При
иных подходах бывает проще проверить
принадлежность корней внутренности
единичного круга,
налицо: никакого труда не составляет
определить по графику, охватывает ли
кривая начало координат, в то время как
посчитать число оборотов вокруг нуля
бывает сложно или невозможно, например,
если P(z)
= zn.
При
иных подходах бывает проще проверить
принадлежность корней внутренности
единичного круга,![]() ;
для этого можно воспользоваться следующим
соображением. При
изменении порядка коэффициентов полинома
на обратный,
;
для этого можно воспользоваться следующим
соображением. При
изменении порядка коэффициентов полинома
на обратный,
![]()
его
корни переходят во взаимно обратные:
![]()
Приведем теперь аналог алгоритма Рауса для дискретного случая (называемый дискретным критерием Рауса-Шура). Наряду с полиномом рассмотрим полином с теми же коэффициентами, но записанными в обратном порядке:
![]() (5.17)
(5.17)
и возьмем их линейную комбинацию
![]()
Полином
P(z)
будет
иметь степень
![]() ,
т.е. на единицу меньше степени P(z).
Утверждение,
аналогичное лемме 5.1, заключается в
следующем (приведем его без доказательства).
,
т.е. на единицу меньше степени P(z).
Утверждение,
аналогичное лемме 5.1, заключается в
следующем (приведем его без доказательства).
Лемма 5.2. Если
![]()
и
полином![]() устойчив, то
и
устойчив, то
и
![]() устойчив; в противном случае
устойчив; в противном случае
![]() неустойчив.
неустойчив.
Таким
образом, рекуррентно понижая степень
полинома, придем к полиному первой
степени вида
![]() .
Он устойчив при |
.
Он устойчив при |![]() |
> 1. . sm
самым
получаем простой
алгоритм проверки устойчивости дискретных
полиномов.
|
> 1. . sm
самым
получаем простой
алгоритм проверки устойчивости дискретных
полиномов.
Если
корни P(z)
(3.16)
лежат вне единичного круга, то P(z)
не
меняет знак для
всех
![]() .
С учетом Р(0) = а0
> 0 это дает
.
С учетом Р(0) = а0
> 0 это дает
![]() и
и
![]() .
.
Приходим к следующим простым необходимым условиям устойчивости:
![]()
Отметим еще, что имеется также простое достаточное условие:
![]()
и дискретный полином P(z), удовлетворяющий этому условию, называется сверхустойчивым.
Генерировать устойчивые полиномы можно как на основе леммы 5.2 (применяя ее «в обратном направлении», т.е. повышая степень полиномов), так и пользуясь следующей параметризацией.
Лемма
33. Людой
устойчивый полином P(z)
степени
![]() с Р(0) = 1 может быть получен с помощью
рекуррентной процедуры
с Р(0) = 1 может быть получен с помощью
рекуррентной процедуры
![]()
Числа
tk
иногда
называют параметрами
Фама—Медича. Таким
образюм, каждой точке единичного куба
в
![]() ставится во взаимно однозначное
соответствие устойчивый полином.
ставится во взаимно однозначное
соответствие устойчивый полином.
Таким образом, мы нашли графические и алгебраические критерии устойчивости (гурвицевой и шуровской) для полиномов. Следующим естественным шагом было бы установление таких же критериев для матриц, т.е. способов проверки требуемого расположения собственных значений матрицы без их явного вычисления. К сожалению, такие методы отсутствуют. Единственный известный подход — для заданной матрицы А построить ее характеристический полином P(s) = det (sI — А) (для этого cуществуют эффективные алгоритмы — они совпадают с методами приведения матриц к фробениусовой форме), а затем применить критерии устойчивости полиномов.
