Система управления с обратной связью

Для такой задачи принципиальным является то, какие отклики, т.е. какие сигналы формирует регулятор по совокупности поступающих ему на вход сигналов, несущих информацию о поведении объекта регулирования. В этом смысле для описания системы можно ограничиться только описанием «вход-выход» (2).

Вопрос состоит в том, а сколько существует возможных структур регулятора, т.е. сколько возможных регуляторов для достижения фиксированной цели регулирования. Другими словами, сколько и каких систем (1), характеризующих «внутреннюю сторону» регулятора обеспечивают решение задачи регулирования.

Т.е. если две динамические системы имеют одинаковые реакции на постоянные сигналы или сигналы из определенного частотного диапазона, то это еще не означает, что эти системы имеют одинаковые структуры, определяемые переходной функцией и функцией выхода.

Основные формы представления систем

Описание систем (1), (2) является слишком абстрактным и обобщенным. Обычно для изучения систем и управления используют формы записи, максимально использующие априорные знания о системе с учетом решаемой задачи.

Опреаторная форма представления систем

. (3)

Здесь -l-мерный входной сигнал из множества U, m-мерный выходной сигнал из множества Y.

- оператор, или отображение, который ставит в соответствие каждому сигналу u на входе определенный сигнал y на выходе.

При этом, если подразумевается, что (3) – «внутреннее» описание системы, то оператор некоторым известным образом формализует на каком-либо математическом языке принадлежность всех элементов системы к восьмерке (1).

Если же нужно сделать «внешнее» описание системы, оператор дает формализацию типа (2). Т.е. операторная форма определения системы может применяться для описания как внешней, так и внутренней природы системы.

Описание систем в терминах «вход-выход»

Наиболее распространенным для рассмотрения в теории и на практике является такой класс динамических систем, как линейные стационарные системы.

Для формального описания поведения таких систем используются: в непрерывном случае – различные структуры обыкновенных дифференциальных уравнений, в дискретном случае – разностные уравнения.

Процесс получения дифференциальных уравнений, описывающих поведение системы, основан на использовании четырех основных формализованных элементарных звеньев:

1. Усилительное звено ;

2. суммирующее звено ;

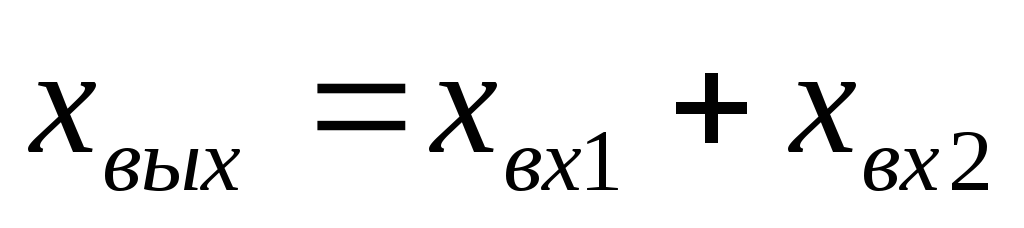3. интегрирующее звено ;

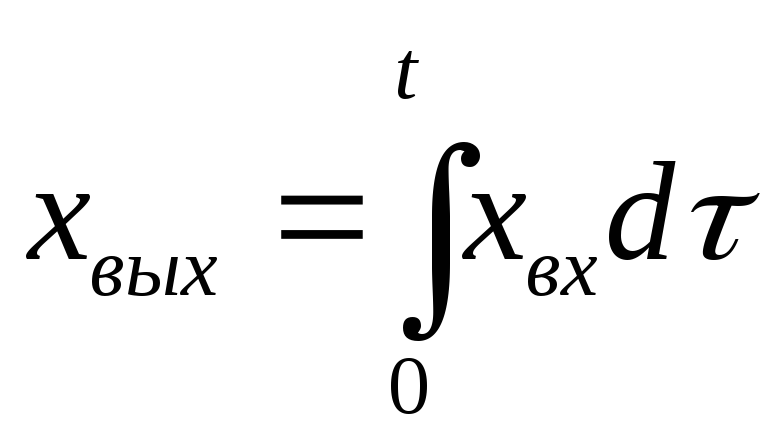4. дифференцирующее звено.

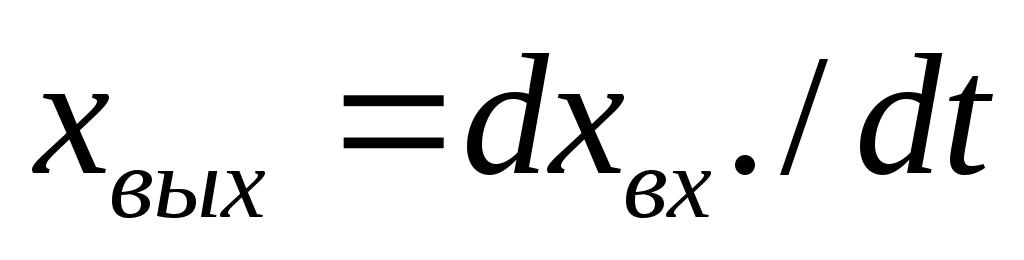Непрерывные модели типа «вход-выход» основаны на использовании дифференциальных уравнений, включающих только входные и выходные сигналы.

Главным достоинством таких моделей является то, что они оперируют с содержательными переменными. Это всегда величины или сигналы, имеющие конкретное (физическое, механическое, электротехническое, химическое и пр. выражение и непосредственно измеряемые либо наблюдаемые. В процессе разработки, преобразования или использования соответствующие модели всегда доступны для содержательного анализа и проверки адекватности.

В результате применения указанных четырех звеньев (зачастую с различными упрощающими предположениями) возникают уравнения, которые применительно к самому общему случаю можно записать в виде:

. (4)

Здесь - вектор выходных величин (сигналов) системы;- вектор входных величин (сигналов) системы;- вещественные матрицы размераmxm, - вещественные матрицы размераmXs.

Причинность, физическая реализуемость систем

При этом предполагается, что входной и выходной сигналы дифференцируемы необходимое число раз, порядок дифференцирования выходного сигнала не ниже, чем входного сигнала. Первое предположение связано с необходимостью применять соответствующий математический аппарат, а второе – с так называемойфизической реализуемостью, или причинностью (казуальностью) системы. Критерий физической реализуемости сводится к утверждению того, что в реальном мире действует так называемый принцип причинности, т.е. следствие не может опережать во времени причину. Систему называют причинно обусловленной, если значение выходного сигнала в произвольный момент времени зависит от значений входных сигналов в более ранние моменты времени до текущего момента времени включительно.

Связь этого принципа с порядком производных в формуле (4) не столь очевидна, как это имеет место в разностных уравнениях, являющихся аналогом (4) в системах с дискретным временем, или, как их называют, дискретных системах.

, гдеn – дискретное время.

Для непрерывного случая: в соответствии с общепринятой методикой решения обыкновенных дифференциальных уравнений выходной сигнал состоит из двух аддитивных (т.е. складываемых) составляющих: вынужденной , обусловленной только входным воздействием, и свободной , обусловленной только наличием ненулевых начальных условий.

Вынужденная составляющая ищется как частное решение уравнения (4) при нулевых начальных условиях. Свободная составляющая уравнения (4) удовлетворяет, как известно, однородному уравнению (с нулевым входным воздействием):

. (5)

Это уравнение получается из (4) при .

Уравнение (5), вообще говоря, имеет неограниченное число решений. Единственное из них определяется заданием так называемых начальных условий, сводящихся к прохождению полного решения через вполне определенную точку. Совокупность начальных условий в общем случае представляет собой матрицу:

, (6)

содержащую значения всех компонент вектора и всех производных довключительно в фиксированный момент времени.

Для краткости (6) можно переписать в виде:

. В верхнем индексе в скобках указан порядок производной.

Передаточная функция

Приведем уравнение (4) к операторной форме путем применения преобразования Лапласа.

Для этого заменим в уравнении (4) символ дифференцирования на комплексное .

Для вынужденной составляющей при условиииз уравнения (4) получаем операторное уравнение:

, (7)

где - полиномиальные матрицы вида:

.

Формулу

можно считать краткой записью формулы:

.

Здесь утверждается, что сигнал есть результат обратного преобразования Лапласа такого изображения, которое является решением алгебраического уравнения (7), в правой части которого стоит преобразование Лапласа от входного сигнала, и все это – при нулевых начальных условиях.

Функцию 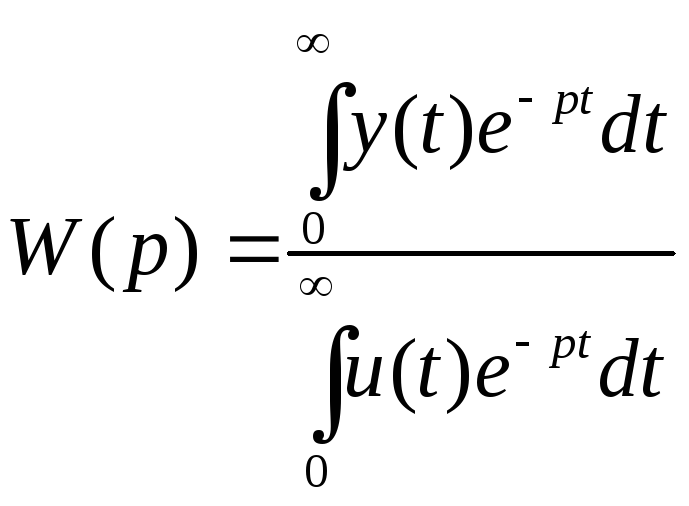называютпередаточной функцией системы (4).

Здесь и- соответствующиепреобразования Лапласа выходной и входной переменных при нулевых начальных условиях.

Несколько сложнее обстоит дело с ненулевыми начальными условиями. Для того, чтобы получить операторную запись и в этом случае, вводят некоторый вспомогательный полином , определяемый начальными условиями (6), и операторное уравнение принимает вид:

.

В дискретном случае полагают формально p=q, где q – оператор единичного запаздывания: .

Метод описания систем в пространстве состояний

считают самым значимым в теории систем. Вообще говоря, пространство состояний, переменные состояния использовались со времен И. Ньютона. На определенном этапе более популярными у исследователей стали модели «вход-выход». Это объясняется большей наглядностью таких моделей и относительной легкостью их интерпретации. В основном это относится к частотным методам и передаточным функциям.

Возрождение интереса к методам описания систем в пространстве состояний связывают с именами Понтрягина, Беллмана, и – в первую очередь – Р. Калмана. Благодаря этому подходу стало возможным изучение таких свойств систем как управляемость, наблюдаемость, достижимость, восстанавливаемость.

Для детерминированной системы под состоянием системы понимают ее некоторую характеристику, содержащую всю информацию о ее прошлом (прошлом состоянии, прошлом воздействии извне), необходимую для однозначного определения ее настоящего и будущего.

По сути, состояние системы в момент - это набор сведений о поведении системы, которого вместе с некоторым возможным входным воздействием, заданным придостаточно для определения выходного сигнала припри любом.

Для систем, описываемых дифференциальными уравнениями первого порядка, начальное условие в момент можно считать состоянием системы в момент.

Рассмотрим в качестве примеров три типа состояний, важных для практического анализа систем.

Примеры состояний

Нулевое состояние – это состояние , обладающее следующим свойством:

Если система находится в нулевом состоянии

,

и входное воздействие при всех,

то выходной сигнал системы:

при всех.

Такое состояние необязательно единственное.

Установившееся состояние (если оно существует) есть такое единственное состояние, в которое система приходит при нулевом входном воздействии независмо от начального состояния.

Состояние равновесия – это некоторое состояние (не обязательно нулевое), в котором система остается при нулевом входном воздействии при всех .

Формально задать систему в пространстве состояний означает сформулировать общие правила построения системы (1) с описанием ее внутренней структуры, т.е. пространства состояний X и двух функций (переходной и выходной) по описанию ее внешнего поведения (2).

Основные свойства систем

В общем случае для систем введены две пары различных понятий: управляемость и достижимость, с одной стороны, и наблюдаемость и идентифицируемость, с другой.

Р.Калман предлагает различать задачи наблюдения – когда текущее состояние x(t) определяется по выходным величинам в будущем иидентификации – когда текущее состояние x(t) определяется по выходным величинам в прошлом. В некотором смысле понятие идентифицируемости состоянияx(t) естественным образом дополняет понятие управляемости, а понятие наблюдаемости – понятие достижимости. Поэтому обычно ограничиваются понятиями управляемости и наблюдаемости.

Определения управляемости и наблюдаемости

Система (1) называется полностью управляемой тогда и только тогда, когда для каждого состояния в фиксированный момент временинайдется входное воздействие, переводящее систему изв начало координат.

Система (1) называется полностью наблюдаемой тогда и только тогда, когда каждому значению в фиксированный момент времениможно поставить в соответствие,.

Описание в пространстве состояний линейных систем

Существует теорема [4], которая утверждает, что каждая конечномерная гладкая линейная динамическая система (1) с непрерывным временем описывается уравнениями:

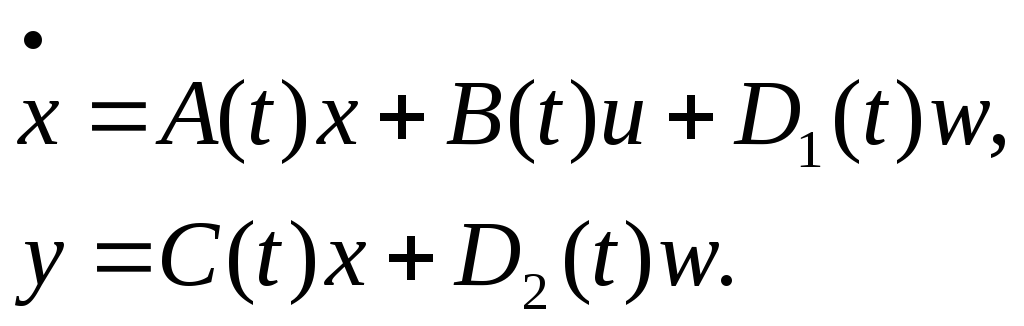(8)

Здесь и далее - начальное условие. Справедлива и обратная теорема.

Матрицы - матрицы коэффициентов, являющиеся в общем случае функциями времени.

Стационарные линейные системы

Далее рассмотрим более узкий класс, частный случай систем (8), когда матрицы не зависят от времени, т.е.

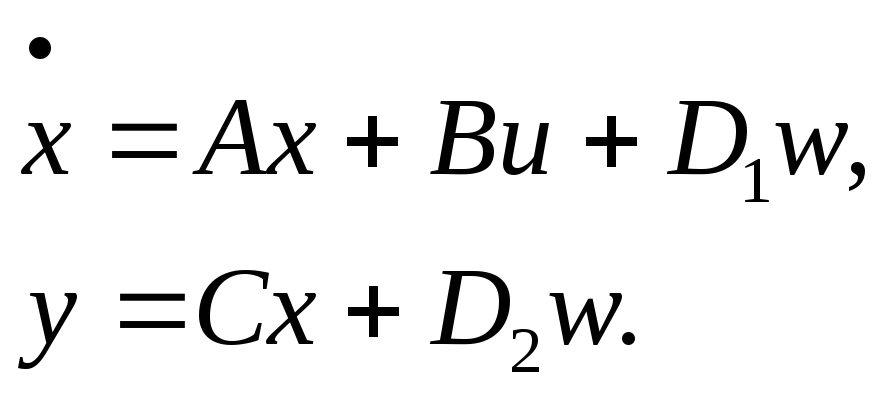(9)

Такие линейные системы называются стационарными. Описание таких систем в пространстве состояний состоит в выборе четверки постоянных матриц по описанию и.

Иногда этим матрицам дают такие названия: - матрица собственной динамики системы;- матрица эффективностей управляющих воздействий;С – матрица наблюдения системы; - матрицы непосредственного воздействия на выход системы.

Обычно предполагается, что проектировщик знает лишь выход системы . В некоторых случаях, т.е. известно и состояние системы.

Относительно внешних воздействий могут делаться самые разнообразные предположения. Они могут отсутствовать или быть полностью известными; могут быть детерминированными и ограниченными, а могут быть случайными с заданными вероятностными свойствами. Более подробно классы возможных возмущений будут рассмотрены ниже.

Целью управления является выбор таких или, которые придают системе заданные свойства: устойчивость, оптимальность по определенному критерию качества и т.д.

Система, в которой управление отсутствует, может быть записана в виде:

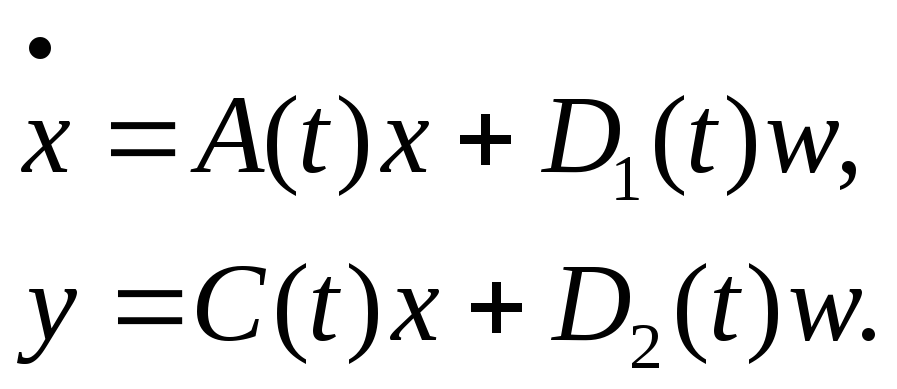(10)

Такие системы называются открытыми.

Отметим, что если в (9) управление уже выбрано (либо в форме- т.нпрограммное управление, открытая система с программным управлением, либо в виде - в форме обратной связи), то мы получаем уравнение типа (10), но:

• с иным внешним возмущением, равным 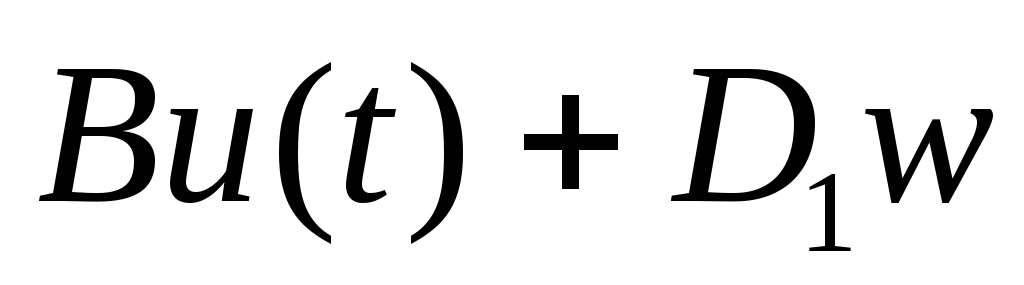, если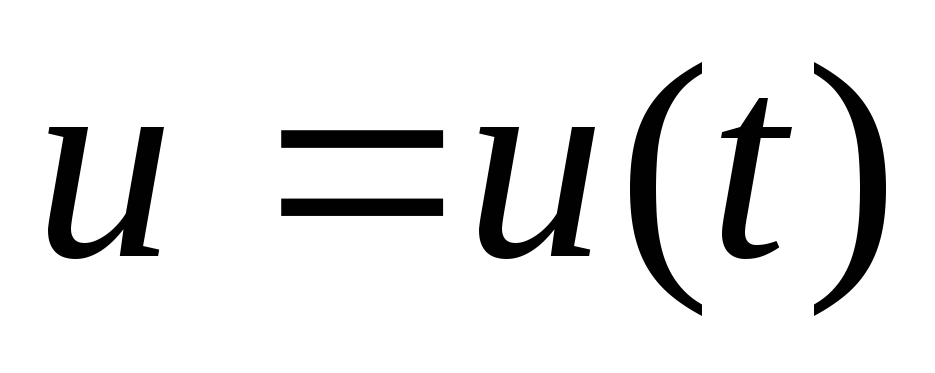либо

• с другой матрицей , т.е.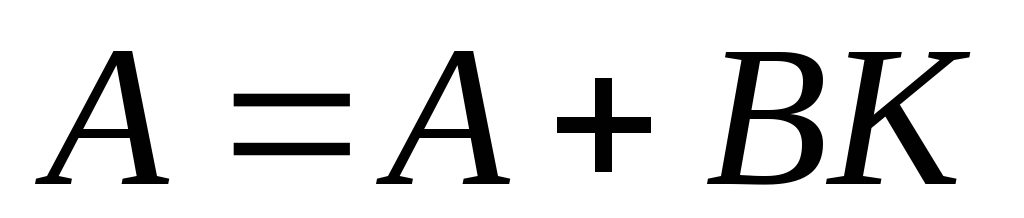- если.

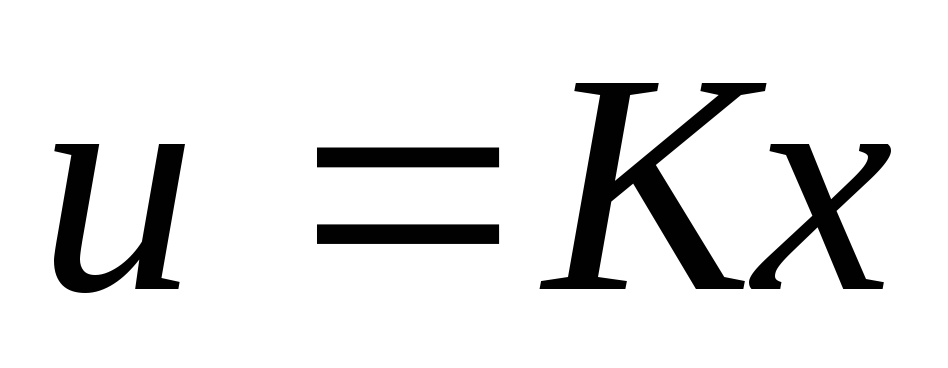В последнем случае говорят о замкнутой системе.

Решение открытой системы (10) может быть записано в явном виде:

(11)

Здесь в начальный момент времени, а- матричная экспонента.

Приведем некоторые вспомогательные понятия и положения.

Определение. Матричная экспонента. Поскольку функция непрерывна и дифференцируема, то она представима в виде ряда:

Приведем основные свойства этой функции.

1. .

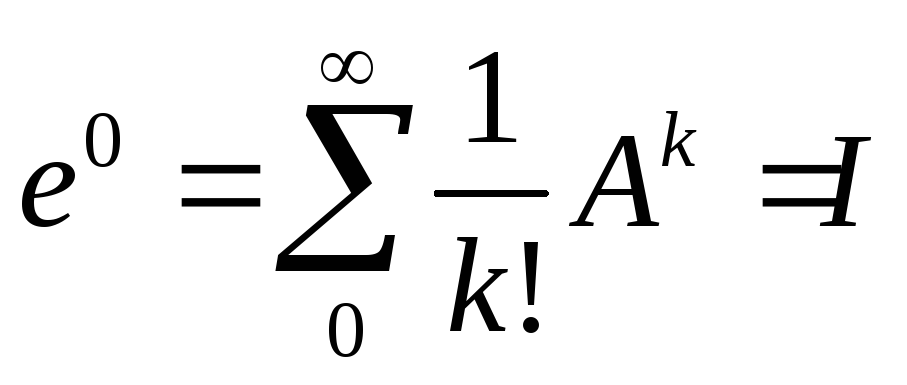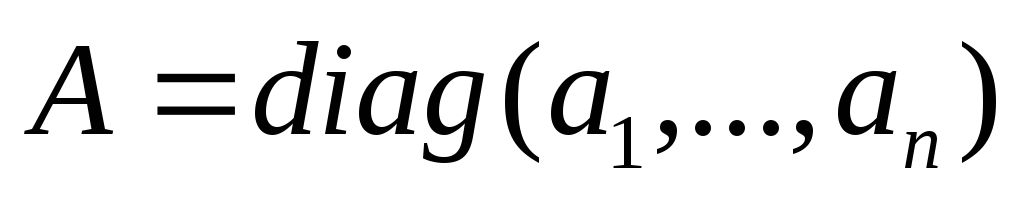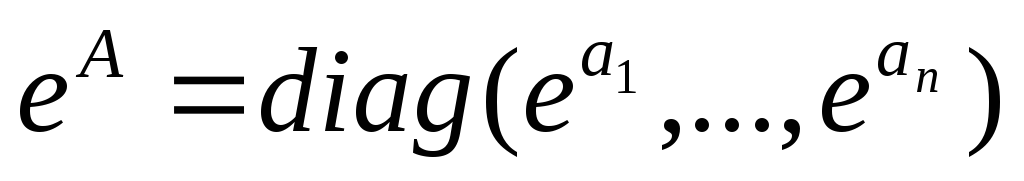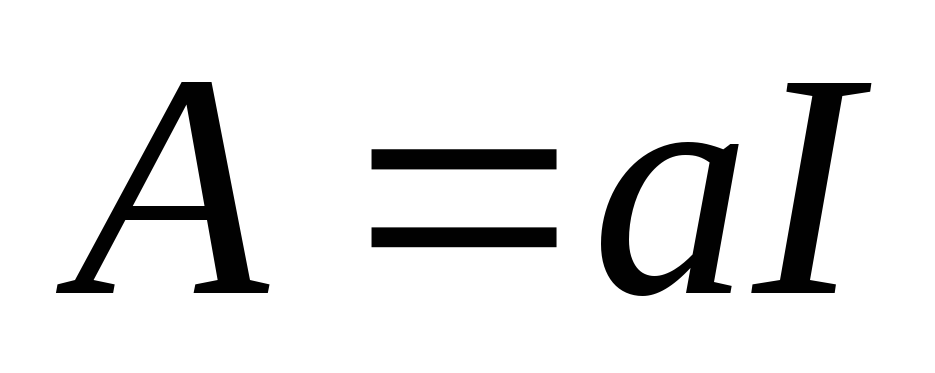2. Если , то. В частности, если, то.

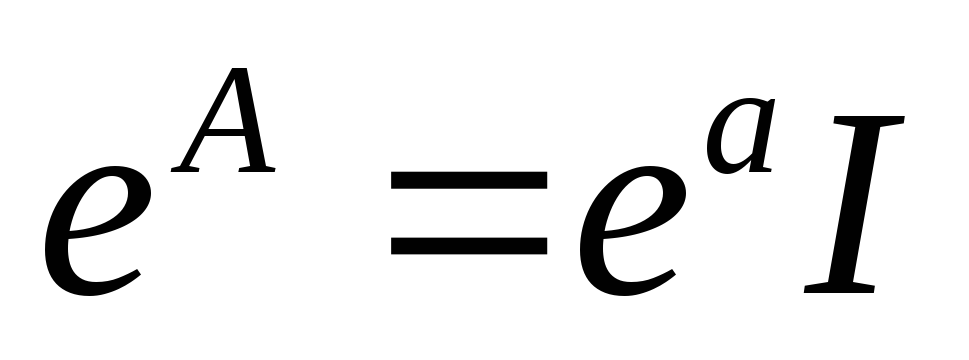3. Если матрицы и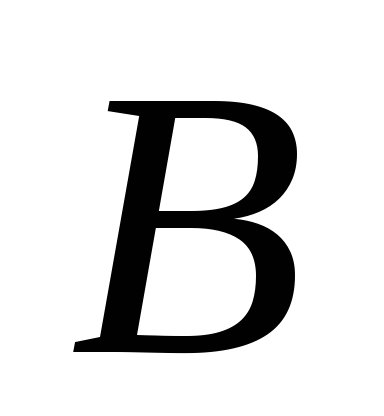коммутируют, т.е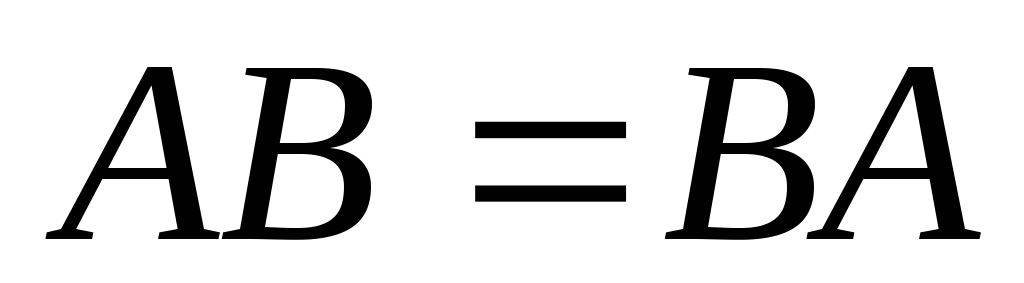, то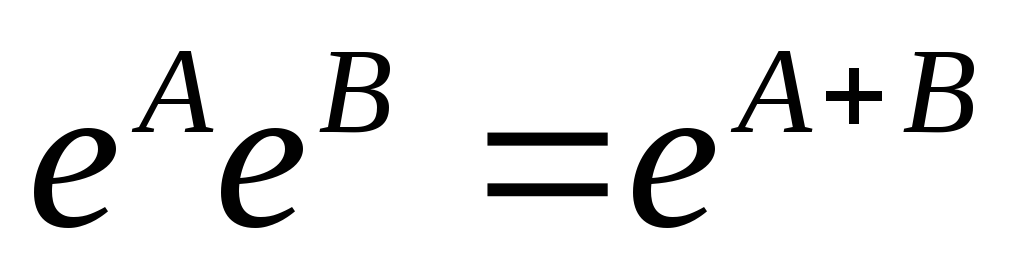. Обратное, вообще говоря, неверно. С другой стороны, если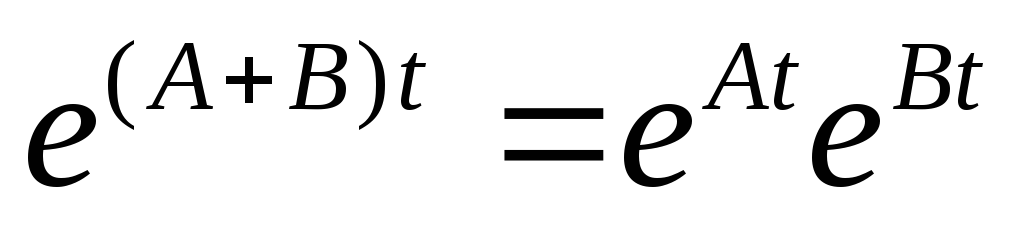для всех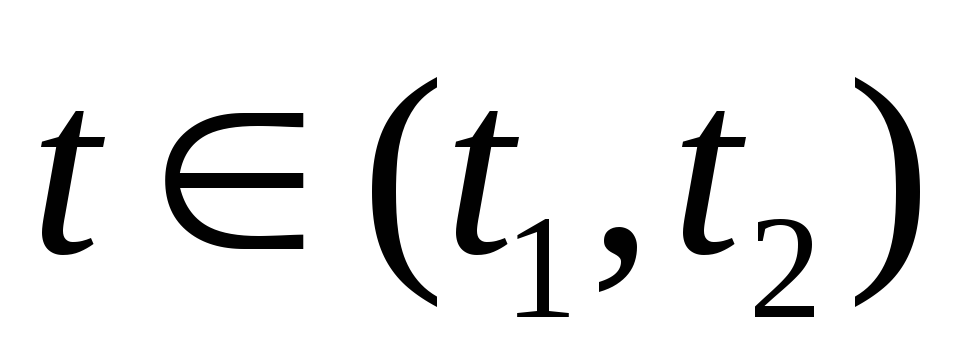, то.

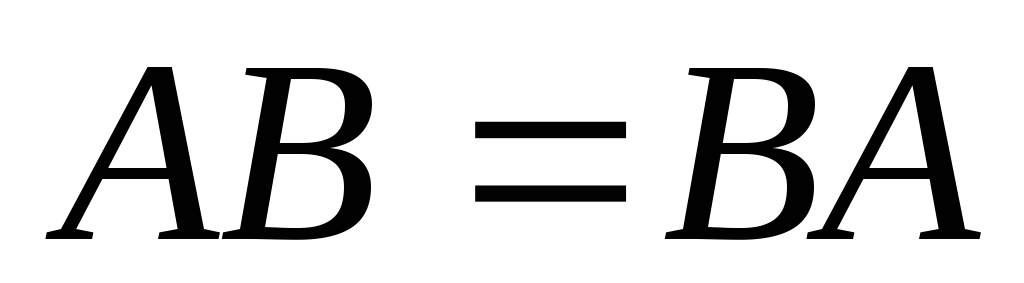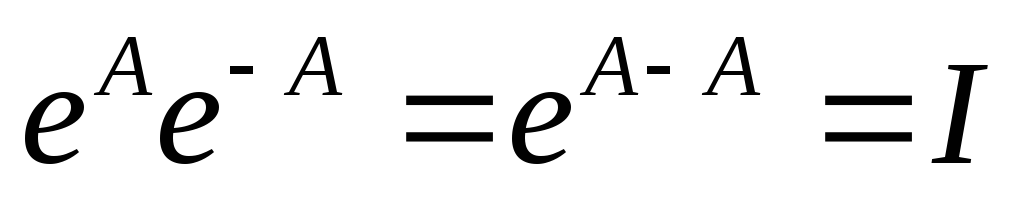4. . Поэтому, в частности, 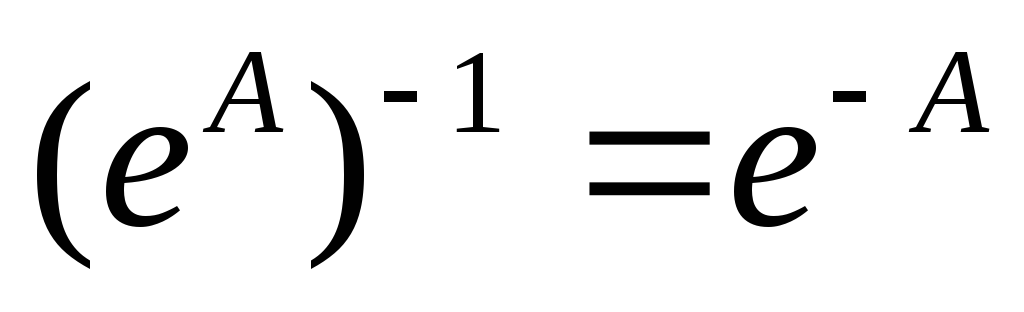для любой матрицы.

5. .

6. .

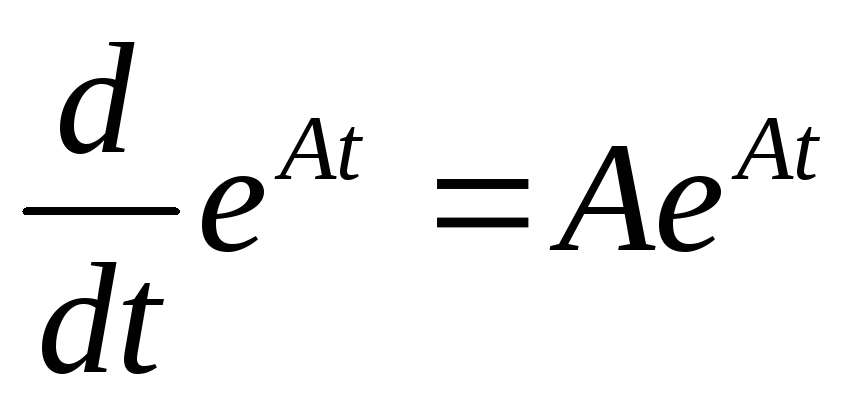7. Если матрица обратима, то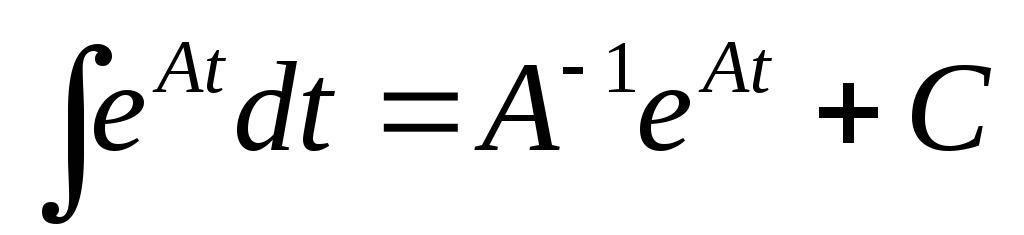, где- некоторая постоянная матрица. В частности,, и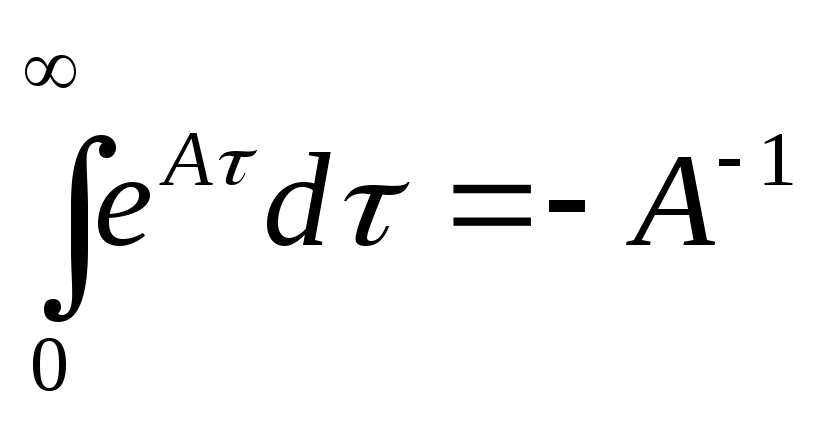.