
- •Речевая система
- •Система управления с обратной связью
- •Вернемся к выражению (11) для решения системы (10). Если в этом выражении иизвестны, то можно найтидля всех моментов.
- •Пусть в системе, представленной линейной моделью в пространстве состояний
- •Устойчивость систем
- •Устойчивость линейных непрерывных систем
- •Устойчивость линейных дискретных систем.
- •Критерии устойчивости полиномов
- •Графические критерии устойчивости полиномов Пусть задан полином
- •Алгоритм Рауса
- •Устойчивость дискретных полиномов
- •Частотные критерии устойчивости замкнутых систем
- •Устойчивость нелинейных систем
- •Операции над множествами
- •1.3. Упорядоченное множество и прямое произведение множеств
- •1.4. Соответствия
- •1.5. Конечные и бесконечные множества. Мощность множества
- •5. Случайные процессы в системах управления
- •5.1. Случайные величины и их основные характеристики
- •5.1.1. Интегральный закон распределения (функция распределения)
- •5.1.2. Дифференциальный закон распределения (плотность вероятности)
- •5.1.3. Моменты случайных величин и их свойства
- •5.2. Векторные случайные величины
- •5.2.1. Функция распределения двумерного случайного вектора
- •5.2.2. Функция плотности вероятности двумерного случайного вектора
- •5.2.3. Моменты системы случайных величин
- •5.3. Случайные функции. Многомерные законы распределения
- •5.4. Характеристики случайных функций
- •5.5. Операции над случайными функциями
- •5.5.1. Суммирование случайной и детерминированной функций
- •5.5.2. Интегрирование случайной функции
- •5.5.3. Дифференцирование случайной функции
- •5.5.4. Сложение случайных функций
- •5.6. Стационарные случайные процессы
- •5.6.1. Эргодическая теорема
- •5.6.2. Корреляционная функция стационарного случайного процесса
- •5.6.3. Расчет корреляционной функции по экспериментальным данным
- •5.7. Спектральная плотность стационарного случайного процесса
- •5.8. Связь между спектральной плотностью и корреляционной функцией стационарного случайного процесса
- •5.9. Случайные функции и их характеристики (примеры)
- •5.10. Прохождение стационарного случайного сигнала через линейную систему
- •Введение
- •Алгоритм нелинейного динамического прогнозирования и некоторые его модификации
- •Интерпретация алгоритма с использованием виртуальных моделей как процедуры ассоциативного поиска
Устойчивость систем
В этой главе исследуется важнейшее понятие теории систем - понятие устойчивости. Приводятся различные критерии устойчивости как алгебраические, так и графические.
Для нелинейных нестационарных систем имеется множество определений устойчивости: устойчивость точки равновесия и устойчивость движения; устойчивость по Ляпунову и асимптотическая устойчивость; устойчивость «в малом» и «в большом»; устойчивость по начальным условиям и по возмущению.
Для линейных стационарных систем все эти определении совпадают, и мы будем говорить просто об устойчивости.
Устойчивость линейных непрерывных систем
Начнем с простейшей ситуации — открытой невозмущенной системы в пространстве состояний.
Невозмущенные системы
Линейная непрерывная система
![]()
![]() , (5.1)
, (5.1)
где
![]() - матрица
- матрица
![]() ,
не зависящая от
,
не зависящая от
![]() ,
называется
устойчивой,
если
,
называется
устойчивой,
если
![]() при
при
![]() для
любого
для
любого
![]() .
.
Теорема
5.1.
Для
устойчивости системы (5.1)
необходимо
и достаточно, чтобы все собственные
значения
![]() матрицы
матрицы
![]() лежали
в левой полуплоскости:
лежали
в левой полуплоскости:
![]()
![]() .
(5.2)
.
(5.2)
При
этом для всякого
![]() существует
такое
существует
такое![]() ,
что
,
что
![]() .
.
Отметим,
что матрица![]() ;
удовлетворяющая
условиям (5.2), в дальнейшем называется
гурвицевой
или
устойчивой.
Соответственно,
собственное значение с отрицательной
вещественной частью также будем называть
устойчивым.
Если
;
удовлетворяющая
условиям (5.2), в дальнейшем называется
гурвицевой
или
устойчивой.
Соответственно,
собственное значение с отрицательной
вещественной частью также будем называть
устойчивым.
Если
![]() устойчива,
то величина
устойчива,
то величина
![]() называется степенью
устойчивости
(матрицы
или соответствующей системы). По сути,
это минимальное из расстояний от
собственных значений устойчивой матрицы
до мнимой оси.
называется степенью
устойчивости
(матрицы
или соответствующей системы). По сути,
это минимальное из расстояний от
собственных значений устойчивой матрицы
до мнимой оси.
Доказательство.
Необходимость.
Пусть
условие (5.2) не выполнено, т.е. найдется
некоторое собственное значение матрицы
![]() ,
например,
,
например,
![]() такое, что
такое, что
![]()
Если
![]() вещественно, то возьмем в качестве
начального условия
вещественно, то возьмем в качестве
начального условия
![]() ,
где
,
где
![]() - вещественный вектор и
- вещественный вектор и
![]() .
Тогда решение с таким начальным условием
имеет вид
.
Тогда решение с таким начальным условием
имеет вид
![]() ,
и потому
,
и потому
![]() при
при
![]() .
.
Если
![]() — комплексное число
— комплексное число
![]() ,
то
найдется и сопряженное собственное
значение
,
то
найдется и сопряженное собственное
значение
![]() .
Причем,
если
.
Причем,
если
![]() —
собственный вектор, отвечающий
—
собственный вектор, отвечающий
![]()
![]()
![]() ,
то
,
то
![]() — собственный вектор, отвечающий
— собственный вектор, отвечающий
![]() .
При
этом
.
При
этом
![]()
![]() .
.
Возьмем
![]() где
где
![]() ,
тогда
,
тогда
![]() oстается
в том же двумерном подпространстве:
oстается
в том же двумерном подпространстве:
![]() где
где
![]() описываются
дифференциальными уравнениями
описываются
дифференциальными уравнениями
![]()
Обозначая
![]() ,
легко
получаем
,
легко
получаем
![]() ,
т.е.
,
т.е.
![]() при
при
при
при
![]() .
и
.
и
![]() .
.
Достаточность. В силу важности теоремы дадим несколько доказательств достаточности; каждое использует технику, которая неоднократно будет применяться в дальнейшем. При этом в ряде случаев доказательство не будет исчерпывающе строгим — для нас важна главным образом идея, заложенная в нем.
Вспомогательные определения и свойства.
Для любой матрицы
 размерности
размерности
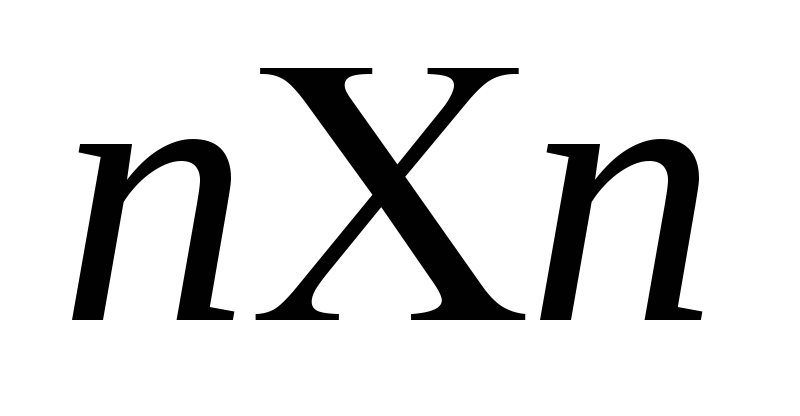 существует
невырожденная матрица
существует
невырожденная матрица
 той же размерности , такая, что
той же размерности , такая, что
![]() ,
где
,
где
![]()
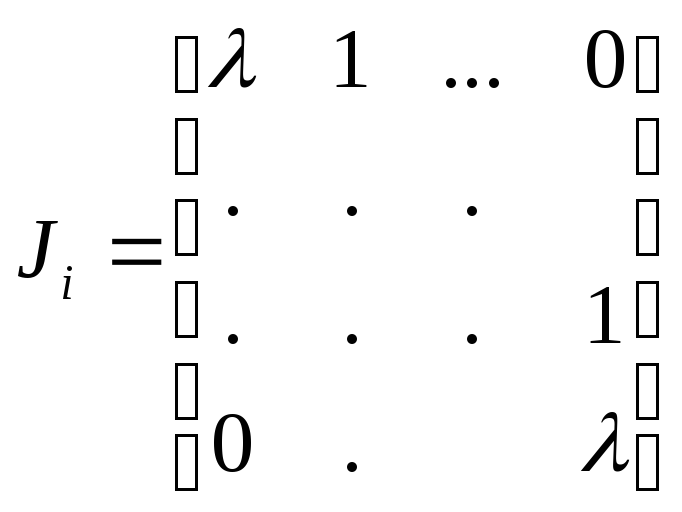 .
.
При
этом
![]() называют преобразованием подобия.
называют преобразованием подобия.
Если все собственные числа квадратной матрицы
 различны, то она приводится преобразованием
подобия к диагональному виду.
различны, то она приводится преобразованием
подобия к диагональному виду.Если при этом
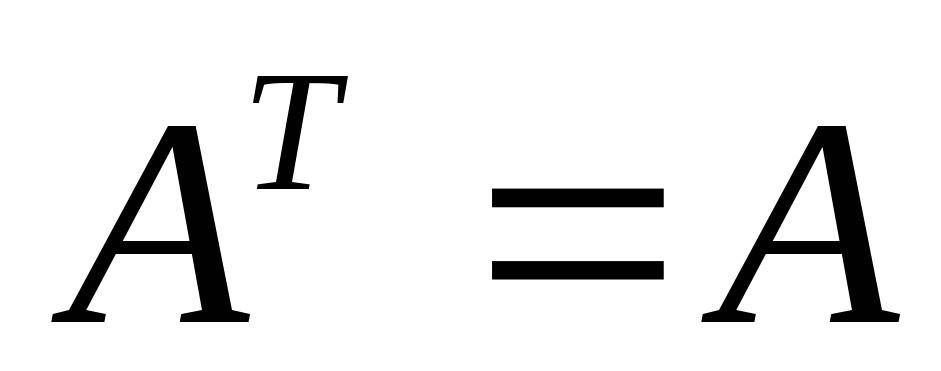 ,
то эта матрица приводится к диагональному
виду вещественным ортогональным
преобразованием подобия
,
то эта матрица приводится к диагональному
виду вещественным ортогональным
преобразованием подобия
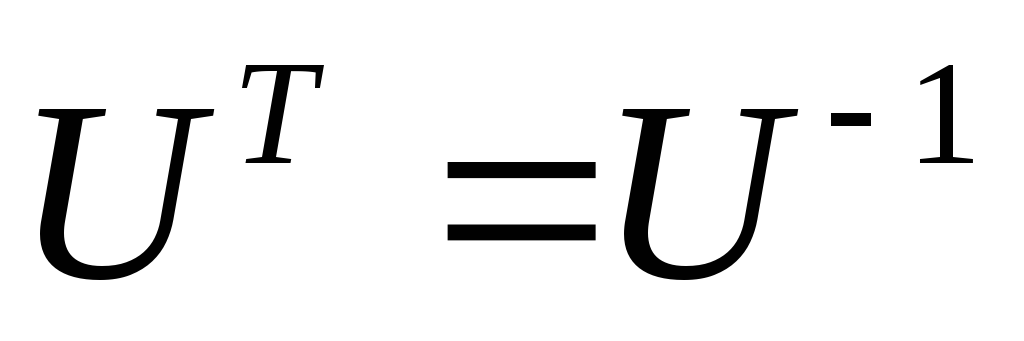 и
и
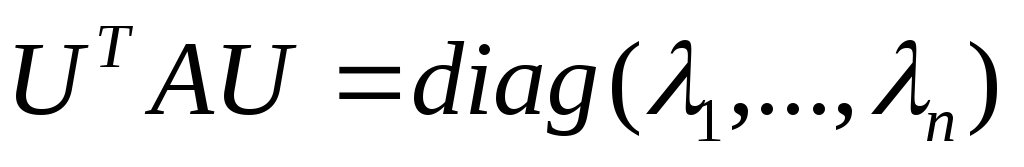 и все ее собственные числа вещественны.
и все ее собственные числа вещественны.Если для квадратной матрицы размерности
 найдется вектор размерности
найдется вектор размерности
такой,
что векторы
![]() линейно независимы, то ее можно привести
с помощью некоторого невырожденного
преобразования подобия к канонической
форме Фробениуса:
линейно независимы, то ее можно привести
с помощью некоторого невырожденного
преобразования подобия к канонической
форме Фробениуса:
 .
.
Характеристический
полином этой матрицы можно выразить
через элементы последней строки:
![]() .
.
Для квадратных матриц введено понятие нормы. Функция
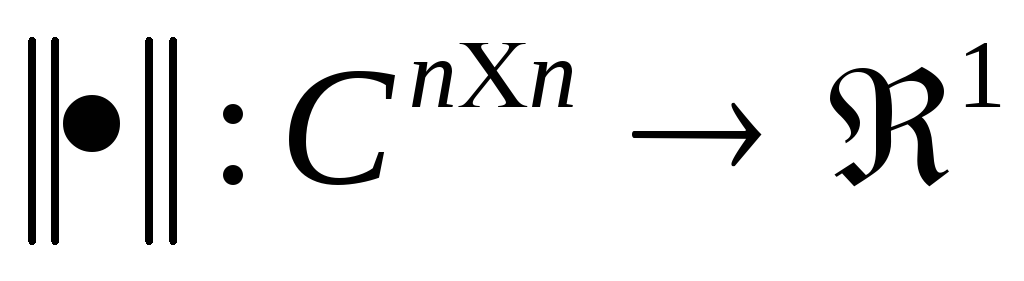 называется матричной
нормой,
если для любых матриц
называется матричной
нормой,
если для любых матриц
 выполнены аксиомы:
выполнены аксиомы:
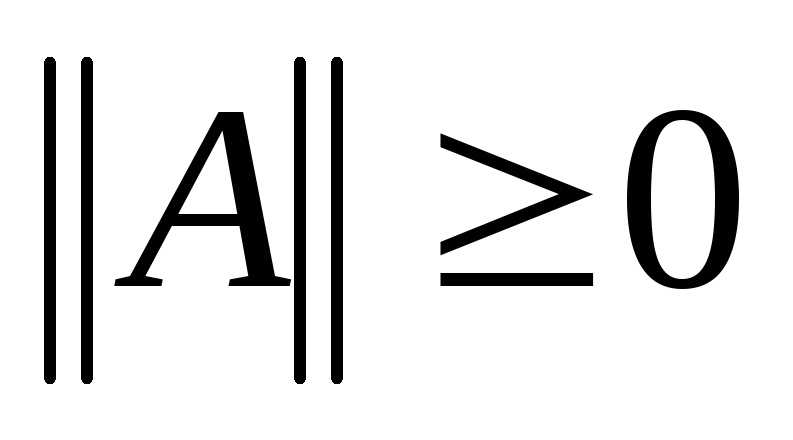 .
.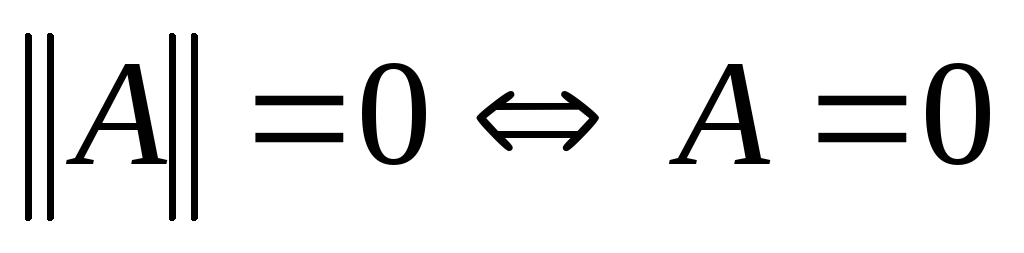 .
.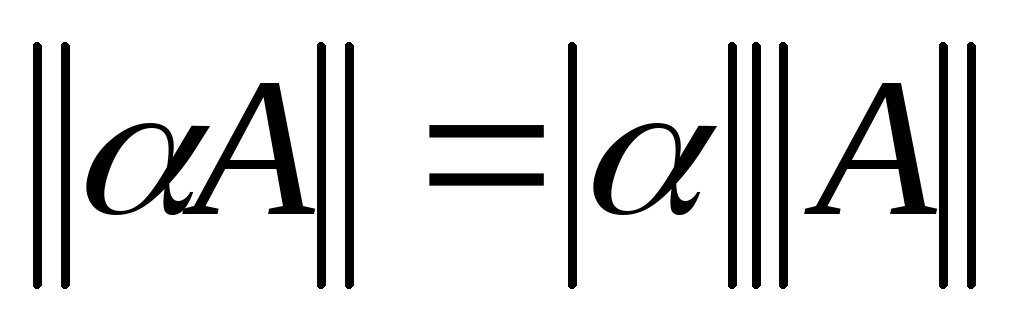 для
любого вещественного
для
любого вещественного
 .
. .
.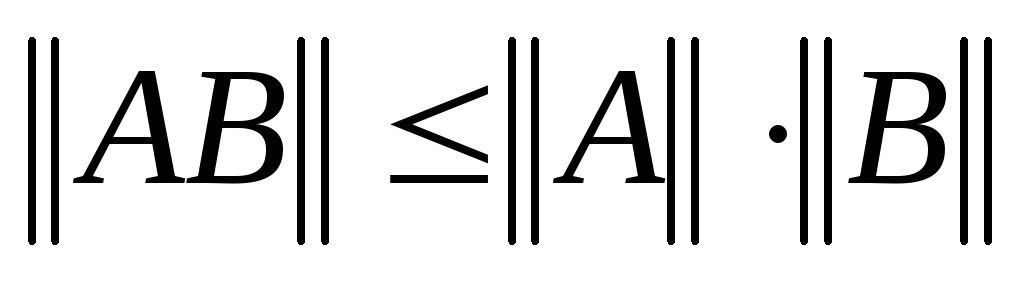 .
.
Мы будем пользоваться т.н. спектральной нормой матриц (хотя существуют и другие):
![]() .
Здесь
.
Здесь
![]() -эрмитово-сопряженная
матрица, т.е. транспонированная и с
комплексно-сопряженными элементами.
-эрмитово-сопряженная
матрица, т.е. транспонированная и с
комплексно-сопряженными элементами.
Доказательство достаточности 1 (оценка матричной экспоненты). Пусть матрица А диагонализируема, т.е. ее можно путем элементарных преобразований привести к диагональному виду. Это возможно, например, если все ее собственные значения различны), т. е. существует такая невырожденная матрица Т, что
![]()
![]()
В этом случае имеем
![]()
что
и доказывает оценку (5.3) для устойчивой
матрицы
![]() (в
этом случае
(в
этом случае
![]() причем можно взять
причем можно взять
![]() ,
а константа
,
а константа
![]() выписывается
явно:
выписывается
явно:
![]()
![]() .
.
В матричной форме результат можно записать как оценку матричной экспоненты:
![]() ,
,
![]()
![]() . (5.4)
. (5.4)
Случай
диагонализируемой матрицы особенно
прост потому, что сделав замену переменной
![]() ,
мы приводим систему к виду
,
мы приводим систему к виду
![]()
![]() ,
,
или,
иначе говоря,
![]() ,
т.е. (5.1) распадается на
,
т.е. (5.1) распадается на
![]() независимых уравнений с решениями:
независимых уравнений с решениями:
![]()
![]() . (5.5)
. (5.5)
Если
![]() ,
и все
,
и все
![]() ,
то
,
то
![]() ,
и
,
и
![]() для
всех
для
всех
![]() ,
поэтому
,
поэтому
![]() .
.
В общем случае матрица А приводится преобразованием подобия не к диагональной, а к блочной жордановой форме:
![]()
![]() .
.
В
этом случае система рассматривается
как
![]() независимых подсистем, соответствующим
блокам
независимых подсистем, соответствующим
блокам
![]() .
Для
одного жорданового блока
.
Для
одного жорданового блока
![]() размерности
размерности![]()

имеем
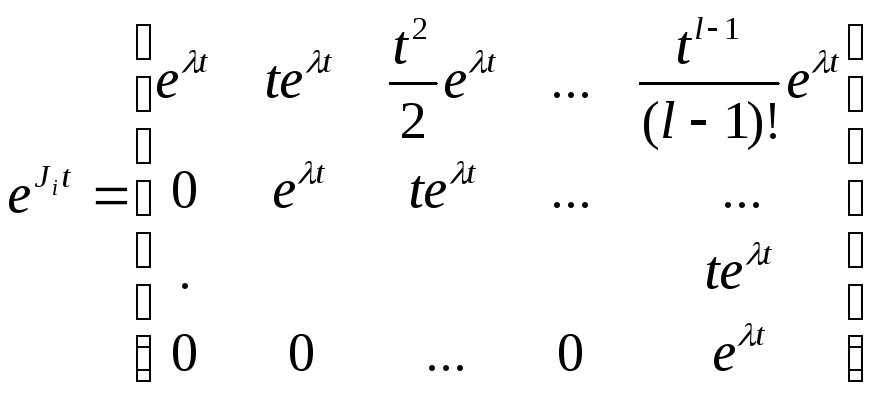 =
=
=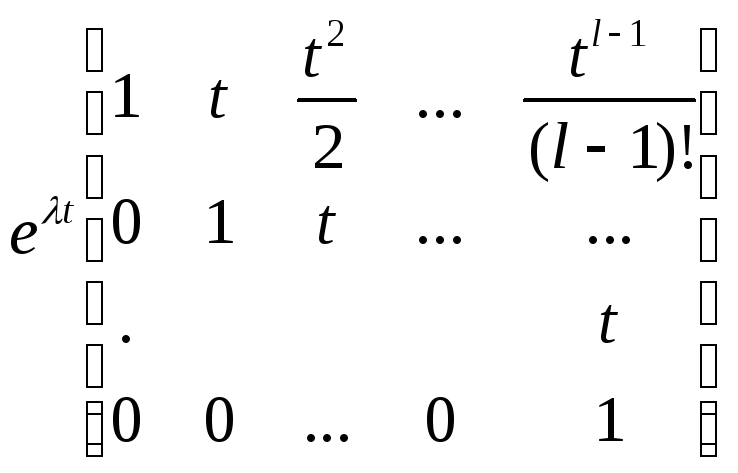
поэтому
если
![]() то найдется полином
то найдется полином
![]() степени
степени
![]() такой, что
такой, что
![]() ,
,
для
любого
![]() .
Здесь
.
Здесь
![]() .
Учитывая
.
Учитывая
![]() ,
приходим к оценке (5.3).
,
приходим к оценке (5.3).
Доказательство достаточности 2 (построение функции Ляпунова).
Рассмотрим
уравнение (относительно некоторой
матрицы
![]() )
следующего вида:
)
следующего вида:
![]() , (5.6)
, (5.6)
![]() —
устойчивая матрица, a
—
устойчивая матрица, a
![]() —
некоторая положительно определенная
матрица; это уравнение называется
матричным
уравнением Ляпунова.
—
некоторая положительно определенная
матрица; это уравнение называется
матричным
уравнением Ляпунова.
Известно, что при сделанных предположениях (А устойчива, Q > 0) оно имеет единственное решение Р > 0.
Построим теперь квадратичную функцию Ляпунова:
![]()
и
покажем, что она монотонно убывает на
решениях
![]() уравнения
(5.1). Запись
уравнения
(5.1). Запись
![]() означает
дифференцированиеV(x(t))
пo
t.
Имеем:
означает
дифференцированиеV(x(t))
пo
t.
Имеем:
![]()
![]() ,
,
где
![]() - наименьшее собственное значение
- наименьшее собственное значение
![]() ,
а
,
а
![]() - наибольшее собственное значение
- наибольшее собственное значение
![]() .
Таким образом, для
.
Таким образом, для
![]() имеем:
имеем:
![]() ,
,
![]()
![]() .
.
Откуда следует
![]()
и
![]() ,
,
где
![]() - наименьшее собственное значение
- наименьшее собственное значение
![]() .
.
Таким образом,
![]() ,
,
![]() ,
,
![]() .
.
Т.е.
мы получили экспоненциальную оценку
типа (5.3) для решений уравнения (5.1). При
этом показатель экспоненты
![]() не связан напрямую с величиной
не связан напрямую с величиной
![]() ,
а выражается через максимальные и
минимальные собственные значения матриц
Р
и
Q
в
уравнении Ляпунова. Можно показать, что
для матрицы
,
а выражается через максимальные и
минимальные собственные значения матриц
Р
и
Q
в
уравнении Ляпунова. Можно показать, что
для матрицы
![]() с
с
![]() справедливо
справедливо
![]() .
.
Итак, теорема 5.1 дает условия устойчивости для невозмущенной системы, заданной в пространстве состояний.
Частотные критерии устойчивости систем, описываемых с помощью передаточных функций
Рассмотрим простейшую одномерную систему
![]()
![]() ,
,
![]() , (5.7)
, (5.7)
где P(s) — полином от оператора дифференцирования s = d/dt:
![]() .
.
Эта система задана с помощью передаточной функции; сформулируем для нее определения и условия устойчивости, которые понадобятся нам в дальнейшем; при этом используем переход к описанию в пространстве состояний.
Определение.
Система (5.7), заданная с помощью пеедаточной
функции, называется устойчивой,
если
![]() ,
,
![]() .
.
Можно доказать, что такая система эквивалентна системе, записанной в пространстве состояний:
![]()
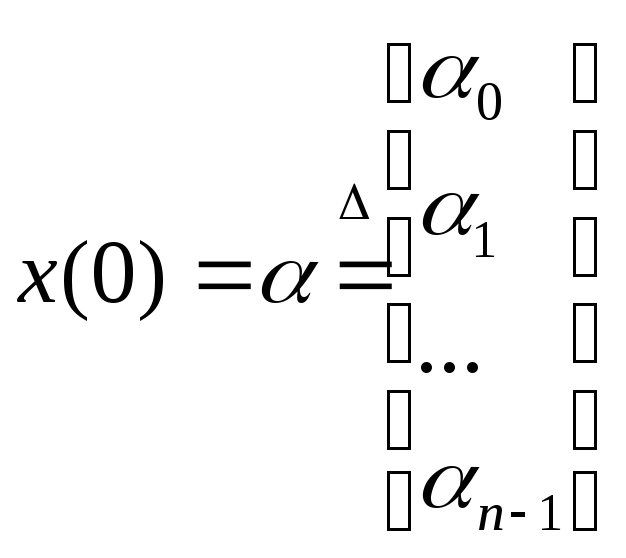 ,
,
 ,
,
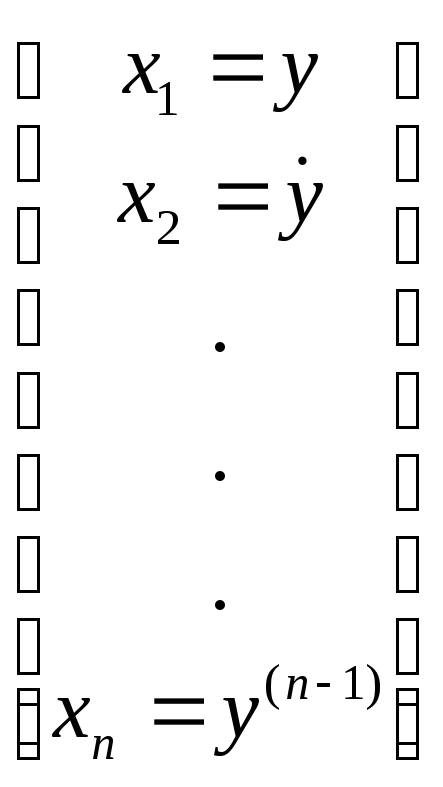 ,
,
с
помощью матрицы
![]() ,
записанной в канонической («фробениусовой»)
форме.
,
записанной в канонической («фробениусовой»)
форме.
Характеристический полином такой матрицы совпадает с P(s), поэтому ее собственные значения — корни P(s). Таким образом, теорема 5.1 приводит к следующему результату.
Теорема 5.2. Для того, чтобы система (5.7) была устойчива, необходимо и достаточно, чтобы все корни полинома P(s). лежали в левой полуплоскости:
![]() ,
,
![]()
Такие полиномы мы будем называть гурвицевыми или устойчивыми, |равно как и соответствующие им системы (5.7).
Возмущенные системы
Рассмотрим теперь систему вида:
![]() (5.8)
(5.8)
Теорема
5.3.
Для
того, чтобы решение системы (5.8) при
![]() было ограниченным при всех ограниченных
внешних воздействиях
было ограниченным при всех ограниченных
внешних воздействиях
![]() ,
необходимо и достаточно, чтобы матрица
,
необходимо и достаточно, чтобы матрица
![]() была устойчива.
была устойчива.
Доказательство. Необходимость. Пусть условие 5.2 не выполнено, т.е.
![]() для некоторого собственного значения
для некоторого собственного значения
![]() и соответствующего собственного
вектора:
и соответствующего собственного
вектора:
![]() ,
,
![]() .
.
Если
![]() вещественно, то возьмем
вещественно, то возьмем![]() ,
тогда
,
тогда
![]()
при
![]() ,
поэтому
,
поэтому
![]()
![]() при
при
![]() .
.
Если
же
![]() ,
то
,
то
![]() ,
т.е. и в этом случае
,
т.е. и в этом случае
![]() при
при
![]() .
.
Если
![]() - комплексное, т.е.
- комплексное, т.е.
![]() ,
,
![]() ,
то
уравнение движения на двумерной
плоскости, порожденной векторами
,
то
уравнение движения на двумерной
плоскости, порожденной векторами
![]() и
и
![]() ,
имеет вид:
,
имеет вид:
![]() ,
,
![]() ,
,
где
![]() тогда для
тогда для![]() имеем
имеем
![]() .
.
Если
выбрать
![]() ,
,
![]() (где
(где
![]() ).
Тогда
).
Тогда
![]() и
и
![]() неограниченно возрастает, т.е. и в этом
случае можно так выбрать ограниченное
внешнее воздействие
неограниченно возрастает, т.е. и в этом
случае можно так выбрать ограниченное
внешнее воздействие
![]() ,
что
,
что
![]() при
при
![]() .
.
Доказательство достаточности аналогично доказательству предыдущей теоремы.
Таким
образом, мы получили, что гурвицевость
матрицы
![]() необходима и достаточна для того, чтобы
решение невозмущенной системы стремилось
к нулю при любом начальном приближении
и чтобы решение возмущенной системы
оставалось ограниченным для ограниченных
возмущений.
необходима и достаточна для того, чтобы
решение невозмущенной системы стремилось
к нулю при любом начальном приближении
и чтобы решение возмущенной системы
оставалось ограниченным для ограниченных
возмущений.
Первое свойство иногда называют устойчивостью по начальному приближению, второе – устойчивостью по входу.
