Вернемся к выражению (11) для решения системы (10). Если в этом выражении иизвестны, то можно найтидля всех моментов.

Дискретные линейные системы

Наряду с непрерывными системами будем рассматривать дискретные линейные системы, описываемые разностными уравнениями.

. (12)

Индекс играет роль времени (дискретное время), а смысл всех остальных векторов и матриц тот же. Дискретные системы могут возникать как при дискретной аппроксимации непрерывных систем, так и в других случаях. Например,может означать номер итерации в итерационном процессе или время в дискретных процессах, связанных с цифровым управлением.

Открытая дискретная система принимает вид:

(13)

а ее решение также выписывается в явной форме:

. (14)

Пример. Модель стационарной линейной системы в пространстве состояний.

Рассмотрим систему дифференциальных первого порядка и алгебраических уравнений

,

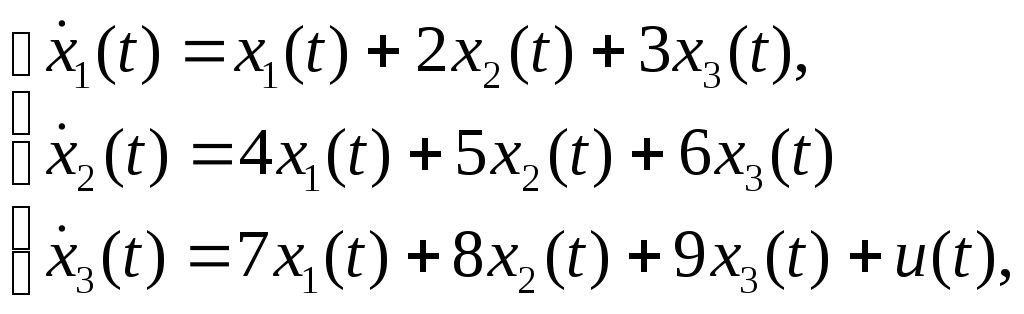
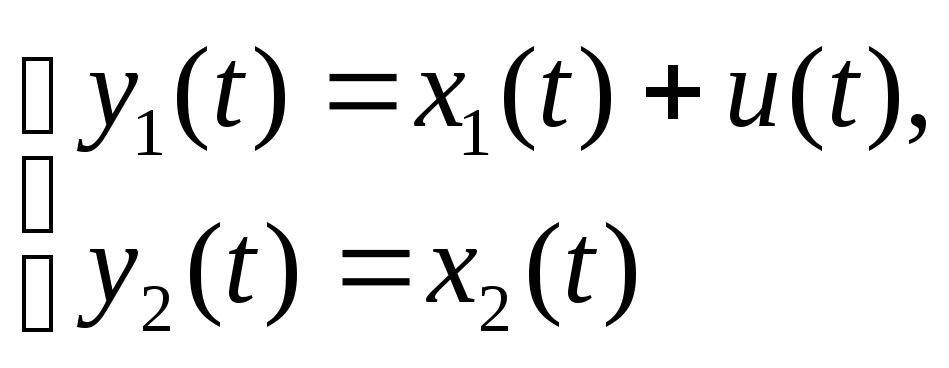описывающую поведение некоторого динамического объекта с одним входом и двумя выходамиВводя соответствующие обозначения и используя матричную запись, можно убедиться, что система описывается четверкой числовых матриц:

, ,

, .

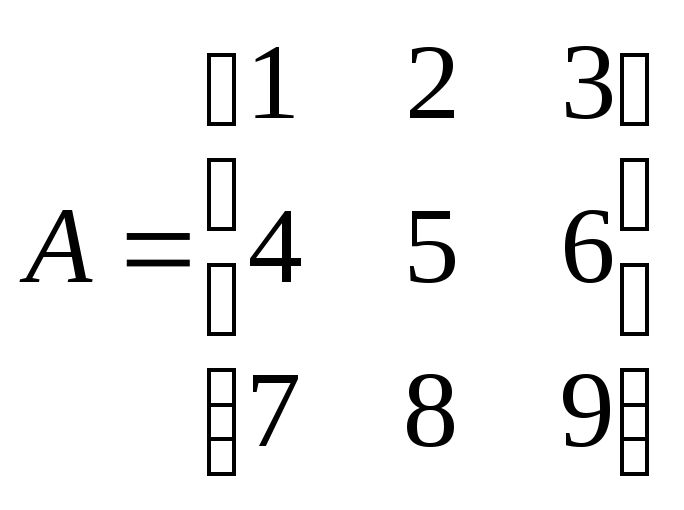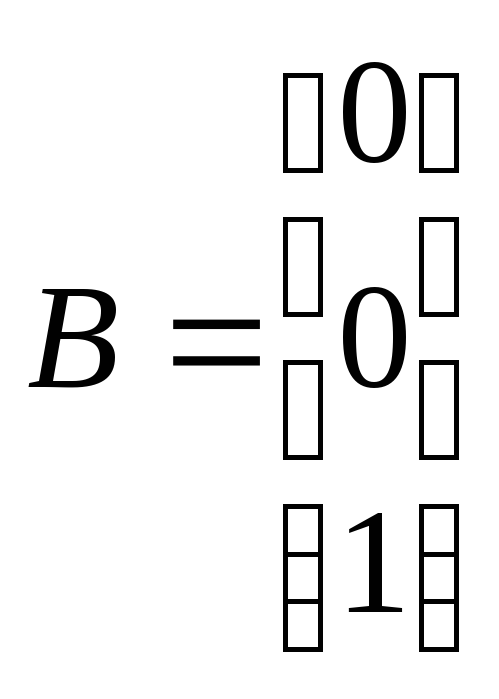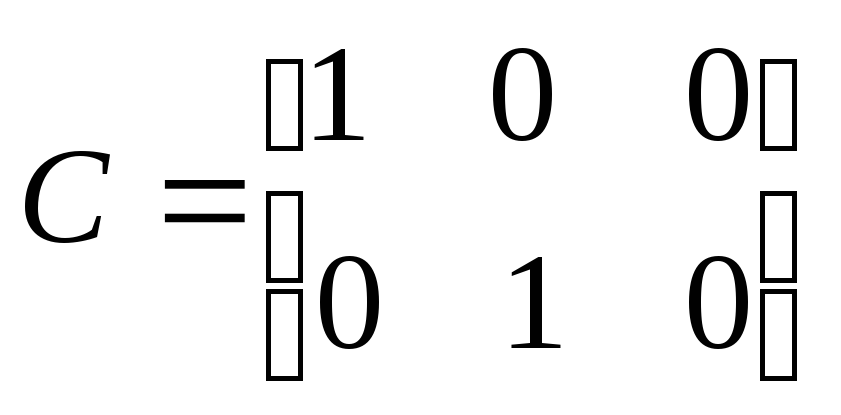Передаточные функции (матрицы) в пространстве состояний

Определим передаточные функции в терминах пространства состояний.

Проведем некоторые формальные преобразования уравнений в пространстве состояний. Как и в случае описания систем в терминах «вход-выход» расмотрим оператор дифференцирования по времени

.

Будем относиться к как к комплексной переменной и рассматривать различные функции от нее. Таким функциям впоследствии придадим содержательный смысл. Например, если

,

то .

Тогда, подставив в (10) (при) и формально разрешая первое из уравнений (10) относительно, получаем выражение

.

Тогда для выхода получаем выражение

.

Определение. Матричная функция комплексной переменной

(15)

называется передаточной функцией от управления к выходу, а аналогичная функция

(16)

называется передаточной функцией от возмущения к выходу. Рассмотрим эти функции подробнее.

Утверждение. Элементами матриц иявляются дробно-рациональные функции от переменной, которые имеют общий знаменатель

. (17)

Справедливость последнего утверждения следует из правила Фробениуса об обращении матриц. Полином называетсяхарактеристическим полиномом системы, т.к. в дальнейшем будет показано, что от значения его корней зависят такие важные свойства системы, как устойчивость и др.

С учетом (17) выражения для и, аналогично,можно представить в виде

и,

где ипредставляют собой матрицы, элементы которых являются полиномами от.

Определение. Нули (т.е. значения корней) характеристического полиноманазываютсяполюсами передаточных функций :

.

Таким образом, полюса совпадают с собственными числами матрицы которые, как известно из соответствующего определения, являются корнями ее характеристического полинома.

Т.е. полюса передаточной функции – это множество точек, где она не определена.

Возвратимся к выражению для выхода системы .

На языке передаточных функций выход системы как функцию от управления и внешних входов можно записать в следующем виде:

(18)

Строгое обоснование перехода от записи (9) системы в пространстве состояний к форме (18) в терминах передаточных функций может быть сделано с помощью преобразования Лапласа. Опуская это обоснование, будем рассматривать (18) просто как другую форму записи дифференциальных уравнений (9).

Представление системы в форме передаточных функций может быть и исходным. Иногда оно возникает более естественно, чем описание в пространстве состояний. Как в этом случае можно перейти к описанию системы в пространстве состояний?

Рассмотрим для простоты ситуацию, когда наблюдаемые внешние возмущения и ошибки измерения выхода (помехи) отсутствуют:

. (19)

В этой записи под передаточной функцией будем понимать матрицу, элементы которой есть дробно-рациональные функции от, т.е. функцияпредставима в виде

,

где элементы матрицыявляются полиномами от. Полином- общий знаменатель элементов матрицы- будем называть характеристическим полиномом системы, а его корни – полюсами передаточной функции (системы). Такое определение характеристического полинома и полюсов системы не вполне точно, поскольку могут возникнуть неприятности, например, с сокращением неустойчивых полюсов (это будет рассмотрено позже).

Более строгое определение дается следующим образом. Формально умножив обе части (19) на , получим

. (20)

Рассматривая теперь как оператор дифференцирования, приходим теперь к системе дифференциальных уравнений высокого порядка относительно. На элементыестественно накладывать дополнительное условие реализуемости: степень полинома в числителе не превосходит степени полинома в знаменателе. Такие передаточные функции называют реализуемыми, или правильными. Тогда, вводя «искусственные» переменные – состояния, можно привести (20) к виду, аналогичному (9).

Иными словами, от записи системы с помощью реализуемой передаточной функции можно перейти к эквивалентному описанию в пространстве состояний. Такой переход принято называть реализацией передаточной функции в пространстве состояний. При этом используют запись

или что означает, что системаэквивалентна системе

и при этом .

Переход от к-реализации может быть осуществлен разными способами, и таких реализаций много. Среди них существуют такие , в которых размерность матрицы, т.е. размерность вектора состоянийминимальна. Их называютминимальными реализациями.

Вообще говоря, для широкогоряда практических задач запись систем с помощью передаточных функций очень удобна. Продемонстрируем это на простом примере. Пусть имеется несколько объектов соответствующих размерностей, соединенных последовательно, так что выход каждого служит входомследующего, причем каждый объект имеет свою передаточную функцию:

.

Мы для простоты полагаем, что имеется единственный входной сигнал , а ошибки измерения (помехи) отсутствуют.

Подставляя последовательно, получаем для связи общего входа и выхода:

,

т.е. передаточная функция последовательного соединения равна произведению передаточных функций объектов:

.

На языке пространства состояний описать такое соотношение было бы значительно менее удобно. Поэтому в инженерной практике, где нередко рассматриваются сложные соединения более простых звеньев (так называемые блок-схемы систем), язык передаточных функций бывает порой предпочтительней, чем описание в пространстве состояний или в терминах «вход-выход». Существуют определенные правила, рассчета передаточной функции блок-схемы всей системы по передаточным функциям ее отдельных звеньев (блоков).

Представим еще одно важное свойство, демонстрирующее удобство такого описания систем.

Пусть система имеет вид:

а входное воздействие представляет собой комплексныйгармонический сигнал

,

где - некоторый постоянный вектор,- частота колебаний (в теории управления мнимую единицу принято обозначать).

Из формулы (11) для решения системы получим:

. (21)

Предположим, что матрица устойчива (об условиях устойчивости матриц и систем будет рассмотрено позднее). Можно показать, что для устойчивых матрицпри.

Черезобозначимустановившееся значение вектора состояния:

. (22)

Тогда можно показать, что из (21), (22) следует, что при.

Таким образом, для установившегося значения выхода имеем:

при .

Или, иначе говоря,

(23)

где матрица называетсячастотной характеристикой системы.

Поясним смысл полученного соотношения (23). Пусть все компоненты входного вектора равны 0 кромей, которую представим в виде:

,

где -й элемент матрицы, а. В силу линейностиотклик системы на сумму вещественной и мнимой составляющихравен сумме откликов на каждую из них, т.е.

если в качестве входа взять вещественную гармонику , то на-м выходе установившееся значение будет

(24)

Отчюда вытекает следующий важный результат: если на й вход системы с устойчивой характеристикой поступает гармонический сигнал с частотой, то на-м выходе получается гармонический сигнал с той же частотой, но амплитуда отличается враз. Эту величину называюткоэффициентом усиления входного гармонического сигнала, в то время как фаза изменяется на .

Передаточные функции дискретных систем

Введем теперь определение передаточной функции для дискретных систем. Определим оператор сдвига назад :

(25)

и аналогично предыдущему случаю будем рассматривать его как формальную переменную. Тогда при первое из уравнений (12):

запишется в виде:

т.е.

Теперь передаточные функции выражаются через переменную по формуле:

, (26)

.

Аналогично непрерывному случаю, будем называть характеристическим полиномом дискретной линейной системы общий знаменатель элементов матричных функций:

от переменной .

Соответственно, как и в непрерывном случае, передаточные функции имеют вид:

,

,

где и - матрицы, элементы которой являются полиномами от .

Поэтому если не имеет нулей внутри единичного круга (т.е. матрица А дискретно устойчива, т.е. для всех собственных значений А), то матричные функции и аналитичны в этом круге.

Аналогично тому, как это сделано для непрерывных систем, можно показать, что если у открытой системы (13): без ошибок наблюдения выхода () матрица А дискретно устойчива, а на вход подается гармонический сигнал

,

то выход системы стремится к установившемуся значению, записываемому формулой:

,

т.е. и в этом случае гармонические сигналы преобразуются в пределе в гармонические с амплитудой, измененной в раз и со сдвигом по фазе, равным . Знак минус соответствует оператору сдвига назад.

Видно, что и в дискретном случае язык передаточных функций хорошо приспособлен к описанию прохождения гармонических сигналов, имеющих фиксированную частоту.

Методы анализа систем, основанные на таком подходе, называют частотными.

Операторный подход к описанию линейных систем в пространстве состояний

Рассмотрим непрерывную стационарную систему:

(27)

при нулевых начальных условиях и отсутствии ошибок на выходе ().

Тогда сигнал на выходе линейно зависит от сигнала на входе:

,

где - некоторый линейный оператор.

Для линейной системы (27) этот оператор является линейным интегральным оператором и имеет явное выражение:

.

Функция называется весовой функцией системы.

Однако можно рассматривать и более общие линейные операторы L, задающие соответствие входа и выхода. При этом система не обязательно приводима к виду (27).

На такие операторы следует наложить естественные ограничения, например, требование причинности: значение выхода в момент не может зависеть от значений входа в будущем .

Кроме того, оператор L должен быть ограниченным в смысле определенной операторной нормы.

Для одномерного случая (когда входной и выходной сигналы скалярные), весовая функция определяется как реакция системы в момент на - функцию:

(функция, имеющая конечное значение при единственном значении переменной (обычно в начале координат) и равная нулю при всех других значениях.), если начальное состояние было нулевое.

Эту функцию называют также импульсной характеристикой системы.

Для одномерных систем в качестве другого «типового» сигнала на входе рассматривают также «единичный скачок», или функцию Хевисайда:

1.

Реакцию системы (при нулевых начальных условиях) на такое входное воздействие называют переходной характеристикой , или переходной функцией. Она связана с импульсной характеристикой соотношением:

.

Способ описания систем с помощью весовой или переходной функций часто применяется при моделировании сложных физических устройств неизвестной структуры.

Управляемые системы. Критерии управляемости