5.5.1. Суммирование случайной и детерминированной функций

Пусть к случайной функции X(t) прибавляется неслучайное слагаемое (х):

Y(t)=X(t)+ (t),

где Y(t)- новая случайная функция.

Посмотрим, как изменяется математическое ожидание и корреляционная функция случайного процесса. Пусть случайная функция X(t) имеет одномерную функцию плотности вероятности f(x,t). Если к случайной величине добавить неслучайную X(t)+ +(t), то закон распределения не изменится. Действительно, (t) означает, что при заданном t - (t) имеет вполне определенное значение. Поэтому при одном и том же t значения X(t) и X(t)+(t) будут иметь одну и ту же вероятность. От прибавления в момент t постоянной величины к X(t) закон распределения только лишь сместится по оси X.

f (y,t)=f[x+),t].

Рассмотрим выражение

Y(t)=X(t)+(t) (5) где Y- случайная величина, X - случайная величина,  - константа (при заданном t).

Найдем дифференциал от левой и правой частей (5): dy=dx (при фиксированном t).

Умножаем (5) на f(y,t)dy и интегрируем:

Так как пределы интегрирования , то

Отсюда следует: m_y=m_x+(t).

Итак, при прибавлении к случайной функции неслучайного слагаемого к ее математическому ожиданию прибавляется то же неслучайное слагаемое.

Корреляционную функцию случайной функции у(t) можно определить следующим образом:

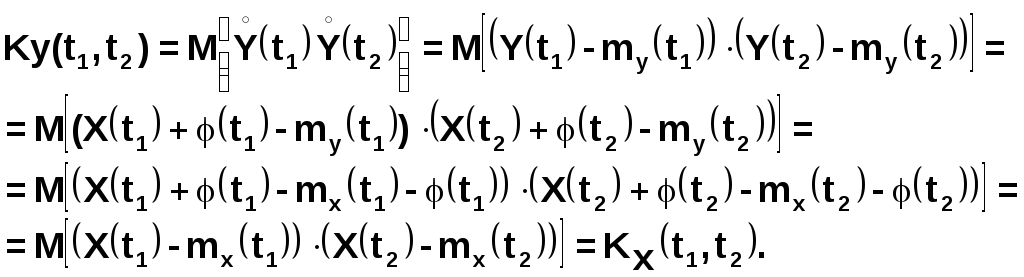
Таким образом, при прибавлении неслучайного слагаемого к случайной функции корреляционная функция случайной функции не меняется.

5.5.2. Интегрирование случайной функции

Пусть

Запишем интеграл как предел суммы:

Применим к последнему выражению операцию математического ожидания:

Математическое ожидание интеграла от случайной функции равно интегралу от ее математического ожидания.

Определим корреляционную функцию Ky(t₁,t₂). По определению корреляционной функции

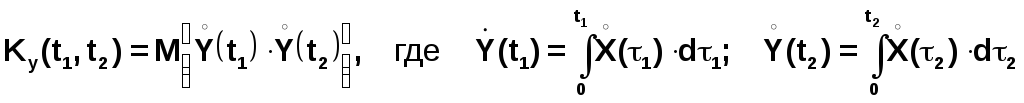
Перемножив последние выражения, получим:

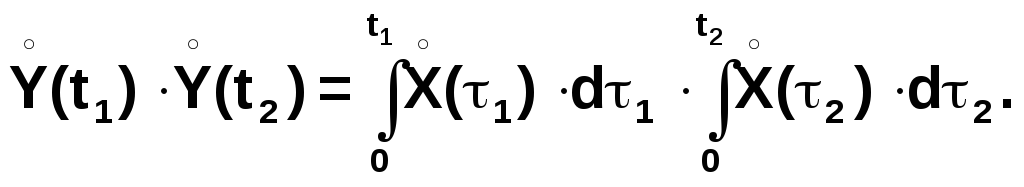
Последнее выражение можно переписать в виде двойного интеграла:

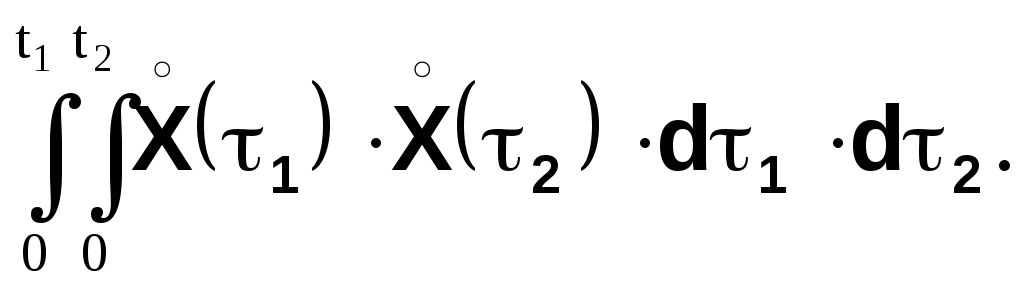
Применив операцию математического ожидания и меняя ее в правой части с операцией интегрирования, получим:

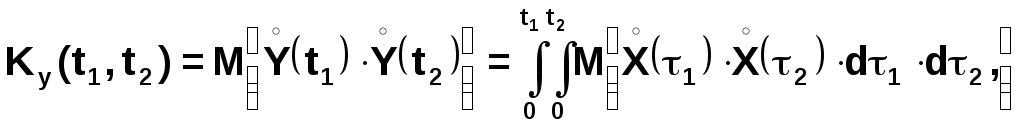что дает окончательно

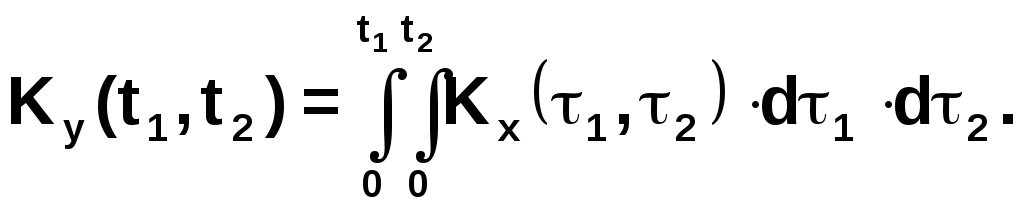
Следовательно, чтобы получить корреляционную функцию интеграла от случайной функции, необходимо дважды проинтегрировать корреляционную функцию исходной случайной функции - первый раз по одному аргументу, затем по другому.

5.5.3. Дифференцирование случайной функции

Пусть

Найдем характеристики случайной функции Y(t): m_y(t) и K_y(t₁,t₂).

Запишем Y(t) как предел отношения

Применяя операцию математического ожидания, получим:

Таким образом, математическое ожидание производной от случайной функции равно производной от ее математического ожидания.

Будем искать корреляционную функцию K_y(t₁,t₂).

По определению

Подставим выражения для

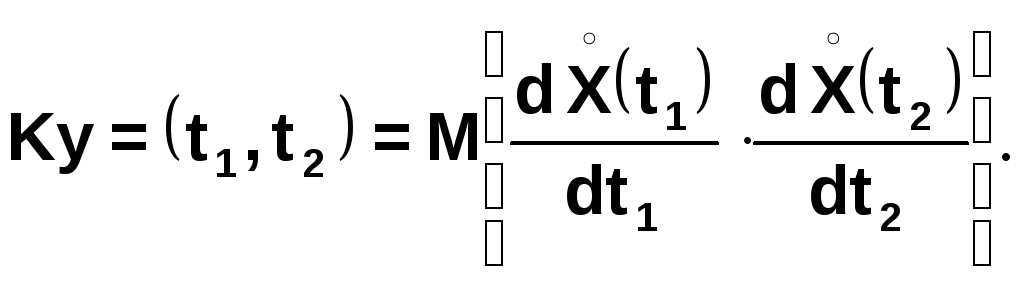
Выражение в квадратных скобках представим в виде второй смешанной частной производной:

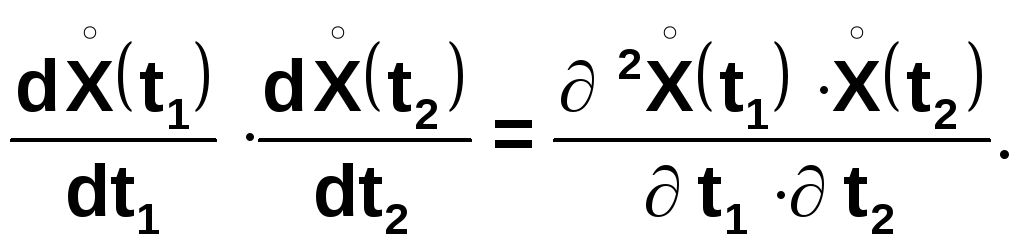
Так как математическое ожидание производной равно производной математического ожидания, получим:

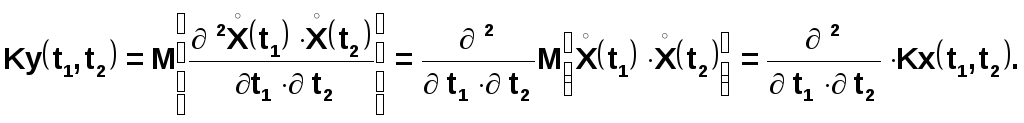
Следовательно, чтобы найти корреляционную функцию производной случайного процесса, нужно дважды продифференцировать корреляционную функцию исходной случайной функции: сначала по одному аргументу, затем по другому.