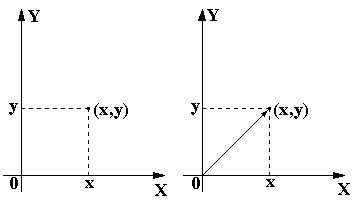5.2. Векторные случайные величины

При совместном изучении нескольких случайных величин их рассматривают как систему случайных величин, либо как случайный вектор, компонентами которого являются отдельные случайные величины. Система двух случайных величин (Х, Y) геометрически интерпретируется как случайный вектор на плоскости X0Y (рис.57), направленный из начала координат в точку (Х, Y) или как случайная точка на плоскости X0Y с координатами (Х, Y). Система трех случайных величин может рассматриваться как вектор в трехмерном пространстве, система n случайных величин - как вектор в n- мерном пространстве. Далее ограничимся рассмотрением системы двух случайных величин.

Рис.57. Двумерный случайный вектор

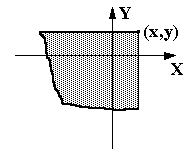
Рис.58. Двумерная функция распределения - вероятность попадания случайной точки в заштрихованную область

5.2.1. Функция распределения двумерного случайного вектора

Функция распределения системы двух случайных величин (двумерного случайного вектора)- это вероятность совместного выполнения двух неравенств Х<x и Y<y

F(x,y)=P(X<x, Y<y).

Геометрически - это вероятность попадания случайной точки (X,Y) в бесконечный квадрат с вершиной (x,y), лежащий левее и ниже ее (рис.58). Определим общие свойства функции распределения системы двух случайных величин.

1. Функция распределения F(x,y) является неубывающей функцией двух аргументов, т.е.

F(x₂,y)F(x₁,y) при х₂>x₁;

F(x,y₂)F(x,y₁) при y₂>y₁.

2. Повсюду на - функция распределения равна нулю:

F(x,- )=F(- ,y)=F(- ,- )=0.

3. При одном из аргументов, равном , функция распределения системы превращается в функцию распределения случайной величины, соответствующей другому аргументу:

F(x, )=F₁(х); F( , y)=F₂(y).

4. Если оба аргумента равны , функция распределения системы равна единице:

F( , )=1.

Для системы двух случайных величин можно поставить задачу о вероятности попадания случайной точки (X,Y) в некоторую область на плоскости X0Y. Чтобы упростить задачу, будем рассматривать область в виде прямоугольника: (рис.59):

Р(х₁X<x₂, y₁Y<y₂) = F(x₂,y₂)-F(x₁,y₂)-F(x₂,y₁)+F(x₁,y₁)

(нижняя и левая границы включены в прямоугольник, а верхняя и правая - не включены).

5.2.2. Функция плотности вероятности двумерного случайного вектора

Рассмотрим систему двух случайных величин Х, Y. На плоскости X0Y выделим прямоугольник со сторонами x и y, примыкающий к точке с координатами (х,y) (рис.60). Вероятность попадания в этот прямоугольник равна:

P[xX<(x+x), yY<(y+y)] = F(x+x, y+y)-F(x+x,y)-F(x,y+y)+F(x,y).

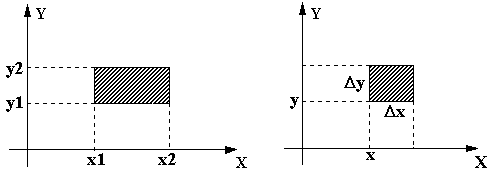
Рис.59 Рис.60

Разделим эту вероятность на площадь прямоугольника и перейдем к пределу при x0 и y0;

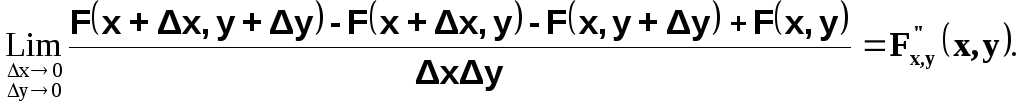
Если F(x,y) непрерывна и дифференцируема, то правая часть представляет собой вторую смешанную частную производную функции F(x,y) по x и по y:

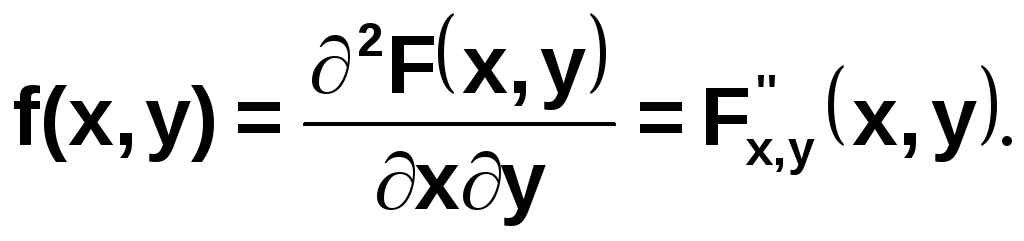
Функция f(x,y) называется плотностью распределения (плотностью вероятности) системы случайных величин.

Для системы случайных величин элемент вероятности f(x,y) dxdy- вероятность попадания случайной точки в элементарный прямоугольник со сторонами dx, dy, примыкающий к точке (x,y). Эта вероятность равна объему элементарного параллелепипеда, ограниченного сверху поверхностью f(x,y) и опирающегося на элементарный прямоугольник dxdy. Вероятность попадания случайной точки в произвольную область D равна интегралу элементов вероятности по всей области D.

Вероятность попадания случайной точки в прямоугольник, ограниченный абсциссами Х₁, Х₂ и ординатами Y₁, Y₂ равна

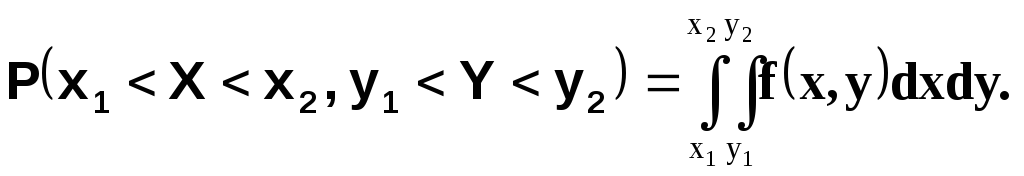
Рассмотрим основные свойства плотности вероятности.

1. Плотность вероятности системы случайных величин - функция неотрицательная

f(x,y)0.

Это ясно из того, что плотность вероятности есть предел отношения двух неотрицательных величин: вероятности попадания в прямоугольник и площади прямоугольника.

2. Двойной интеграл в бесконечных пределах от плотности вероятности системы двух случайных величин равен единице:

3. Одномерные плотности вероятности по двумерной плотности можно определить с помощью следующих формул:

Зависимые и независимые случайные величины. При изучении системы случайных величин часто возникает необходимость выяснить характер взаимной зависимости этих величин.

Случайная величина Y называется независимой от случайной величины X, если закон распределения величины Y не зависит от того, какое значение приняла случайная величина Х. Зависимость величин всегда взаимная. Если величина Y не зависит от Х, то и величина Х не зависит от Y. Зависимость между случайными величинами можно охарактеризовать с помощью условных законов распределения.

Условным законом распределения величины Y, входящей в систему XY называется ее закон распределения при условии, что другая величина X приняла определенное значение. Условный закон распределения можно задавать как функцией распределения, так и плотностью вероятности. Условная функция распределения случайной величины y обозначается F(y/x). Условная плотность вероятности - f(y/x).

Для независимых случайных величин f(x,y)=f(x)f(y).