Пусть в системе, представленной линейной моделью в пространстве состояний

(см. (9)),

где - начальное условие,

управление является программным, т.е. задается в виде функции времени: .

Уточним, в каком классе ищутся функции , т.е. какие на них накладываются дополнительные ограничения. Эти функции могут, в частности, быть гладкими, непрерывными, либо произвольными функциями времени. Последнее означает, что в принципе допустимы разрывные управления.

Как правило, в практических задачах на функции управления накладываются условия ограниченности. Типичным для широкого класса задач является условие ограниченности типа:

для всех ,

где - заданное замкнутое ограниченное множество в.

Другой тип ограничений на управления – интегральные, например:

,

где - заданная длительность процесса управления.

После выбора программного управления, т.е. вида функции , можно сделать соответствующую подстановку в выражение (9) и получить систему обыкновенных дифференциальных уравнений, в которых фигурируют только внешние воздействия. Например, уравнение состояния приобретает вид:

и если известны, томожет быть рассчитано по формуле:

для всех значений . Подчеркнем, что для этого требуется знание всех указанных выше величин.

Разумеется, программное управление может применяться и в дискретных системах (выбирается заранее как функция от), никаких особенностей по сравнению с непрерывным случаем нет.

Используем программное управление для анализа понятия управляемости системы.

Напомним определение управляемой системы.

Система

,

называется управляемой, если для любого конечного инайдется такое непрерывное либо кусочно-непрерывное управлениена интервале, что решение системы принимает нулевое значение в момент.

Другими словами, в управляемой системе начальное отклонение может быть устранено за (любое) конечное время.

Очевидно, что, поменяв направление времени, мы получим, что управляемая система переходит из в любое заданное.

Иногда приводят более общее определение: система управляема, если для любых

и любого найдется управление, переводящее систему из состоянияв состояние. Некоторые авторы называют такие системывполне управляемыми, но мы будем придерживаться более общей терминологии.

На практике нередко возникают ситуации, когда количество управляющих воздействий (размерность пространства управлений) меньше количества управляемых величин (т.е. меньше размерностивекторов состояний). Однако такого типа трудность при решении задачи можно преодолеть следующим образом.

Определение. Пара матриц называется невырожденной (управляемой) парой, если ранг матрицы

(28)

равен . Матрицаназывается матрицей управляемости.

Некоторые определения и свойства из теории матриц и линейных пространств

1. Степень матрицы.

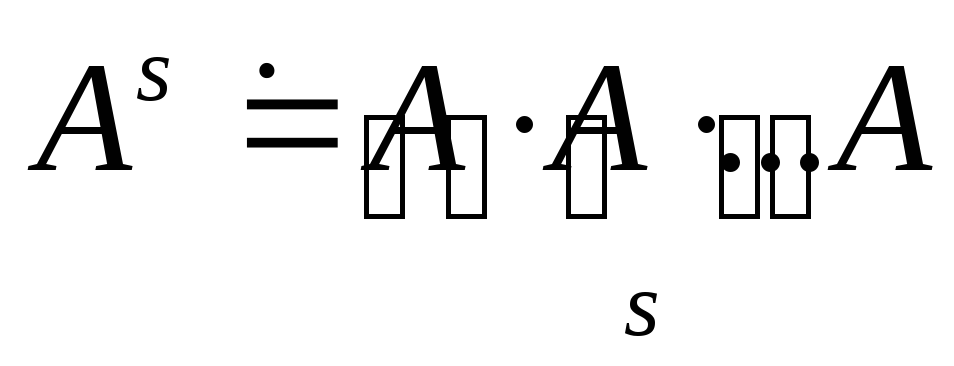
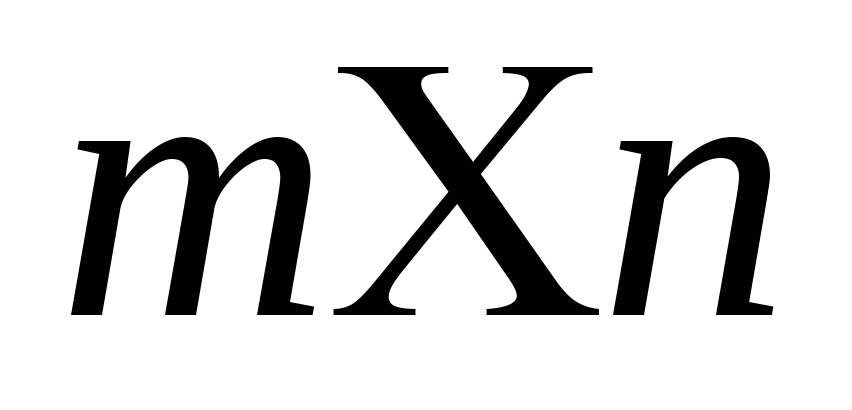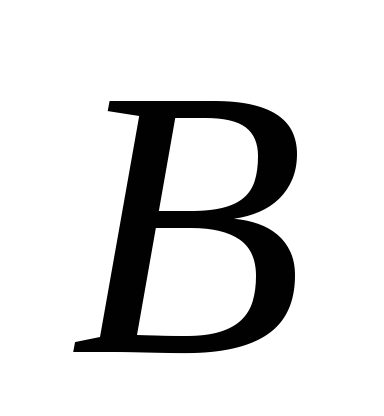2. Произведением матриц размерностииразмерности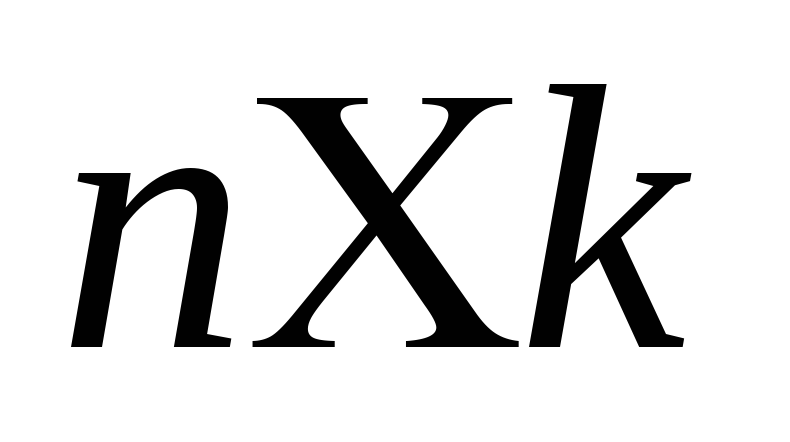называется матрица С размерности, такая, что каждый ее элемент на пересечении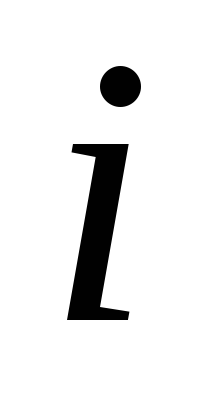-й строки и-го столбца равен сумме попарно умноженных элементов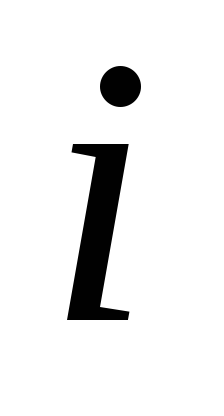-й строки первой матрицы на элементы-го столбца второй матрицы, т.е.

.

Произведение матрицы-строки на матрицу столбец дает скаляр, произведение матрицы-столбца на матрицу-строку дает прямоугольную матрицу.

Особенность: произведение матриц, вообще говоря, не коммутативно, т.е. в общем случае .

3. Диагональная матрица

представляет собой квадратную матрицу размерности вида:

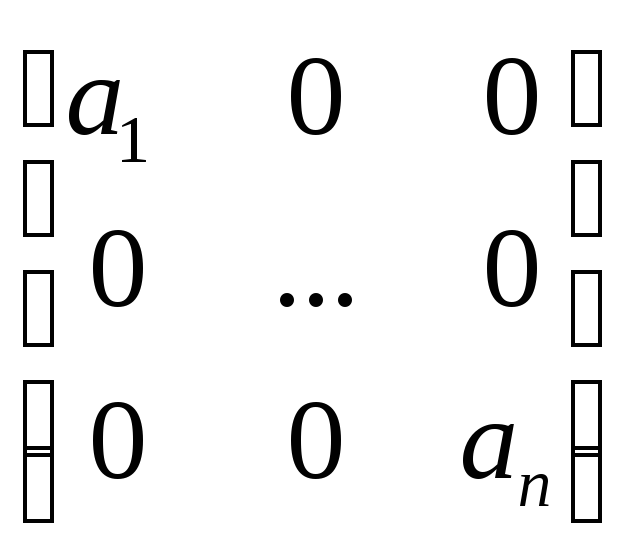, местоположение ненулевых компонентов в этой записи называется главной диагональю матрицы.

4. Единичная матрица – это диагональная матрица, у которой на главной диагонали все элементы равны единице:

.

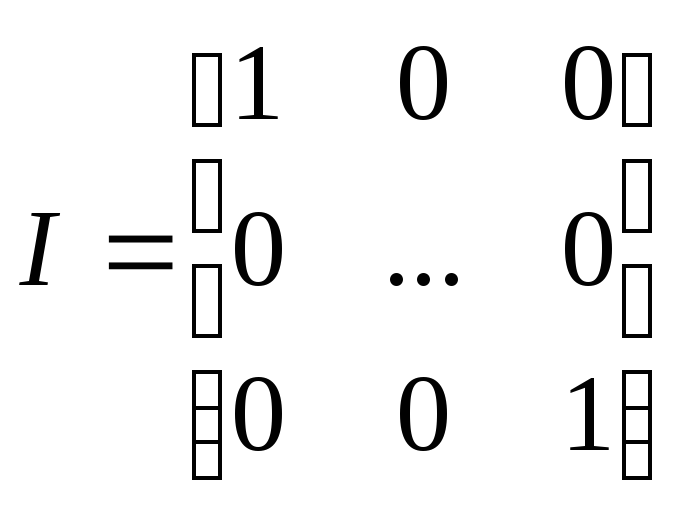5. Транспонирование матриц. Для любой матрицы размерности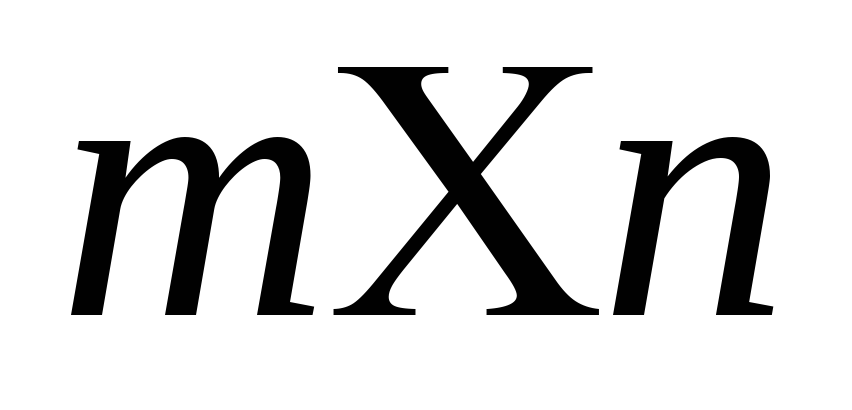существует так называемая транспонированнаяматрица размерности, так что между элементами матриц существует отношение вида:

. В частности, для матрицы-строки транспонированная матрица – это матрица-столбец с тем же количеством элементов, а для матрицы-столбца транспонированная матрица – это матрица-строка.

6. Матрица называетсясимметрической, если .

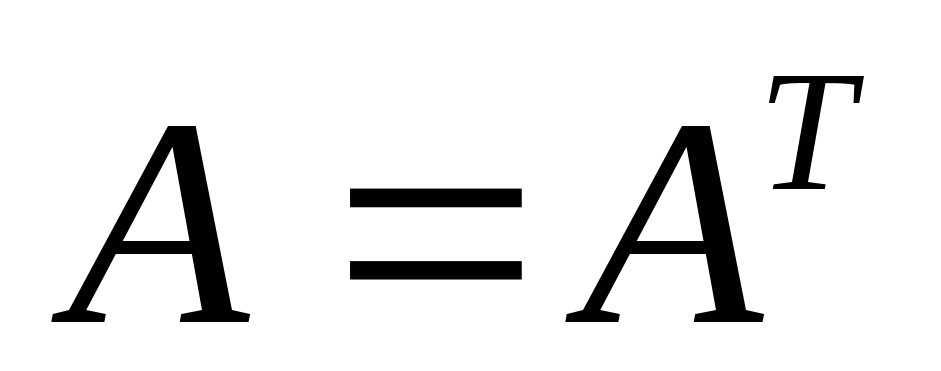7. Если имеет место тождество

, где - единичная матрица, то матрицаназываетсяортогональной.

8. Понятие определителя матрицы вводится для квадратных числовых и полиномиальных матриц. С геометрической точки зрения для матрицы размерности 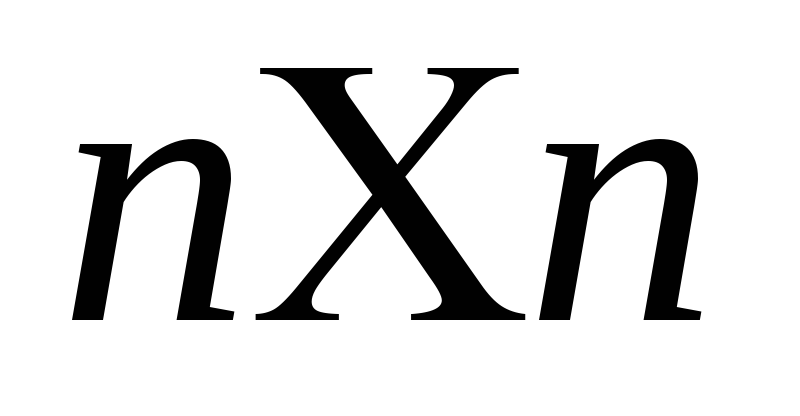определитель представляет собой скалярную величину, характеризующую в -мерном пространстве объем параллелепипеда, ребра которого совпадают со строками или столбцами этой матрицы.Для обозначения определителя используются символы:

.

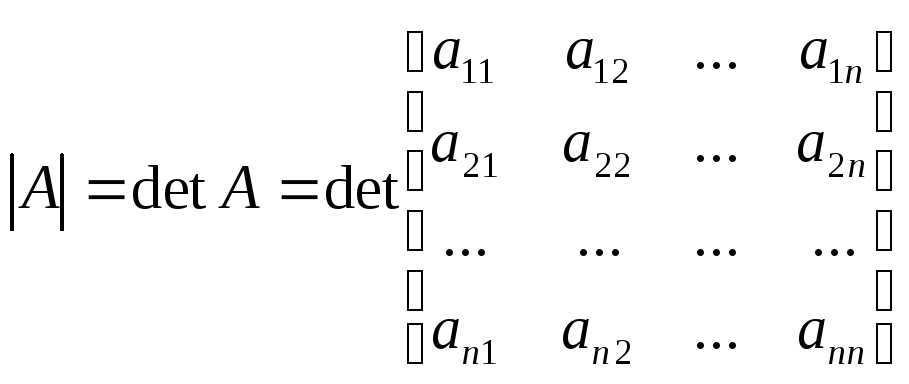Одним из наиболее распространенных способов вычисления определителей является так называемое разложение Безу (некоторые авторы называют его разложением Лапласа). Оно дает следующую формулу для вычисления определителя квадратной матрицы:

,

где - так называемое алгебраическое дополнение для элемента, которое вычисляется по формуле:

.

Здесь в квадратных скобках приведена матрица, которая получается из матрицы вычеркиванием-й строки и-го столбца. Такая формула предполагает рекурсивное использование, т.е. последовательную подстановку формул друг в друга с уменьшением размерности вплоть до получения скаляров.

9. Для того, чтобы ввести понятие ранга матриц, введем несколько основных определений, связанных с линейной независимостью столбцов и строк матриц. Они (столбцы и строки) представляют собой векторы в пространствах определенной размерности.

Векторы называются линейно зависимыми, если существуют такие числа , одновременно не равные нулю, что линейная комбинация этих векторов равна нулю:

.

Из этого тождества следует, что при условии хотя бы один из векторов можно выразить линейной комбинацией остальных по формуле:

Известна теорема, формулирующая условия линейной зависимости векторов:

• Наличие хотя бы одного нулевого вектора

• Наличие хотя бы одной линейно зависимой подсистемы

• Хотя бы один вектор является линейной комбинацией остальных.

10. В противном случае векторы называются линейно независимыми.

11. Основные утверждения, определяющие линейно независимые системы векторов:

• Система из одного вектора независима, если вектор ненулевой

• Система из двух векторов независима, если они не коллинеарны (не лежат на параллельных прямых и их координаты не пропорциональны)

• Система из трех векторов независима, если они не компланарны (не лежат в параллельных плоскостях, определитель из их координат не равен нулю)

• Любая подсистема линейно независимых векторов линейно независима

• Если к системе линейно независимых векторов добавить еще один вектор и она в результате станет линейно зависимой, то этот дополнительный вектор можно представить как линейную комбинацию векторов исходной системы

12. Максимальное количество линейно независимых векторов из какого-то множества (пространства) называется размерностью векторного пространства.

13. Конечная упорядоченная совокупность любых линейно независимых векторо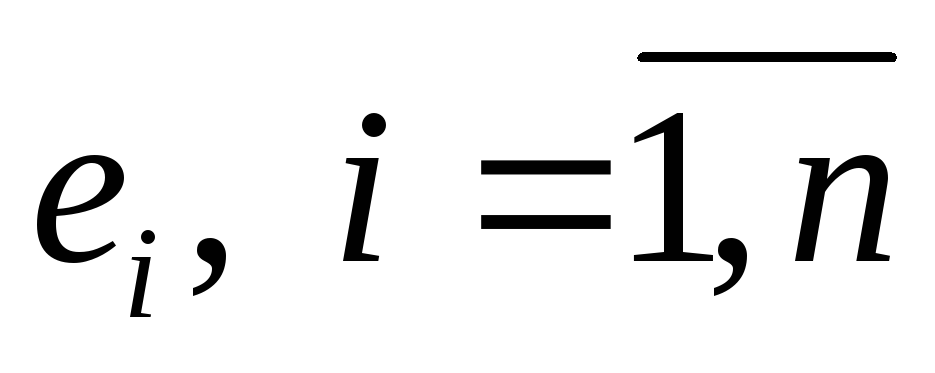в в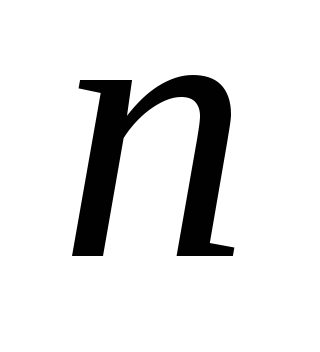-мерном пространстве называется егобазисом.

14. Любой вектор из данного пространства можно представить как линейную комбинацию векторов базиса:

.

Числа называются компонентами, иликоординатами вектора в выбранном базисе (в выбранной системе координат)

12. Если рассматривать не все векторное пространство, а некоторое подмножество (совокупность) векторов, то число векторов базиса называют рангом () системы векторов.

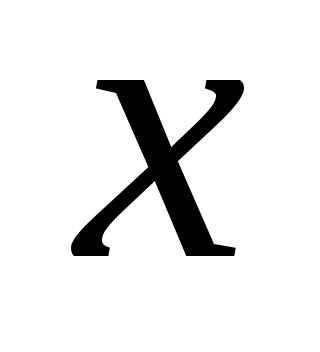13. Два вектора иодинаковой размерности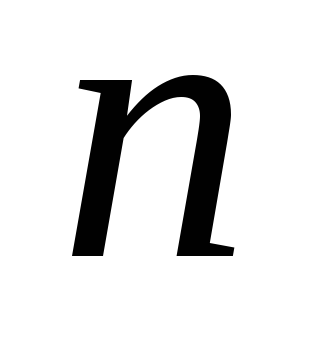называютсяортогональными, если равно нулю их скалярное произведение:

12. Множество векторов 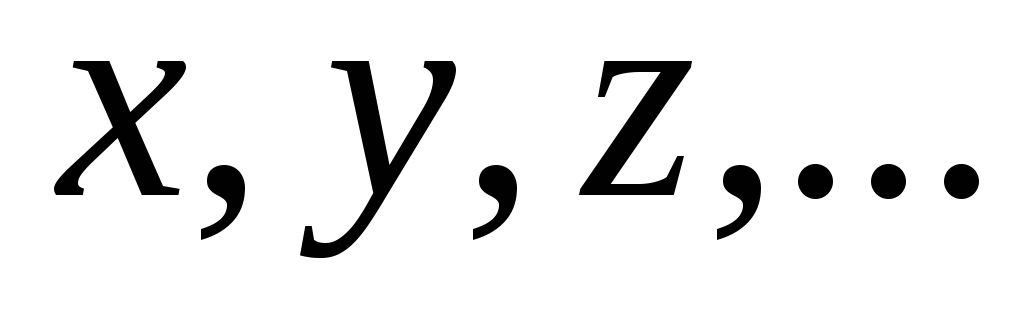называется ортогональным, если любая пара векторов из этого множества ортогональна.

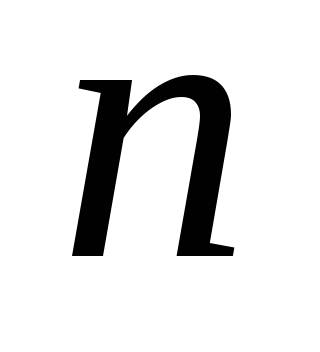13. Если матрица представляет собой форму записи линейного оператора, переводящего векторразмерностив другое линейной пространство:

, то существенно различаются случаи, когда эта матрица является квадратной и невырожденной (ее определитель отличен от нуля), вырожденной, и случай прямоугольной матрицы.

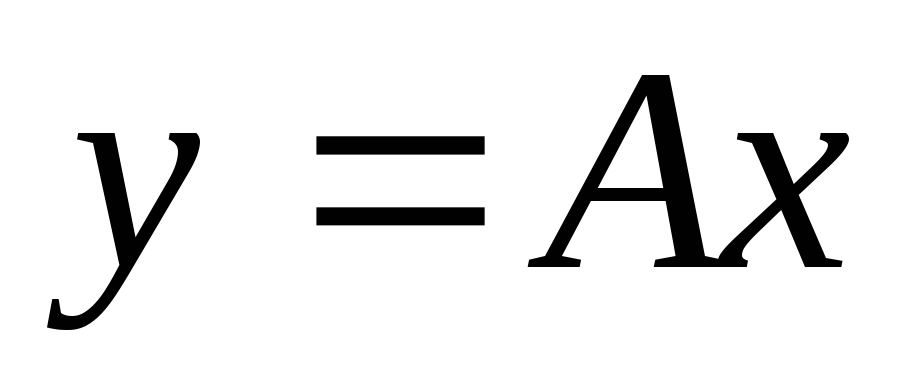12. Если матрица квадратная и невырожденная, то преобразованиеявляетсяэквивалентным и существует обратное преобразование .

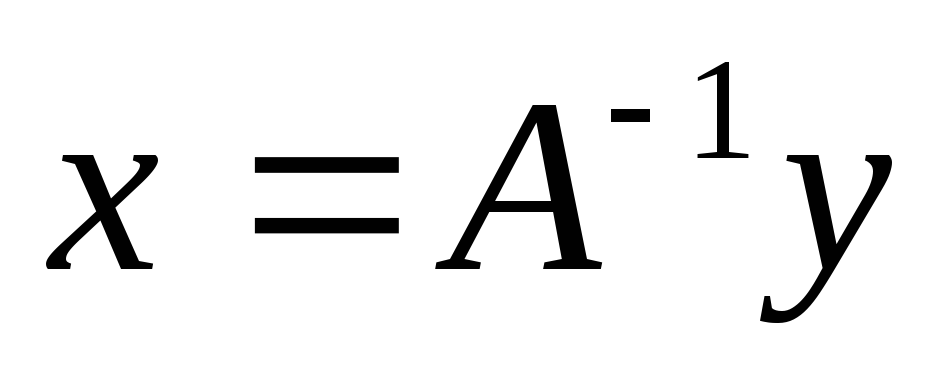К эквивалентным преобразованиям, например, относится замена системы координат.

12. Если матрица - прямоугольная:

,

то каждый из столбцов этой матрицы можно рассматривать как векторнекоторого-мерного пространства, а каждую изстрок – как векториз другого --мерного пространства. Тогда для каждого из этих множеств можно использовать понятие ранга системы векторов, приведенное выше.

21. Можно доказать, что столбцовый ранг матрицы равен ее строчечному рангу и равен максимальному числу линейно независимых векторов.

22. Ранг матрицы не меняется при всех элементарных преобразованиях (умножение строки или столбца на число, перестановка строк или столбцов), а также при транспонировании матриц.

Вычисление ранга матрицы может быть осуществлено разными способами. Один из них основан на том, что с помощью элементарных преобразований можно сделать равными нулю все линейно зависимые строки (столбцы), а линейно независимые строки (столбцы) можно привести к ступенчатому виду. Тогда число ненулевых строк (столбцов), составляющих невырожденный блок матрицы, равно ее рангу.

Вернемся к определению управляемости линейной системы. Матрица

составлена из блоков, каждый из которых – матрица размерности, т.е. в целомпредставляет собой матрицу размерности. Например, если(система с одним входом),, то- матрица размерности, столбцы которой являются векторами.

Существует утверждение, что в этом случае пара управляема, если эти векторы линейно независимы.

Следующая теорема дает конструктивные необходимые и достаточные условия управляемости линейных систем.

Теорема. Система

где - начальное условие,

управляема тогда и только тогда, когда .

Доказательство. Необходимость. От противного: пусть . Тогда найдется вектор, такой, что.

По теореме Кэли-Гамильтона матрица удовлетворяет своему характеристическому уравнению: если, то

.

Отсюда следует

.

Умножая последнее равенство на ,, получим, чтои для всех

Но тогда .

С другой стороны, решение системы при программном управлении имеет вид

,

поэтому для имеем:

для любого управления . Ясно, что равенствоне может выполняться при произвольных, например, при.

Доказательство достаточности. Укажем конкретный вид управления, которое переводит систему из в. Например, выберем

где вектор должен выбираться из условияи,

т.е. .

Покажем, что в этом случае матрица

не вырождена. Она называется грамианом управляемости. Прежде всего,

для любого , т.е. эта матрица неотрицательно определена. Покажем, что она строго положительно определена.

Если предположить, что это не так, т.е. что для некоторого вектора, то отсюда последует тождестводля всех.

Тогда и все производные этой функции равны нулю.

, ,

т.е. приЭто означает, что противоречит условию. Таким образом,, поэтому уравнениеимеет решение

при любом .

Тем самым мы нашли управление

которое переводит систему из состояния в состояние.

Для произвольных иуправление, переводящее систему из состоянияв состояниеи минимизирующее функционал

,

(который иногда называют функционалом энергии), имеет вид:

в частности, при получаем:

-

уравнение минимальной энергии, переводящее систему из нуля в заданное состояние .

Аналогичные результаты имеют место и для дискретных систем.

Определение упавляемости для дискретных линейных систем

Дискретная система

(29)

называется управляемой, если для любого и некоторогонайдутся такие ограниченные управления, которые переводят систему в начало координат:.

Решением системы (см. лек.2) является:

.

Требование управляемости приобретает форму: для всякого вектора найдетсяи векторы, такие, что

. (30)

Отсюда вытекает критерий управляемости для дискретных систем.

Критерий управляемости для дискретных систем

Теорема.

Система (29) управляема тогда и только тогда, когда ранг матрицы равен.

Действительно, выбрав , перепишем уравнение (30) в виде, где обозначено, и. Это уравнение имеет решение при любомтогда и только тогда, когда ранг матрицыравен.

Заметим, что в отличие от непрерывных систем дискретное время не может выбираться призвольно: требуется определенное количество шагов, чтобы «накопить» ранг матрицы . Если рангбольше единицы, то систему можно привести в начало координат за число, меньшее. В частности, если матрицаневырождена, то мы достигаем цели за один шаг.

Подход с точки зрения программного управления допустим, когда нет внешних возмущений, матрицы известны и задан некий критерий оптимальности типа функционала энергии. Например, в линейно-квадратичной задаче оптимального управления можно найти оптимальное управление.

В более общих случаях – при наличии внешних возмущений, или неопределенности в описании системы – применение программного управления может привести к резкому ухудшению качества процесса и даже к катастрофе. Представим себе процесс управления самолетом, рассчитанный заранее, до начала полета и не предусматривающий использования поступающей информации о скорости ветра, высоте и других параметрах. Вряд ли такое управление допустимо. Это же относится к большинству ситуаций, связанных с управлением производственными процессами, транспортом, системами связи, финансовыми системами и т.п. В связи с этим будут рассмотрены иные подходы к выбору управления.

Синтез управления

Рассмотрим подход к проблеме управления, связанный с идеей обратной связи.

Управление при таком подходе не выбирается заранее, а корректируется в каждый текущий момент на основании информации о состоянии системы.

Выбор управления в виде функции от состояния и момента времени называется синтезом управления:

. (31)

Эта функция, в принципе, может быть нелинейной по . Существуют различные подходы, позволяющие решать задачу оптимального синтеза при некоторых конкретных постановках задачи оптимального управления. Однако после выбора управления в форме (31) уравнение состояния становится нелинейным и нестационарным. Ограничимся далее случаем линейной статической обратной связи по состоянию:

, (32)

где матрица усиленияне зависит от.

Оказывается, во многих задачах управления такого типа обеспечивают наилучшее значение критерия оптимальности в классе любых управлений, т.е. переход к нелинейным нестационарным обратным связям не улучшает критерия качества.

Подставим управление (32) в выражение для системы (9), тогда получим выражение для замкнутой системы:

,

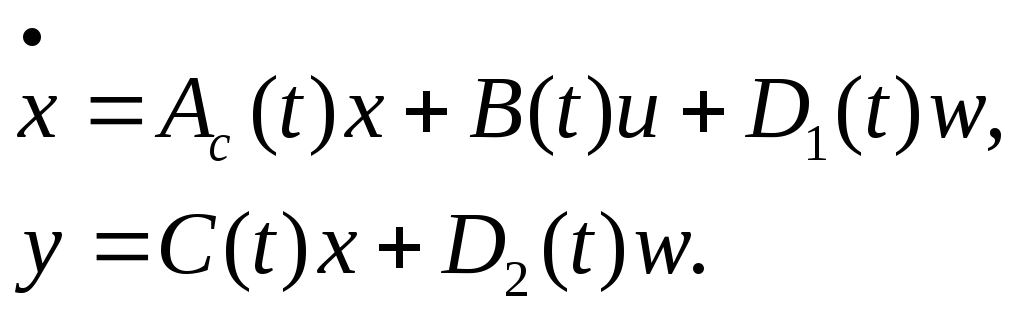
Таким образом, после замыкания системы обратной связью вида (32), мы опять получаем уравнение состояния, но уже с измененной матрицей состояния . В дальнейшем покажем, что за счет выбора матрицы усиленияможно улучшить свойства системы, например, сделать матрицу устойчивой, тогда кактаковой не является.

Управления типа (32) называются линейными регуляторами. Большинство регуляторов, используемых на практике, является линейными. Они легко реализуются технически.

В то же время отметим, что возможности линейных регуляторов в некоторых отношениях ограничены. Так, линейный регулятор в системе без возмущений не может устранить начальное отклонение за конечное время, т.е. не может перевести систему из состоянияв начало координат за конечное время даже при выполнении условия управляемости. Действительно, из уравнения замкнутой системыи условияследует, что. Поэтому управление, которое выбиралось при доказательстве теоремы о критерии управляемости, не было стационарной обратной связью.

В дискретных линейных системах обратная связь имеет вид:

,

и уравнения замкнутой системы приобретают вид:

.

Таким образом, матрица состояний замкнутой дискретной системы пересчитывается по той же формуле, что и в непрерывном случае.

Наблюдаемость. Критерий наблюдаемости

Понятие наблюдаемости тесно связано с понятием управляемости. Управляемость означает, что, зная начальное состояние и матрицы, характеризующие рассматриваемую систему, можно найти вход, который переводит это состояние в нулевое конечное время. Наблюдаемость означает, что знания матриц, характеризующих систему, и реакции при нулевом входе Y[0,t] на конечном интервале достаточно для однозначного определения начального состояния данной системы.

Определение. Система, описываемая (1) и (2) называется наблюдаемой в том случае, когда, для некоторого Т>0 и всех возможных начальных состояний х(0), значения матриц А и С и реакции при нулевом входе Y[0,t] достаточно, чтобы определить начальное состояние x(0).

Теорема. Критерий наблюдаемости. Система, Y описываемая (1), (2), наблюдаема в том и лишь в том, случае, если на np столбцов матрицы Р=[С* ,А* С* ,..,А*^(n-1) С* ] натянуто пространство состояний ℇ . ( Матрицы А*, С*,. получаются транспонированием матриц А, С,. и заменой их элементов комплексно сопряженными.)