метод. НГ краткий курс. 2010

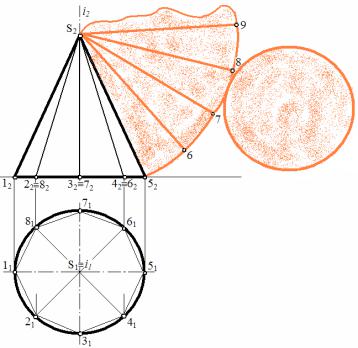
натуральную величину. Поэтому можно построить развертку конуса без дополнительных преобразований.

Рис.101

2. Развертка наклонного (эллиптического ) конуса

Задача. Построить развертку наклонного конуса. Нанести на развертку линию пересечения конуса фронтально проецирующей плоскостью ∑ (рис. 102).

Решение:

Как говорилось выше, развертки наклонных поверхностей строятся приближенно. Боковая поверхность конуса аппроксимируется вписанной в нее многогранной поверхностью пирамиды, которая и развертывается. Натуральные величины боковых ребер (образующих конуса) вписанной пирамиды определяются способом вращения вокруг горизонтально проецирующей оси i.

Развертка построена по точкам засечками из точки S2 (вершины конуса) радиусом, равным длине образующей, и отрезком m, равным стороне основания вписанной 8-гранной пирамиды. Поскольку развертку начали строить со 2-ой образующей, то и закончили ее построение так же этой образующей.

Перенесли точки пересечения конуса фронтально проецирующей плоскостью ∑, определив предварительно данные точки на натуральных величинах каждой образующей.

71

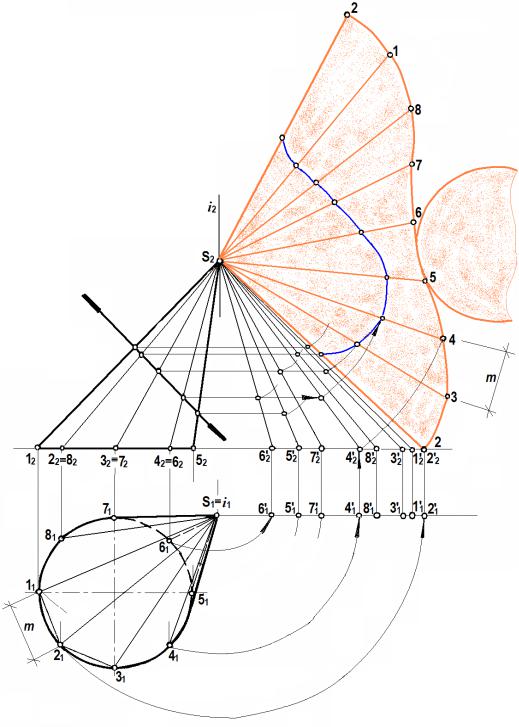
Рис. 102

3. Развертка прямого кругового цилиндра

Задача. Построить развертку прямого кругового цилиндра

(рис.103).

Решение:

Как и в рассмотренной выше задаче, в поверхность цилиндра вписывается n-гранная призма. Нет необходимости определять натуральные величины образующих и основания цилиндра, т.к. они уже спроецированы в натуральную величину. Поэтому сразу строится развертка поверхности.

72

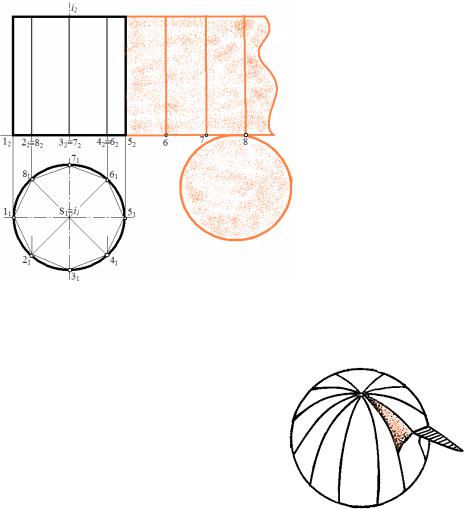
Рис.103

4. Развертка поверхностей сферы и тора

Поверхность сферы и тора развертываются приближенно.

Суть построения состоит в том, что развертку поверхности строят, разделив ее на равные доли (рис. 104) по меридианам, и каждую часть как бы «снимают» с шара. И, таким образом, строя развертку одной доли, другие – ее повторяют.

Рис. 104

Итак, один из способов развертки заключается в аппроксимации сферических элементов сферы цилиндрическими. Для этого поверхность сферы делится меридианами на части. Участки поверхности, заключенные между смежными меридианами, заменяются цилиндрической поверхностью, которая и развертывается.

Задача. Построить развертку полусферы (рис.105). Определить на развертке положение точки К.

Решение:

Разделим поверхность полусферы меридианами на 16 равных частей, которые проецируются на горизонтальную плоскость секторами. Часть сферической поверхности, заключенную между смежными меридианами АО и ВО, заменим цилиндрической поверхностью, касательной к сфере по главному меридиану. Разделим фронтальную проекцию этого элемента на четыре равные части (расстояние m между точками). Определим горизонтальные проекции отрезков очерковых образующих 1,2,3,4 цилиндрического элемента.

Построим развертку этого элемента цилиндрической поверхности. На свободном месте чертежа наметим ось симметрии

73

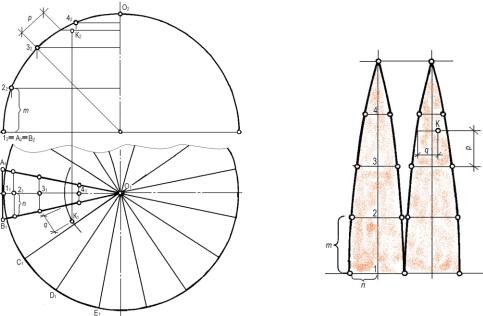
элемента и отложим на ней четыре раза отрезок m – расстояние между делениями главного меридиана (очерковой образующей). В полученных точках откладывают по горизонтали отрезки образующих цилиндрического элемента - n, взятые с горизонтальной проекции.

Положение точки К, принадлежащей сфере, определяют на развертке с помощью двух измерений p и q («координаты» точки), взятых с фронтальной и горизонтальной проекций.

Рис. 105

Раздел 8

8.ПРОЕКЦИИ С ЧИСЛОВЫМИ ОТМЕТКАМИ

8.1.Сущность метода проекций с числовыми отметками

Способы изображения, рассмотренные ранее, оказываются неприемлемыми при проектировании таких инженерных сооружений, как полотно железной или шоссейной дорог, дамбы, аэродромы, различного рода коммуникаций, т.е. в тех случаях, когда высота объекта существенно меньше его размеров на плане. Изображением только плана инженерного сооружения и ограничиваются в методе проекций с числовыми отметками.

К основным достоинствам проекций с числовыми отметками относятся: простота построений, удобоизмеряемость (вертикальные размеры даны в готовом виде, горизонтальные измеряются непосредственно в истинную величину) и относительная простота решения метрических задач. Недостатком является малая наглядность

74

изображения, что в некоторых случаях приводит к необходимости дополнения его вертикальными сечениями (разрезы, профили).

Сущность метода заключается в том, что геометрический образ ортогонально проецируется только на одну горизонтальную плоскость проекций (план), называемую обычно плоскостью нулевого уровня - П0. Проецирование ведется параллельными лучами перпендикулярно данной плоскости.

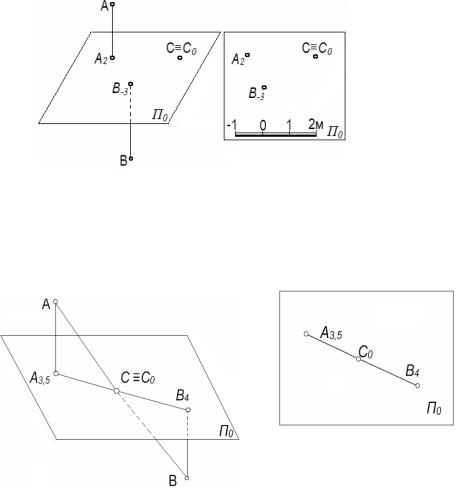
Чтобы по проекциям точек судить о положении этих точек в пространстве, рядом с проекцией каждой точки проставляется цифра – отметка, указывающая расстояние в метрах от точки до плоскости нулевого уровня (рис. 106). Т.е. числовые отметки играют роль фронтальной проекции.

Точки, расположенные над плоскостью нулевого уровня имеют положительные отметки, а точки, расположенные ниже плоскости П0 - отрицательные отметки. Точки, лежащие в плоскости уровня имеют нулевую отметку.

Числовые отметки могут быть мерные (мм, см, м) или заданы линейным масштабом, который представляет собой шкалу из равных отрезков, обозначенных последовательным рядом чисел. Такие отрезки являются масштабными единицами и выражаются в метрах

(м).

Рис. 106

8.2. Изображение прямой

Прямая линия может быть задана проекциями двух любых ее точек. Итак, в пространстве расположена точка А, высота ее 3 единицы (рис. 107).

Рис. 107

75

Проецируем ее на плоскость П0, получаем точку А3. Таким образом, точка А расположена над плоскостью П0 на высоте 3 единицы. Точка В находится под плоскостью П0 , ее проекция - В-4. Соединяем данные точки, получили прямую АВ. Также появилась точка С – точка пересечения прямой АВ с плоскостью П0, ее отметка = 0. Таким образом, точка С0 –это след прямой АВ. Прямая, соединяющая проекции А3 и В4 точек А и В, является проекцией отрезка АВ - прямой линии.

8.3. Прямые частного положения

Горизонтальная прямая (параллельная П0) проецируется на плоскость П0 двумя точками, имеющими одинаковые числовые отметки (рис. 108).

Вертикальная прямая (перпендикулярная П0) проецируется на плоскость П0 в точку, имеющую две отметки.

Рис. 108

8.4.Заложение, превышение, интервал

иуклон прямой

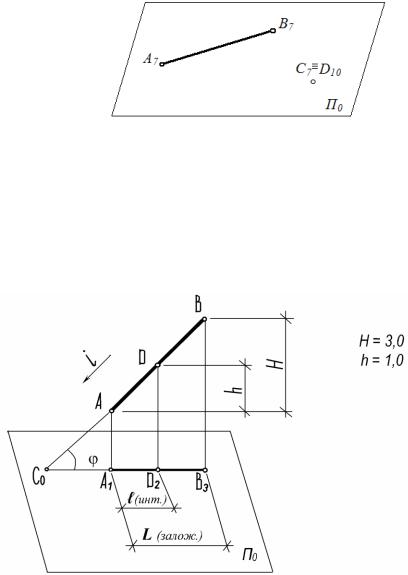
На рис. 109 изображена прямая АВ и ее проекция А1В3 на нулевую плоскость П0.

Рис. 109

76

Длина горизонтальной проекции А1В3 называется заложением отрезка прямой и обозначается символом L.

Разность отметок концов отрезка прямой АВ называется

превышением (подъемом) отрезка и обозначается Н.

Разделив прямую АВ на равные отрезки, получим точку D с

отметкой 2 - D2.

Если разность отметок двух точек прямой равна единице, то заложение отрезка прямой, определяемого этими точками, называется

интервалом прямой и обозначается ℓ.

Иными словами, интервал прямой - это заложение, соответствующее подъему, равному единице.

ℓ=L/Н; (1)

где: L – заложение;

Н– превышение (подъём);

ℓ-интервал заложения, приходящийся на единицу превышения. Уклон прямой определяется тангенсом угла наклона прямой к

плоскости уровня.

i = tg ,

где - угол наклона прямой к плоскости П0.

Уклоном прямой называется отношение превышения прямой к ее заложению.

Из равенства следует, что уклон линии является величиной, обратной ее интервалу.

Уклон и интервал прямой могут быть вычислены при помощи равенств (1) или (2) или определены графически, при помощи совмещения прямой с плоскостью П0 и выполнения построений, рассмотренных выше.

Следствие: прямую линию в проекциях с числовыми отметками можно также задать направлением ее проекции с проекцией одной точки и интервалом или уклоном.

Понятия уклон и интервал используются для характеристики продольного профиля пути, крутизны откосов насыпей и выемок.

8.5. Градуирование прямой

Градуирование прямой – нахождение на проекции прямой точек, имеющих целые числовые отметки.

Градуирование основано на способе пропорционального деления отрезка прямой линии.

77

Задача. Проградуировать прямую АВ, заданную проекцией

А20 В27 .

Решение:

Задачу решают, используя теорему Фалеса (рис. 110).

Рис. 110

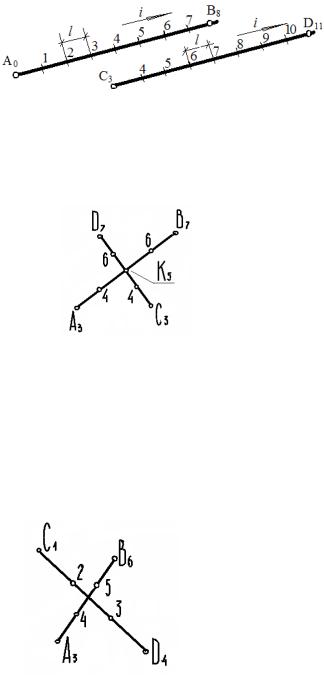
Проводим через точку В в произвольном направлении линию и откладываем на ней через равные промежутки отрезки с 21 до 27. Затем соединяем точку 27 с точкой А27. Параллельно полученному отрезку прямой проводим прямые от точек 21 – 26. Эти прямые пересекут отрезок АВ в определенных точках, которые и делят саму прямую АВ на равные промежутки от 20 до 27. Таким образом, мы проградуировали прямую АВ.

Решим такую же задачу другим способом.

Задача. Проградуировать прямую АВ, заданную проекцией

a16,5 b13,5 .

Решение:

Необходимо определить на проекции данной прямой положение проекций точек с отметками 16, 15, 14.

Параллельно проекции прямой А16,5 В13,5 проведем ряд прямых, отстоящих друг от друга на равном расстоянии произвольной величины, и примем их за линии уровня с отметками 13, 14, 15, 16, 17 (рис. 111). На прямых , - ных к проекции данной прямой и проведённых через точки А16,5 В13,5 , отметим соответственно точку А' на уровне 16,5 и точку В' - на уровне 13,5 , затем соединим их прямой линией. Точки пересечения этой прямой с линиями уровня будут иметь отметки 14, 15, 16. Основания - ров, опущенных из этих точек на проекцию прямой, и будут проекциями точек, имеющих целые отметки 14, 15, 16. Очевидно, что эти точки и делят проекцию прямой на равные отрезки.

78

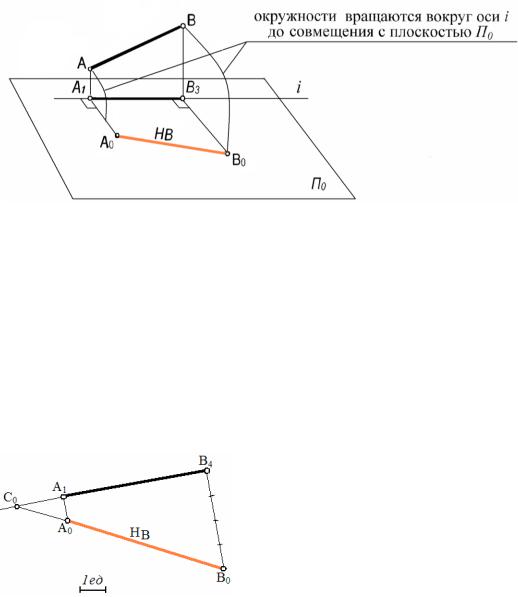
Рис. 111

Описанный способ градуирования прямой при помощи параллельных прямых, проведенных на равных расстояниях друг от друга, положен в основу «палетки», применяемой при наводке горизонталей рельефа местности на картах и планах.

Задача. Определить натуральную величину прямой АВ, угол наклона его к П0 и точку пересечения прямой АВ с плоскостью П0.

Решение:

Рис. 112

Вернемся к чертежу интервалов и уклонов (рис. 112).

Чтобы найти натуральную величину отрезка, отрезок поворачиваем вокруг оси i до совмещения с плоскостью П0. Плоскости вращения каждой точки – это окружности, которые проецируются на плоскость П0 в прямые, перпендикулярные проекции прямой АВ - А1В4. Поэтому из точек А1 и В4 перпендикулярно АВ проводим данные плоскости вращения точек (рис. 113). Градуируем полученные отрезки и соединяем точки А и В между собой. Таким образом, получили натуральную величину отрезка АВ.

Рис. 113

Продолжаем прямую и ее проекцию до их взаимного пересечения и, таким образом, получаем след данной прямой – точку С0.

79

8.6. Взаимное расположение прямых

Положение двух прямых в пространстве может быть определено по их проекциям на плоскость нулевого уровня (П0), если соблюдаются следующие условия:

1.Две прямые в пространстве параллельны, если (рис. 114):

1.заложения прямых параллельны;

2.интервалы заложения ℓ равны;

3.отметки возрастают в одном направлении.

Рис. 114

2. Две прямые в пространстве могут считаться пересекающимися только в том случае, если их проекции имеют общую точку с одноименной числовой отметкой (рис. 115).

Рис. 115

Следствие: любые две горизонтальные прямые, имеющие одинаковые отметки и не параллельные друг другу, взаимно пересекаются. Это положение используется для построения линии пересечения двух плоскостей.

3. Если хотя бы одно из этих условий не выполняется, то прямые

скрещиваются (рис. 116).

Рис. 116

80