метод. НГ краткий курс. 2010

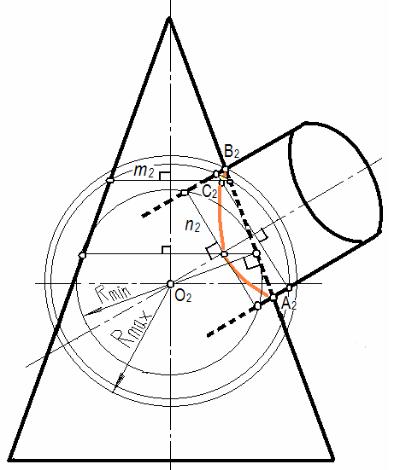
Преимуществом данного метода является возможность решения задачи только на одной плоскости проекций – П2.

Задача. Построить линию пересечения конуса с цилиндром, оси которых пересекаются и параллельны плоскости П2 (рис. 92).

Решение:

Каждая вписанная сфера пересекает заданные поверхности конуса

ицилиндра по окружностям, их проекции на П2 представлены прямыми линиями m и n, которые, в свою очередь, должны быть перпендикулярны соответствующим поверхностям вращения (конуса

ицилиндра). Точка пересечения проекций построенных параллелей С2 принадлежит проекции искомой линии пересечения конуса и цилиндра.

Рис. 92

Rmin вписана в конус и пересекает цилиндр

Rmax - сфера радиусом от точки О2 до точки В2 (расстояние до наиболее удаленной точки линии пересечения).

61

6.7. Теорема Монжа

Теорема: Если две поверхности вращения (второго порядка) описаны вокруг третьей или вписаны в нее, то линия пересечения их распадается на две плоские кривые 2-го порядка. Плоскости этих кривых проходят через точки пересечения линий касания.

Итак, предположим, пересекаются два цилиндра (рис. 93).

Рис. 93

Оси цилиндров пересекаются в точке О. Обе поверхности описаны вокруг третьей – сферы. Сфера пересекает вертикальный цилиндр по окружности m , наклонный цилиндр – по окружности n (в пространстве), на чертеже эти окружности проецируются в прямые, перпендикулярные соответствующим поверхностям . В соответствии с теоремой Монжа, линии пересечения самих цилиндров представляют собой плоские фигуры (эллипсы), которые проходят через общую точку О и точки пересечения линий касания.

Теорема Монжа находит эффективное применение при конструировании трубопроводов. Возможность вписывания сферы в цилиндры одинакового диаметра позволяет очень быстро запроектировать их пересечение.

62

6.8. Пересечение прямой с поверхностью или плоскостью

Задачи на определение точек пересечения прямой с поверхностью (плоскостью) являются основными позиционными задачами начертательной геометрии , а также при построении падающих теней.

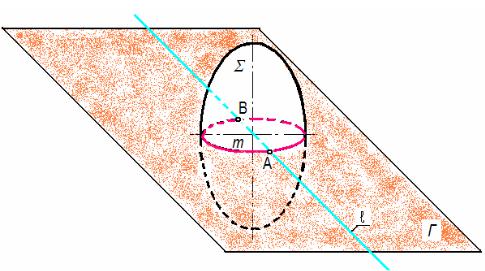
Данные задачи решаются с помощью посредников, в качестве которых используются вспомогательные секущие плоскости. Вид посредника выбирается в зависимости от конкретных условий задачи. Итак, предположим, задана поверхность ∑, в данном случае эллипсоид,, и прямая ℓ (рис. 94). Необходимо построить точки пересечения ∑ и ℓ.

Рис. 94

Алгоритм решения задачи:

1. Через прямую ℓ проводят вспомогательную плоскость посредник Г. ℓ Г

2.Строится линия пересечения вспомогательной плоскости Г с заданной поверхностью ∑ :

Г∩ ∑ m

3.Находятся точки пересечения А и В заданной прямой ℓ с построенной линией пересечения m:

ℓ ∩ m А и В 4. Определяется видимость прямой ℓ.

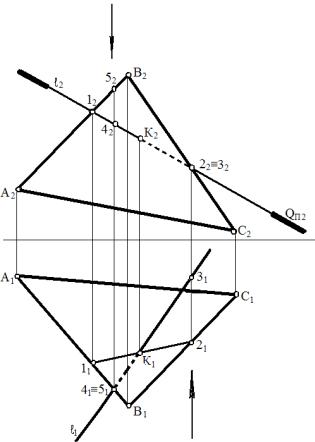
Задача. Построить точку пересечения прямой ℓ с плоскостью общего положения, заданного ∆ АВС (рис. 95).

63

Решение

Алгоритм решения задачи: 1). Выбор посредника:

Q П2 QП2 ℓ

След этой плоскости QП2 совпадает с ℓ2.

2). Построение линии пересечения Q с заданной плоскостью ∆ АВС:

Q ∩ ∑ (12 – 22) (11 – 21) – ЛП

3). Определение точки пересечения прямой с плоскостью - т. К1

т. К2 :

ℓ ∩ (1 - 2) т. К

4).Определение видимости прямой ℓ методом конкурирующих точек.

Рис. 95

64

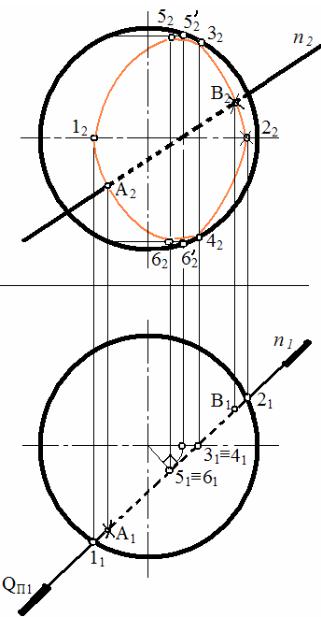
Задача. Построить точки пересечения прямой n с поверхностью сферы (рис. 96).

Решение:

Алгоритм решения данной задачи такой же, как и предыдущей, т.е. через прямую n проводят секущую плоскость-посредник (Q), строят линию пересечения этой плоскости с поверхностью сферы (эллипс). Затем определяют точки пересечения построенного эллипса и прямой n, которые, в свою очередь, и являются точками пересечения прямой n с поверхностью сферы. Далее определяют видимость прямой n.

Рис. 96

65

Раздел 7

7. РАЗВЕРТКИ ПОВЕРХНОСТЕЙ

Построение разверток – это инженерная задача, встречающаяся при выполнении технических деталей из тонкого листового материала, например, кожух вентилятора, воздуховод, патрубки и колпаки в вентиляционной системе и т.д.

Разверткой поверхности называется плоская фигура, получаемая при последовательном совмещении поверхности с плоскостью, без образования складок и разрывов.

К развертываемым относятся все гранные поверхности, а также линейчатые поверхности нулевой кривизны: цилиндрические, конические, торсовые.

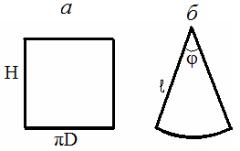
Развертки прямых круговых конусов и цилиндров могут быть выполнены точно. Боковая поверхность цилиндра (рис.97а) представляет собой прямоугольник со сторонами Н, πD. Боковая поверхность конуса (рис. 97б) представляет собой сектор круга, радиус которого равен ℓ - длине образующей конуса, а угол при его вершине = 3600 R / ℓ.

Рис. 97

Развертки наклонного конуса и цилиндра – приближенные. В первый вписывается n–гранная пирамида, во второй – n–гранная призма.

Поверхности вращения (исключая конус и цилиндр) относятся к неразвертываемым поверхностям. Для них строят условные развертки, заменяя части этих поверхностей отсеками развертываемых поверхностей. Подобная замена отсеков одной поверхности отсеками другой, более простой поверхности называется

аппроксимацией.

Т.к. все элементы поверхности на развертке изображаются в натуральную величину, то построение ее сводится к определению натуральных величин элементов заданной поверхности.

Между поверхностью и разверткой существует взаимно однозначное соответствие, т.е. каждой точке поверхности соответствует единственная точка на развертке, и наоборот.

66

7.1.Свойства взаимно однозначного соответствия

1.Прямая на поверхности переходит в прямую на развертке.

2.Параллельные прямые на поверхности переходят в параллельные прямые на развертке.

3.Длины линий на развертке и на поверхности равны.

4.Площадь поверхности равна площади развертки.

7.2. Развертки многогранных поверхностей

Так как все грани многогранной поверхности изображаются на развертке в натуральную величину, построение ее сводится к определению величины отдельных граней поверхностей – плоских многоугольников.

1. Развертка пирамиды.

Задача. Построить развертку пирамиды SАВС. Определить на развертке положение точки М (рис. 98).

Решение:

Итак, для построения развертки поверхности, необходимо знать натуральные величины всех составляющих данной поверхности – образующих и основания.

Основание пирамиды параллельно плоскости П1, поэтому оно уже спроецировано на эту плоскость в натуральную величину:

∆ АВС П1 ∆ А1 В1 С1 – НВ Необходимо найти натуральные величины боковых граней,

вращением вокруг проецирующей оси i1 ≡ S1 .

После определения натуральных величин всех элементов, строится развертка пирамиды.

Для построения точки М на развертке, через данную точку

67

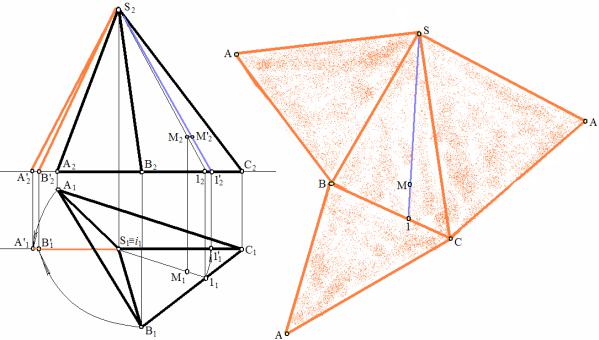
Рис.98

2. Развертка призмы.

При построении развертки боковой поверхности призмы используют 2 способа:

1.способ нормального сечения;

2.способ раскатки.

Способ нормального сечения используется, когда основание призмы является плоскостью общего положения.

Задача. Построить развертку призмы (рис. 99) способом нормального сечения.

Решение:

Ребра заданной призмы располагаются фронтально, поэтому проецируются на плоскость П2 в натуральную величину.

Необходимо определить натуральную величину бокового основания призмы. Для этого перпендикулярно к ребрам призмы

проводим плоскость ∑. ∑П2 А2 А'2 , В2 В'2, С2 С'2.

С помощью преобразования чертежа (в данном случае заменой плоскостей проекций), определяем натуральную величину бокового основания призмы 123.

На свободном месте чертежа проводим линию плоскости нормального сечения ∑, фиксируем точку 1, откладываем последовательно все стороны нормального сечения: 1-2, 2-3, 3-1. Полученный отрезок 1-1 равен периметру нормального сечения призмы.

68

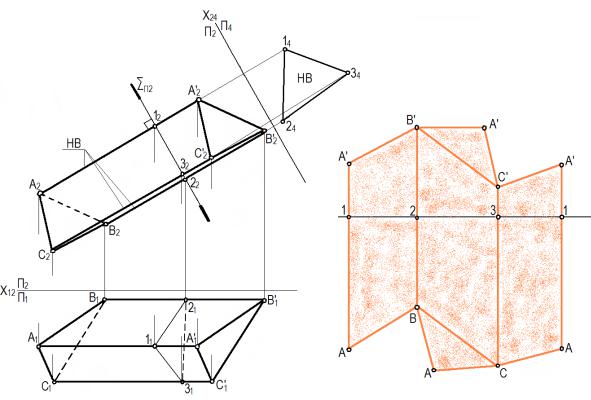
Рис. 99 Через точки 1, 2, 3, 1 проводим прямые, перпендикулярные к линии

∑. Откладываем на этих прямых натуральные величины ребер

призмы: 12 А2, 12 А'2 , 22 В2 , 22 В'2, 32 С2 , 33 С'2 выше и ниже линии плоскости ∑.

Соединяем все полученные точки между собой. Таким образом, построили развертку боковой поверхности призмы.

Далее пристраивают два боковых основания, воспользовавшись натуральными величинами их сторон.

Способ раскатки используется, когда основание призмы параллельно плоскости проекций, где спроецировано в натуральную величину.

Задача. Построить развертку призмы (рис. 100) способом раскатки.

Решение:

Ребра призмы являются горизонталями, поэтому раскатку производят способом вращения вокруг горизонталей и, таким образом, определяются натуральные величины каждой грани призмы.

69

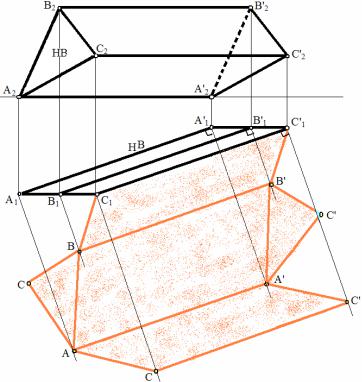
ребер призмы проводим перпендикулярные прямые – плоскости, в которых будут вращаться каждая образующая до положения, когда они совместятся с плоскостью П1. Т. е. вся поверхность призмы превратится в одну плоскость.

Рис. 100

7.3.Развертки кривых поверхностей

Вобщем случае развертки кривых поверхностей выполняются способом триангуляции, т.е. заменой кривой поверхности на вписанную в нее гранную поверхность.

К кривым развертывающимся поверхностям относятся коническая

ицилиндрическая поверхности. В коническую поверхность вписывается пирамидальная, а в цилиндрическую – призматическая поверхность. Строится развертка гранной поверхности, после чего концы ребер соединяются плавной кривой линией.

1. Развертка прямого кругового конуса.

Задача. Построить развертку прямого кругового конуса (рис. 101).

Решение:

Для построения развертки, в поверхность конуса вписывается n-гранная пирамида. Поскольку конус является прямым, то очерковые образующие его являются натуральными величинами поверхности

конуса, и основание спроецировано в плоскости П1 также в

70