ЦОС учебник

обратного преобразования Фурье (2.6) и далее переменим порядок интегрирования:

Заметим, что для допустимости перемены порядка интегрирования достаточно, чтобы подынтегральное выражение (то

Все подынтегральные выражения – периодические, интегрирование идет по периоду, поэтому можно сдвинуть пределы интегрирования для внутреннего интеграла, тогда

= f1 (n ) f2 (n ),

что и требовалось доказать.

2.3Соотношение между спектрами непрерывных и дискретных сигналов

Как уже отмечалось, дискретный сигнал (последовательность) обычно получают посредством дискретизации непрерывного сигнала. Дискретизация оказывает влияние на характеристики сигнала и, в частности, изменяет его спектр. Определим, как соотносятся между собой спектр исходной непрерывной функции времени и спектр полученной из нее последовательности.

33

спектр непрерывного сигнала (прямое преобразование Фурье), а выражение (2.23) дает представление сигнала через спектр (обратное преобразование). Для взаимно однозначного соответствия непрерывного сигнала и его спектра достаточно, чтобы тот и другой были абсолютно интегрируемыми на ( − ∞ , ∞ ), кусочно- непрерывными и кусочно-монотонными.

Чтобы сравнить спектр (2.22) со спектром последовательности (2.5), нужно выразить последний в сопоставимых координатах, то есть задать спектр последовательности в виде функции размерной частоты. Подставляя выражение для частоты (2.1) в формулы (2.5) и (2.6), получаем

В выражениях (2.24) и (2.255) использовано обозначение последовательности, отражающее процесс дискретизации непрерывного сигнала (см. формулу (1.1)). Спектр последовательности в формуле (2.24), в отличие от формулы (2.25),

Установим связь выражений (2.24) и (2.22). Дальнейшие преобразования ведутся в предложении, что функция Fн ограничена

и абсолютно интегрируема на (−∞, ∞) . С учетом формулы (1.1),

перейдем от непрерывного сигнала (2.23) к последовательности

Здесь на втором шаге произведена тождественная замена несобственного интеграла бесконечной суммой интегралов по

Изменим порядок суммирования и интегрирования, отбросим ненужный штрих в обозначении частоты и учтем, что ei 2 π m n = 1 . Тогда

Сравнение полученного выражения с выражением (2.25) выявляет искомое соотношение между спектрами:

Таким образом, спектр последовательности состоит из суммы бесконечного числа спектров непрерывного сигнала, сдвинутых друг относительно друга на 2π .

Если спектр непрерывного сигнала ограничен по полосе частот, то есть

35

Этот факт иллюстрирует Рисунок 2.2. Очевидно, что в данном случае можно однозначно восстановить спектр непрерывного сигнала по спектру последовательности, а следовательно, и сам непрерывный сигнал по дискретному.

Рисунок 2.2 - Пример спектров непрерывного и дискретного сигналов

Если ограничение (2.27) не выполняется, то возникает эффект наложения спектров, выражающийся в том, что высокочастотные составляющие спектра непрерывного сигнала попадают в область более низких частот в спектре последовательности (Рисунок 2.3). Этот эффект всегда нежелателен, поскольку из-за него теряется взаимно однозначная связь спектров; часть информации, содержащейся в непрерывном сигнале, необратимо теряется при дискретизации.

36

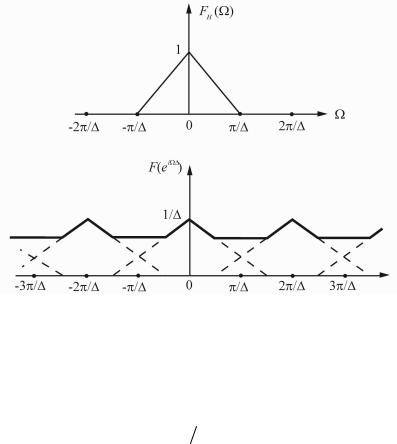
Рисунок 2.3 - Пример спектра непрерывного сигнала и дискретного с наложением спектров

Эффекта наложения можно избежать, если дискретизировать непрерывный сигнал с достаточно высокой скоростью: для выполнения неравенства (2.27) нужно, чтобы верхняя частота Ωв в

спектре непрерывного сигнала была меньше π , или, соответственно, шаг дискретизации

На практике выбирают << πΩв .

Неравенство (2.28) представляет собой ограничение, налагаемое на шаг дискретизации непрерывного сигнала известной теоремой Котельникова.

37

2.4 Практические задания к разделу 2

Частотная характеристика, спектры последовательностей

2.4.1. ЛИС-система с вещественной импульсной характеристикой имеет следующую частотную характеристику:

Найти и изобразить графически импульсную характеристику. Найти реакцию этой системы на входную последовательность

x (n) = cos π n .

3

Зарисовать ИХ, АЧХ и ФЧХ.

x(n) = sin π n . Определить выходную последовательность.

3

2.4.4. Дан спектр вещественной последовательности:

2.4.6. Задана частотная характеристика ЛИС-системы с вещественной импульсной характеристикой:

H (eiω ) = i, 0 < ω < π .

Определить импульсную характеристику. Определить сигнал на выходе системы, если на вход поступает последовательность

x(n) = cos π n .

2

2.4.7. Задана частотная характеристика ЛИС-системы:

H (eiω ) = 1 .

2−cos(ω)

Найти импульсную характеристику. Построить разностное уравнение. Зарисовать структурную схему. Определить реакцию этой ЛИС-системы на единичный скачок.

2.4.8. ЛИС-система описывается разностным уравнением: y (n) = βx (n) + αy (n − 2) .

При каких значениях параметров α,β система устойчива? Определить выходную последовательность, если на вход системы поступает x (n) = cos (n) .

2.4.9. ЛИС-система имеет импульсную характеристику: h(n) = αnu (n) + αn−1u (n −1) + αn−2u (n − 2) .

Найти частотную характеристику. Зарисовать АЧХ и ФЧХ.

2.4.10. ЛИС-система с вещественной импульсной характеристикой имеет частотную характеристику:

H (eiω) = iω, 0 ≤ ω< π .

Найти импульсную характеристику.

2.4.11. ЛИС-система с вещественной импульсной характеристикой имеет частотную характеристику:

H (eiω) = ω, 0 ≤ ω< π .

39

Найти импульсную характеристику. Найти реакцию этой системы на входную последовательность x (n) = 1 + (−1)n .

2.4.12. На вход дискретной ЛИС-системы, описываемой разностным уравнением:

x(n) = sin π n . Определить выходную последовательность. Указание:

3

использовать частотную характеристику.

40

3ОПИСАНИЕ ДИСКРЕТНЫХ СИГНАЛОВ И СИСТЕМ С ПОМОЩЬЮ Z-ПРЕОБРАЗОВАНИЯ

3.1 Прямое z-преобразование

При изучении дискретных сигналов и систем чрезвычайно полезным оказывается представление последовательностей при помощи z-преобразования. Прямым z-преобразованием последовательности f называется комплексная функция

n=−∞

где z – комплексная переменная. Ниже иногда будем использовать сокращенную запись (3.1) в форме f (n) ¾¾z ® F ( z ) . Множество

значений z, для которых ряд (3.1) сходится, и, следовательно, z- преобразование существует и является конечным, называется областью сходимости z-преобразования. Область сходимости зависит от формы преобразуемой последовательности.

Часто в литературе z-преобразование вводится в форме:

∞

F ( z ) = ∑ f ( n) z−n . n=0

Это так называемое одностороннее z-преобразование, которое применяется для последовательностей, заданных только при n ³ 0 . Выражение (3.1) задает более общее двустороннее z- преобразование. С математической точки зрения оно определяет разложение комплексной функции F ( z ) в степенной ряд Лорана.

k =N1

Очевидно, что его область сходимости включает те значения z, при которых все слагаемые в сумме (3.2) конечны, то есть всю

41

Рисунок 3.1а, на котором область сходимости z-преобразования отмечена штриховкой (такой способ изображения областей сходимости будем использовать и в дальнейшем).

Для полубесконечной левосторонней последовательности

( f (n) = 0 при n > N2 ):

n=−∞

В данном случае степенной ряд бесконечен по положительным степеням z. Известно, что такой ряд сходится в круге с центром в начале координат (Рисунок 3.1б), то есть при

должен исследоваться дополнительно для каждого конкретного ряда. Следует заметить, что, если N2 > 0 , то ряд (3.3) содержит и конечное число членов с отрицательными степенями z, в этом случае, очевидно, из области сходимости исключается точка z = 0 .

Для полубесконечной правосторонней последовательности ( f (n) = 0 при n < N1 ) имеем бесконечный ряд по отрицательным степеням z: