
ЦОС учебник
.pdf
Свойство 5. Если двумерная последовательность f вещественна, то ее спектр обладает следующими свойствами центральной симметрии:
Re F (eiω1 , eiω2 )= Re F (e−iω1 , e−iω2 ) ,
Im F (eiω1 , eiω2 )= − Im F (e−iω1 , e−iω2 ) ,
F (eiω1 , eiω2 ) = F (e−iω1 , e−iω2 ) ,
arg F (eiω1 , eiω2 )= − arg F (e−iω1 , e−iω2 ) .
В соответствии со свойствами 4 и 5, линии равных значений вещественной части (или модуля) и мнимой части (или аргумента) спектра двумерной последовательности в плоскости переменных ω1 , ω2 могут выглядеть, например, так, как показано на Рисунке 7.8. Очевидно, чтобы полностью описать такой спектр, достаточно задать его на периоде по одной пространственной частоте и на половине периода по другой, то есть, например, на двумерном "прямоугольном" интервале:
− π1 < ω1 ≤ π , 0 ≤ ω2 ≤ π .
Если вещественная последовательность разделима, то свойства симметрии ее спектра усиливаются, поскольку симметричным является каждый из двух одномерных спектров, входящих как сомножители в (7.28). При этом достаточно рассматривать двумерный спектр на одном квадрате шириной в половину периода, то есть, например, при
|
0 ≤ ω1 ≤ π , 0 ≤ ω2 ≤ π . |
|
|
|||
Свойство 6. |
Свертка |
двумерных |
последовательностей |
|||
соответствует |
произведению |
их |
спектров, |
то |
есть |
|
последовательность (7.13) имеет спектр |
|
|
|
|||
G (eiω1 , eiω2 )= H (eiω1 , eiω2 )F (eiω1 , eiω2 ) . |
|
|
||||
183

Рисунок 7.8 - Линии равных уровней спектров двумерной вещественной последовательности
Из последнего свойства следует, что, как и в одномерном случае,
частотная характеристика H (eiω1 , eiω2 ) полностью определяет
ЛИС-систему, то есть однозначно задает правило преобразования входной двумерной последовательности в выходную (при их описании в частотной области).
184
Остановимся на важном вопросе соответствия между спектром двумерной последовательности и спектром непрерывной двумерной функции, из которой эта последовательность получена. Прямое и обратное преобразования Фурье (переход к спектру и обратно) для непрерывной функции f пространственных переменных x1 , x2 задается соотношением:
Fн(Ω , Ω |
2 |
)= |
∞ |
∞ |
f ( x , x |
)e−i(Ω1x1+Ω2 x2 )dx dx |
2 |
, |
(7.29) |
|||||
|
1 |
|
∫ |
∫ |
1 2 |
|
|
|
1 |
|
|
|||
|
|
|
|
|
−∞ |
−∞ |
|
|
|
|
|
|
|
|
f ( x , x |
)= |
|
1 |
∞ |
∞ |
Fн(Ω , Ω |
|
)ei(Ω1x1+Ω2 x2 )dx dx |
|
|||||
|
∫ |
∫ |
|
, (7.30) |
||||||||||
1 |
2 |
|
4π2 |
1 |
|
2 |
|
1 |
|
2 |
|
|||
|
|
|
−∞ |
−∞ |
|
|
|
|
|
|
|
|
||
где Ω1 , |
Ω2 |
|
|
|
|
|
|
|
|
|
|
|
||
– |
|
угловые |
пространственные |
частоты, |
имеющие |
|||||||||
размерность радиан/единица длины. Из (7.1) и (7.30) выразим двумерную последовательность, полученную в результате пространственной дискретизации непрерывной функции, через
спектр Fн |
этой функции: |
|
|
|
|
|
||
f (n1, n2 )= f (n1 1, n2 2 ) = |
|
|
|
|
|
|||
= |
1 |
∞ ∞ |
Fн(Ω , Ω |
|
)ei(Ω1 1n1+Ω2 2n2 )d Ω dΩ |
. (7.31) |
||
∫ ∫ |
|
|||||||
|
2 |
2 |
||||||
|
4π2 |
−∞ −∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
С учетом значений шагов дискретизации произведем замену |
||||||||
размерных пространственных частот на безразмерные |
ω1 = Ω1 1 , |
|||||||
ω2 = Ω2 2 |
и |
выполним |
несложные |
преобразования |
выражения |
|||
(7.31), заключающееся в разбиении интегрирования, замене переменных и порядка выполнения и суммирования:
f (n1, n2 )= f (n1 1, n2 2 ) =
|
1 |
∞ ∞ |
1 |
|
ω1 |
|
ω2 |
|
|
|
|
|
|
|
|||||||
= |
∫ ∫ |
Fн |
, |
ei(ω1n1 |
+ω2n2 )d ω d ω = |
|||||
|
|
|
||||||||
|
4π2 |
−∞ −∞ |
1 2 |
1 |
|
2 |
|
|||
185

|
|
|
1 |
|
∞ |
|
∞ |
(2k1+1)π (2k2 +1)π |
|
|
|
|
|
|
||||||||
|
= |
|
∑ |
|
∑ |
|
∫ |
∫ |
1 |
|
|
´ |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
4p2 k1=−∞ k2 =−∞ (2k1−1)π (2k2 −1)π D1 D2 |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
+ω2n2 )dw d w = |
|
|
|||||||
|
|
|
|
|
|
|
´ Fн w1 , w2 |
ei(ω1n1 |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
D1 |
|
D2 |
|
|
|
1 |
2 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
1 |
|
π π |
|
1 |
|
∞ |
|
∞ |
|
+ 2pk1 |
|
|
|
w2 + 2pk2 |
|
|
|||||
= |
|
∫ ∫ |
|
|
∑ ∑ |
Fн |
w1 |
|
, |
|
´ |
|||||||||||
|
|
|
|
|
D1 |
|
||||||||||||||||
4p2 |
D1 D2 k =−∞ k |
2 |
=−∞ |
|
|
|
|
D2 |
|
|
||||||||||||
|
|
−π −π |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
´ ei(ω1n1+ω2n2 )dw1 d w2 .
Сопоставление последнего выражения с формулой (7.26) выявляет искомое соотношение между спектрами:
F (eiω1 , eiω2 ) = |
1 |
|
∞ |
|
∞ |
|
+ 2pk1 |
|
w2 |
+ 2pk2 |
|
||
|
∑ |
∑ |
Fн |
w1 |
, |
. (7.32) |
|||||||
D D |
|
|
D |
|
|
||||||||
|
2 k =−∞ |
k |
=−∞ |
|
|
|
D |
2 |
|
||||
|
1 |
1 |
|
|
|
||||||||
|
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
Таким образом, спектр двумерной последовательности формируется как сумма бесконечного числа спектров исходной непрерывной функции, сдвинутых друг относительно друга по переменным w1 , w2 на интервалы, кратные 2p. Данное
суммирование и определяет периодичность спектра последовательности (см. свойство 4).
Если спектр непрерывной функции ограничен, а именно,
Fн |
(W , W |
2 |
) = 0 при |
|
W |
|
³ |
p |
или |
|
W |
2 |
|
³ |
p |
, |
(7.33) |
|
|
|
|
||||||||||||||
|
|
|
|
||||||||||||||
|
1 |
|
|
1 |
|
|
D1 |
|
|
|
|
|
D2 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
то на интервале w1 < p, w2 < p , определяющем период спектра последовательности,
F (eiω1 , eiω2 ) = |
1 |
|
|
|
|
|
|
|
Fн w1 |
, w2 |
. |
||||
D D |
|
||||||
|
2 |
|
D |
D |
2 |
|
|
|
1 |
1 |
|
||||
В этом случае можно однозначно восстановить спектр непрерывного двумерного сигнала по спектру последовательности, а сам непрерывный сигнал – по дискретному.
Если ограничение (7.33) не выполняется, то наблюдается
эффект наложения спектров, выражающийся в том, что
186
высокочастотные составляющие спектра непрерывной функции попадают в область более низких частот в спектре последовательности. Такое наложение нарушает взаимно однозначное соответствие спектров непрерывного и дискретного двумерных сигналов и исключает возможность безошибочного восстановления непрерывной функции по ее отсчетам. Чтобы не допустить эффекта наложения нужно выбрать шаги дискретизации из условий
|
D1 |
< |
p |
|
, D2 < |
p |
, |
|
|
|
|
|||||
|
W1max |
|
W2 max |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
где W1max , |
W2 max – |
максимальные (граничные) пространственные |
||||||||||||||
частоты спектра непрерывного двумерного сигнала: |
|
|
||||||||||||||
Fн(W1, W2 ) = 0 |
при |
|
W1 |
|
³ W1max или |
|
|
W2 |
|
³ W2 max . |
|
|||||
|
|
|
|
|
||||||||||||
7.6 Двумерное z-преобразование |
|
|
|
|
|
|
|
|
||||||||
Прямым z-преобразованием двумерной |
последовательности f |
|||||||||||||||
называется комплексная функция |
|
|
|
|
|
|
|
|
||||||||
|
|
|
∞ |
|
∞ |
|
|
|
|
|
|
|
|
|||
F ( z1, z2 ) = ∑ |
|
∑ f (n1, n2 ) z1−n1 z2−n2 |
, |
(7.34) |
||||||||||||
|
|
n1=−∞ n2 =−∞ |
|
|
|
|
|
|
|
|
||||||
где z1 , z2 |
– комплексные переменные. Ниже |
иногда |
будем |
|||||||||||||
использовать сокращенную запись (7.34) в форме |
|
|
||||||||||||||
f (n1, n2 ) ¾¾z ® F ( z1, z2 ) .
Естественно, данное “ двумерное“ z -преобразование имеет смысл только в своей области сходимости, то есть на множестве таких значений z1 и z2 , при которых сумма (7.34) существует и является конечной. Достаточным условием этого является абсолютная сходимость записанного двойного ряда:
∞ |
∞ |
|
f |
(n1, n2 ) z1−n1 z2−n2 |
|
= |
|
|
|||||
|
|
|
|
||||||||||
∑ ∑ |
|
|
|
|
|||||||||
n1=−∞ n2 =−∞ |
|
|
|
|
|
|
|
|
|
|
|
(7.35) |
|
|
|
|
|
|
|
|
|
|
|
||||
|
∞ |
∞ |
|
|
|
|
|
|
|
||||
|
(n1, n2 ) |
|
|
|
|
−n1 |
|
−n2 < ¥. |
|||||
|
= ∑ ∑ |
f |
|
z1 |
z2 |
||||||||
|
n1=−∞ n2 =−∞ |
|
|
|
|
|
|
|
|
187 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|

Из этой формулы следует важный вывод о том, что область сходимости определяется только абсолютными значениями
комплексных переменных |
|
z1 , |
|
z2 , а значит, может быть задана на |
||||
плоскости в координатах ( |
|
z1 |
|
, |
|
z2 |
|
). Речь идет о внутренних точках |
|
|
|
|
|||||
области сходимости z-преобразования. На границах области условие (7.35) может не выполняться, по ряд (7.34) сходиться неабсолютно (условно). Вопрос о существовании z-преобразования в каждой точке границы области должен исследоваться дополнительно для конкретного ряда. Рассмотрим частные случаи.
Пусть f – двумерная последовательность конечной длины, удовлетворяющая условию (7.7). Тогда ее z-преобразование будет вычисляться как сумма конечного числа слагаемых:
N1 |
N2 |
|
F ( z1, z2 ) = ∑ |
∑ f (n1, n2 ) z1−n1 z2−n2 . |
(7.36) |
n1=M1 |
n2 =M 2 |
|
Очевидно, что область сходимости такого z-преобразования включает в себя те значения переменных z1 , z2 , при которых все
слагаемые в сумме (7.36) конечны, то есть все точки плоскости ( z1 ,
|
z2 |
|
) |
за исключением, |
возможно, некоторых: точки z1 = 0 , если |
|||||||
|
|
|||||||||||
|
N1 > 0 , точки |
|
z1 |
|
= ∞ , |
если M1 < 0 , точки z2 = 0 , если N2 > 0 и |
||||||
|
|
|
||||||||||
точки |
|
z2 |
|
= ∞ , если M 2 < 0 . |
||||||||
|
|
|||||||||||
Этот факт иллюстрирует Рисунок 7.9а, на котором область сходимости z-преобразования отмечена штриховкой.
Пусть двумерная последовательность f разделима (для нее выполняется условие (7.16)). При этом ее двумерное z- преобразование также является разделимым:
∞ |
∞ |
(n2 ) z2−n2 = |
|
F ( z1, z2 ) = ∑ f1 |
(n1 ) z1−n1 ∑ f2 |
|
|
n1=−∞ |
n2 =−∞ |
, |
(7.37) |
= F1 ( z1 )F2 ( z2 )
и, следовательно, область сходимости можно определить по каждой переменной. Известно что одномерное z-преобразование общего вида сходится в кольце, то есть для F1 ( z1 ) и F2 ( z2 ) области
188

сходимости записываются соответственно в форме двойных неравенств:
|
|
|
|
|
(1) |
|
|
|
|
( |
) |
|
|
|
||
|
|
|
|
R− |
< |
|
z1 |
1 |
, |
|
||||||
|
|
|
|
|
|
|
< R+ |
|
(7.38) |
|||||||
|
|
|
|
R(2) |
< |
|
z |
|
|
|
< R( |
2) |
, |
|||
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
− |
|
|
|
2 |
|
|
+ |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
||||||
где R(1) |
, |
R(1) |
, |
R(2) |
, |
|
|
R( |
2) |
– |
|
некоторые |
постоянные, |
|||
− |
|
+ |
|
− |
|
|
|
|
+ |
|
|
|
|
|
|
|
характеризующие границы области сходимости. Система неравенств (7.38) определяет область сходимости разделимого двумерного z- преобразования (7.37). В общем случае эта область имеет прямоугольную форму, (см. Рисунок 7.9б). С конкретизацией одномерных последовательностей, входящих в (7.16), конкретизируется и форма области сходимости z-преобразования. Так, если f1 и f2 – правосторонние последовательности (в частности, если ненулевые отсчеты f лежат в первом квадранте), то область сходимости двумерного z-преобразования (7.37) определяется системой неравенств
|
|
|
|
|
|
z |
|
|
|
> R(1) |
, |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
1 |
|
|
|
− |
|
(7.39) |
|
|
|
|
|
|
|
|
|
|
|
(2) |
|
||
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
z2 |
|
|
|
> R− |
|
|
|||
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
||||||
и, следовательно, имеет вид, показанный на Рисунке 7.9в. |
|||||||||||||
Если |
f |
– |
двумерная |
неразделимая |
бесконечная |
||||||||
последовательность, то область сходимости ее z-преобразования уже не выражается независимо по переменным z1 и z2 . Так, можно
показать, что, если ненулевые отсчеты последовательности сосредоточены только в первом квадранте плоскости аргументов (то есть при n1 ³ 0 и n2 ³ 0 ), то область сходимости z-преобразования
опять задается системой неравенств типа (7.39), однако граница области по каждой переменной зависит от другой переменной:
|
|
|
z |
|
|
|
> R(1) ( |
|
z |
2 |
|
), |
||||||
|
|
|
|
|
||||||||||||||
|
|
|
1 |
|
|
|
− |
|
|
|
|
|
(7.40) |
|||||
|
|
|
|
|
|
|
|
> R(2) ( |
|
|
|
|
||||||
|
|
z |
|
|
|
|
|
z |
|
|
). |
|||||||
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
2 |
|
|
|
− |
|
|
1 |
|
|
|
|||
|
|
|
|
|
|
|
189 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
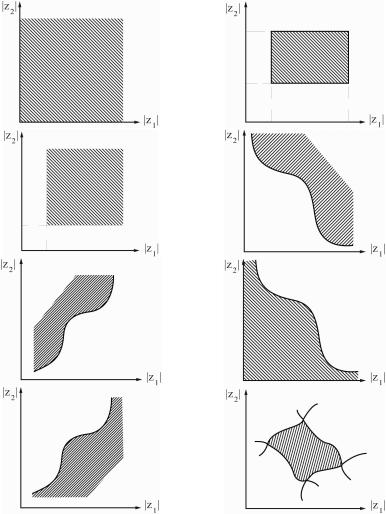
а) |
б) |
в) |
г) |
д) |
е) |
ж) |
з) |
Рисунок 7.9 - Формы области сходимости двумерного z-преобразования: а) последовательность конечной длины, б) разделимая бесконечная последовательность (общий случай), в) разделимая бесконечная
последовательность (правосторонние составляющие), г) произвольная бесконечная последовательность первого квадранта, д) произвольная бесконечная последовательность второго квадранта, е) произвольная бесконечная последовательность третьего квадранта, ж) произвольная бесконечная последовательность четвертого квадранта, з) последовательность, отличная от нуля на всей плоскости аргументов
190
Функции R(1) (×) и |
R2 |
(×) здесь являются взаимообратными, |
|
они |
||||||
− |
− |
|
|
|
|
|
|
|
|
|
определяют границу области сходимости в плоскости ( |
|
z1 |
|
, |
|
z2 |
|
). В |
||
|
|
|
|
|||||||
соответствии с (7.40) эта граница не может иметь участков с положительным наклоном, то есть ограничивает область сходимости снизу и слева (см. Рисунок 7.9г). Здесь и далее условие
взаимообратности |
позволяет |
на |
|
|
|
практике |
ограничиться |
|||||||||||||
использованием любого одного из двух записанных неравенств. |
||||||||||||||||||||
Аналогично, для бесконечной последовательности с ненулевыми |
||||||||||||||||||||
отсчетами во втором квадранте |
|
(при n1 £ 0 , |
n2 ³ 0 ) область |
|||||||||||||||||
сходимости определяется системой неравенств |
|
|||||||||||||||||||
|
|
|
z |
|
|
|
< R(1) ( |
|
z |
2 |
|
), |
|
|||||||
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
1 |
|
+ |
|
|
|
|
|
|
|
|
(7.41) |
|||||
|
|
|
|
|
|
|
|
> R(2) ( |
|
|
|
|
|
|
). |
|||||
|
|
|
z |
|
|
|
|
|
z |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
2 |
|
|
|
− |
|
|
|
|
1 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
при взаимообратных функциях R+(1) (×) и R−2 (×) . Здесь граница области сходимости имеет неотрицательный наклон и ограничивает
область снизу и справа (см. Рисунок 7.9д). |
|
|
||||||||||||||||||||||||||||
Для |
последовательности, |
расположенной |
в третьем квадранте |
|||||||||||||||||||||||||||
(при n1 £ 0 , n2 £ 0 ) имеем |
|
|
|
|
|
< R(1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
z |
|
|
|
|
( |
|
|
|
z |
2 |
|
), |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
1 |
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(7.42) |
||||
|
|
|
|
|
|
|
|
|
|
|
|
< R( |
2) ( |
|
|
|
|
|
|
|
|
). |
|
|||||||
|
|
|
|
|
z |
|
|
|
|
|
|
z |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
+ |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
при взаимообратных R(1) (×) |
и |
|
|
|
|
|
|
|
R(2) (×) , |
область |
сходимости |
|||||||||||||||||||
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
||||||||||
ограничена сверху и справа (см. Рисунок 7.9е). |
|
|
||||||||||||||||||||||||||||
Для |
последовательности |
в четвертом квадранте |
(при n1 ³ 0 , |
|||||||||||||||||||||||||||
n2 £ 0 ) |
|
|
|
|
|
|
|
|
|
|
|
> R(1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
z |
|
( |
|
z |
2 |
|
|
|
), |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
1 |
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1.43) |
|||||
|
|
|
|
|
|
|
|
|
< R( |
2) ( |
|
|
|
|
|
|
|
|
) . |
|
||||||||||
|
|
|
z |
|
|
|
|
|
|
z |
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
2 |
|
|
|
|
+ |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
191

при взаимообратных R−(1) (×) и R+(2) (×) , область сходимости
ограничена сверху и слева (см. Рисунок 7.9ж).
В самом общем случае, когда двумерная последовательность f рассматривается как отличная от нуля на всей плоскости аргументов, ее всегда можно представить в виде четырех составляющих:
f (n1, n2 )= f1 (n1, n2 ) + f2 (n1, n2 ) + f3 (n1, n2 ) + f4 (n1, n2 ) , (7.44)
где fi – последовательности с ненулевыми отсчетами только в i-м квадранте ( i = 1, 2, 3, 4 ). Слагаемые в (7.44) имеют z-преобразования с областями сходимости (7.40) – (7.43). Если эти области имеют общее пересечение, то существует и z-преобразование всей последовательности f, область сходимости которого может быть записана в виде обобщения системы двойных неравенств (7.38):
R(1) ( |
|
|
|
z |
2 |
|
) < |
|
|
|
z |
|
|
|
< R(1) ( |
|
z |
2 |
|
) , |
|
|||||
|
|
|
|
|
|
|
|
|||||||||||||||||||
− |
|
|
|
|
|
|
|
|
|
1 |
|
+ |
|
|
|
|
|
|
|
|
(7.45) |
|||||
R(2) ( |
|
|
|
z |
|
) < |
|
z |
|
|
|
|
< R(2) ( |
|
z |
|
|
) . |
||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
− |
|
|
1 |
|
|
|
|
|
|
2 |
|
|
+ |
|
|
|
|
1 |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
В соответствии с (7.45), любое сечение области сходимости при z1 = const или z2 = const является односвязным, граница области
в общем случае замкнута и состоит из четырех сегментов, два из которых имеют неотрицательный наклон, а два – неположительный. Возможный вид такой области дан на Рисунке 7.9з. Для иллюстрации к сказанному рассмотрим несколько простых примеров.
Пример 7.1. Вычислим z-преобразование двумерной экспоненты первого квадранта (7.4):
f (n1, n2 ) = an1 bn2 u (n1, n2 ) .
Данная двумерная последовательность является разделимой, соотношение (7.6) для нее выполняется при
f1 (n1 ) = an1 u (n1 ) , f2 (n2 ) = bn2 u (n2 ) . z-преобразования и области сходимости приведенных одновременных последовательностей записываются в виде (см. таблицу в п. 1.6.1):
192
