27. Линейная и нелинейная регрессия

Линейная регрессия

Линейная регрессия предполагает, что функция  зависит от параметров  линейно. При этом линейная зависимость от свободной переменной  необязательна,

В случае, когда функция  линейная регрессия имеет вид

здесь  — компоненты вектора .

Значения параметров в случае линейной регрессии находят с помощью метода наименьших квадратов. Использование этого метода обосновано предположением о гауссовском распределении случайной переменной.

Нелинейная регрессия.

Нелинейные регрессионные модели — модели вида

которые не могут быть представлены в виде скалярного произведения

где  — параметры регрессионной модели,  — свободная переменная из пространства ,  — зависимая переменная,  — случайная величина и  — функция из некоторого заданного множества.

28. Матрица (математическая модель) открытой транспортной задачи. Условный потребитель (получатель). Характеристика задач, решаемых этим методом.

Исходные данные задачи могут быть представлены в виде:

• вектора А=(a₁,a₂,...,a_m) запасов поставщиков

• вектора B=(b₁,b₂,...,b_n) запросов потребителей

• матрицы стоимостей (С):

;

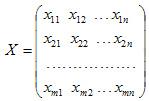
Переменными (неизвестными) транспортной задачи являются x_ij , i=1,2,...,m j=1,2,...,n — объемы перевозок от i-го поставщика каждому j-му потребителю. Эти переменные могут быть записаны в виде матрицы перевозок.

Математическая формулировка транспортной задачи такова: найти переменные задачи X=(xij), i=1,2,...,m; j=1,2,...,n, удовлетворяющие системе ограничений, условиям неотрицательности и обеспечивающие минимум целевой функции.

Область применения: Транспортные задачи линейного программирования тесно связаны с детерминированными динамическими задачами исследования операций, в том числе и с многошаговыми задачами принятия решений в условиях определенности, имеющими большое прикладное значение.

Транспортная задача (или задача прикрепления поставщиков к потребителям) явилась одним из первых примеров оптимизации на линейных сетях. Задача стала типовой для промышленных фирм, имеющих несколько предприятий, складов, рынков сбыта или оптовых баз. Модель главным образом применяется при решении плановых задач. В этом случае стратегические решения сводятся к выбору транспортных маршрутов, по которым продукция различных предприятий доставляется на несколько складов или в различные конечные пункты назначения.

29. Множественная регрессия

Суть регрессионного анализа: построение математической модели и определение ее статистической надежности.

Вид множественной линейной модели регрессионного анализа:

Y = b₀ + b₁x_i1 + ... + b_jx_ij + ... + b_kx_ik + e_i

где e_i - случайные ошибки наблюдения, независимые между собой, имеют нулевую среднюю и дисперсию s.

Назначение множественной регрессии: анализ связи между несколькими независимыми переменными и зависимой переменной.

Экономический смысл параметров множественной регрессии  Коэффициент множественной регрессии b_j показывает, на какую величину в среднем изменится результативный признак Y, если переменную X_j увеличить на единицу измерения, т. е. является нормативным коэффициентом.

Матричная запись множественной линейной модели регрессионного анализа:

Y = Xb + e

где Y - случайный вектор - столбец размерности (n x 1) наблюдаемых значений результативного признака (y₁, y₂,..., y_n);  X - матрица размерности [n x (k+1)] наблюдаемых значений аргументов;  b - вектор - столбец размерности [(k+1) x 1] неизвестных, подлежащих оценке параметров (коэффициентов регрессии) модели;  e - случайный вектор - столбец размерности (n x 1) ошибок наблюдений (остатков).

На практике рекомендуется, чтобы n превышало k не менее, чем в три раза.

Задачи регрессионного анализа  Основная задача регрессионного анализа заключается в нахождении по выборке объемом n оценки неизвестных коэффициентов регрессии b₀, b₁,..., b_k. Задачи регрессионного анализа состоят в том, чтобы по имеющимся статистическим данным для переменных X_i и Y:

• получить наилучшие оценки неизвестных параметров b₀, b₁,..., b_k;

• проверить статистические гипотезы о параметрах модели;

• проверить, достаточно ли хорошо модель согласуется со статистическими данными (адекватность модели данным наблюдений).

Построение моделей множественной регрессии состоит из следующих этапов:

1. выбор формы связи (уравнения регрессии);

2. определение параметров выбранного уравнения;

3. анализ качества уравнения и поверка адекватности уравнения эмпирическим данным, совершенствование уравнения.

Множественная регрессия:

• Множественная регрессия с одной переменной

• Множественная регрессия с двумя переменными

• Множественная регрессия с тремя переменными