
Конспект лекц ТАУ _1ч _11 л
.pdf
71
L( ) 20lg 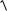
 1 2 / 12 .
1 2 / 12 .
Тем самым ЛАХ и ЛФХ неминимально-фазового апериодического звена отли-
чаются от неминимально-фазового форсирующего звена первого порядка толь-
ко знаком, т.е. симметричны им относительно оси частот (при 1 1, рис. 18).
Рис. 18
Построение частотных характеристик для неминимально-фазового фор-
сирующего звена второго порядка и колебательного звена провести самостоя-
тельно.
1.10 Звено чистого запаздывания
Наряду с рассмотренными типовыми звеньями в передаточную функцию системы также может входить трансцендентное звено чистого запаздывания с передаточной функцией W ( p) e p , где – время запаздывания. При подаче сигнала u(t) на вход такого звена, на выходе, спустя время , формируется сиг-
нал u(t ) . Это следует из теоремы преобразования Лапласа о запаздывании аргумента оригинала. Действительно,
L{u(t )} u(t )e ptdt u(t )e p(t )e p dt
|
|
0 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
p(t ) |
|
p |
|
pt |
|
|
|
p |
|
pt |
|
p |
|
e |
u(t )e |
d(t ) e |
|
dt |
e |
u(t)e |
dt e |
U ( p). |
||||||||
|
|
|
u(t )e |
|
|
|
|
|
||||||||
|
|
0 |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
72
Построим частотные характеристики для звена чистого запаздывания.
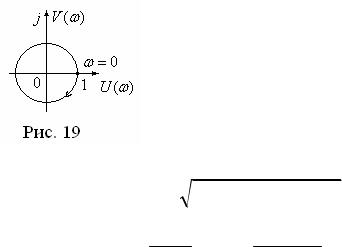
1) Для построения АФЧХ в передаточную функцию подставим p j и
выделим вещественную и мнимую часть:
W ( j ) e j cos( ) jsin( ) U ( ) jV ( ) .
Отсюда следует, что U ( ) cos( ) , V ( ) sin( ) .
На рис. 19 приведен график АФЧХ, из которого следует, что при изменении 0 ФЧХ изменяется ( ) 0.
2) Для построения ЛАХ и ЛФХ воспользуемся форму-
лами
A( ) |W ( j ) | 
 cos2( ) sin2( ) 1,
cos2( ) sin2( ) 1,
( ) arctg V ( ) arctg sin( ) arctg tg( ) .
U ( ) cos( )
Отсюда следует выражение для ЛАХ:
L( ) 20lg1 0.
Таким образом, звено чистого запаздывания не изменяет амплитуду входного сигнала, а вызывает только запаздывание его по фазе.
2. Методика построения ЛАХ и ЛФХ
На основе свойства ЛАХ (3.20) по известным ЛАХ типовых звеньев мож-
но построить асимптотическую ЛАХ для произвольной передаточной функции приведенной к виду (3.14). Алгоритм построения состоит в следующем:
определяется значение 20lg k и отмечается на оси ординат;
определяются сопрягающие частоты i 1/Ti , i 1/ i и вычисляются значения lg i , которые откладываются на оси частот;
строится асимптотическая ЛАХ:
через точку 20lg k проводится слева направо прямая с наклоном 20v
дБ/дек до первой слева сопрягающей частоты, где v – число интегрирующих звеньев в передаточной функции (если v 0, то прямая проводится параллель-
но оси частот; если вместо интегрирующих звеньев присутствуют диффе-
73
ренцирующих звеньев, то следует принять v и наклон асимптоты будет положительным);
в сопрягающей частоте ЛАХ терпит излом относительно предыдущего участка на 20 дБ/дек или 40 дБ/дек. Если сопрягающей частоте соответству-
ет звено первого порядка, то излом составляет 20 дБ/дек, для звена второго по-
рядка (с комплексно-сопряженными корнями) соответственно 40 дБ/дек. Знак
"+" соответствует звеньям, расположенных в числителе, а знак "–" в знаменате-
ле передаточной функции;
далее проводится прямая до следующей сопрягающей частоты, в которой ЛАХ терпит излом аналогично предыдущему;
в области высоких частот ЛАХ уходит в бесконечность с наклоном
20(m n) дБ/дек, где m – порядок числителя, n – порядок знаменателя переда-
точной функции.
На основе свойства ЛФХ (5.19) по известным ЛФХ типовых звеньев мож-
но построить ЛФХ для произвольной передаточной функции приведенной к виду (5.14):
ЛФХ строится в виде суммы ЛФХ типовых звеньев, входящих в переда-
точную функцию, при этом для минимально-фазовых звеньев в области низких частот ЛФХ начинается со значения v / 2 рад, а в области высоких частот ЛФХ стремится к значению (m n) / 2 рад.
По ЛАХ минимально-фазовой системы можно восстановить ее переда-
точную функцию и ЛФХ использую свойства ЛАХ и ЛФХ типовых звеньев.
Для построения АФЧХ по передаточной функции W ( p) в системе MATLAB можно воспользоваться командой nyquist(W), для построения ЛАХ и ЛФХ – командой bode(W) [2].
Вопросы для самопроверки
1. В чем особенность сопрягающей частоты?
74
2.Какой физический смысл имеет безинерционное звено?
3.В чем отличие ЛЧХ дифференцирующего от интегрирующего звена?
4.В чем отличие ЛЧХ форсирующего звена первого порядка от апериодиче-
ского звена?
5.В чем отличие ЛЧХ форсирующего звена второго порядка от колебательно-
го звена?
6.Какой наклон ЛАХ и значение ЛФХ имеет передаточная функция, содержа-
щая два интегрирующих звена?
7.Чем отличаются неминимально-фазовые звенья от минимально-фазовых?
8.Как изменяется сигнал на выходе звена чистого запаздывания?
9.Какое начальное и конечное значение имеет ЛФХ для минимально-фазовых звеньев?
10.От чего зависит наклон ЛАХ в области низких и высоких частот?
75
ЛЕКЦИЯ 6
Структурные схемы САУ и их эквивалентное преобразование. Многомерные систе-
мы.
1. Структурные схемы САУ и их эквивалентное преобразование
Функциональная схема САУ состоит из соединений ФЭ, выделенных от-
дельными блоками, точки обозначают ветвление сигнала, перечеркнутый кру-
жок со стрелками означает суммирование сигнала, если сектор закрашен, то это означает вычитание сигнала. Если ФЭ заменить их передаточными функциями,
то получится структурная схема системы.
Установим правила преобразования структурных схем для основных ви-
дов соединений ФЭ. Для простоты обозначений на структурных схемах вместо изображений Лапласа сигналов будем указывать обозначения их оригиналов, в
передаточных функциях опускать оператор p .
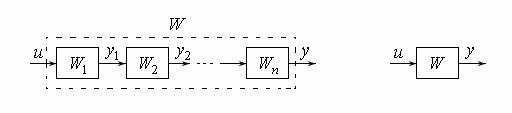
1. Последовательное соединение передаточных функций ФЭ представле-
но на рис. 1, которому соответствует эквивалентная передаточная функция W .
Рис. 1 Рис. 2
В соответствии со структурной схемой имеем следующие зависимости:
y1 W1u , y2 W2 y1, …, y Wn yn 1.
Исключая последовательно промежуточные переменные y1, …, yn 1 получим выражение
y Wn...W2W1u Wu .
Таким образом, для последовательно соединенных передаточных функ-
ций эквивалентная передаточная функция определяется по формуле
n |
|
W ( p) Wi ( p) |
(1) |
i 1 |
|
|
|
76
и структурную схему можно представить с помощью эквивалентного блока со-
гласно рис. 2.
2. Параллельное соединение передаточных функций ФЭ представлено на рис. 3, которому соответствует эквивалентная передаточная функция W .
В соответствии со структурной схемой имеем следующие зависимости:
y1 W1u , y2 W2u , …, y Wnu ,
y y1 y2 ... yn .
Исключая промежуточные переменные y1, …, yn получим выражение
y W1 W2 ... Wn u Wu .
Таким образом, для параллельно соединенных передаточных функций эк-
вивалентная передаточная функция определяется по формуле
n |
|
W ( p) Wi ( p) . |
(2) |
i 1 |
|
|
|
Рис. 3 |
Рис. 4 |
3. Соединение с отрицательной обратной связью передаточных функций ФЭ представлено на рис. 4, которому соответствует эквивалентная передаточ-
ная функция W .
В соответствии со структурной схемой имеем следующие зависимости:
g Wосy, (3) y W .
Исключая промежуточную переменную получим выражение
y W g Wосy ,

77
из которого найдем
y |
W |
g , |
|
||
1 Wраз |
|
|
где Wраз WWос – передаточная функция разомкнутой системы (разомкнутой перед устройством сравнения).
Таким образом, для соединения с отрицательной обратной связью экви-
валентная передаточная функция выхода от входа определяется по формуле
Wyg |
( p) |
W ( p) |
. |
(4) |
|
||||
|
1 Wраз( p) |
|
||
|
|
|
|
|
Для соединений с обратной связью необходимо также знать передаточ-
ную функцию ошибки от входа g . Исключая из уравнений (3) промежуточ-
ную переменную y , получим выражение
g WосW ,
из которого найдем
1 g .
1 Wраз
Таким образом, для соединения с отрицательной обратной связью экви-
валентная передаточная функция выхода от входа определяется по формуле
W g ( p) |
1 |
. |
(5) |
|
1 Wраз( p) |
||||
|
|
|
||
|
|
|
|
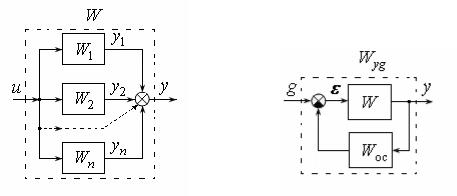
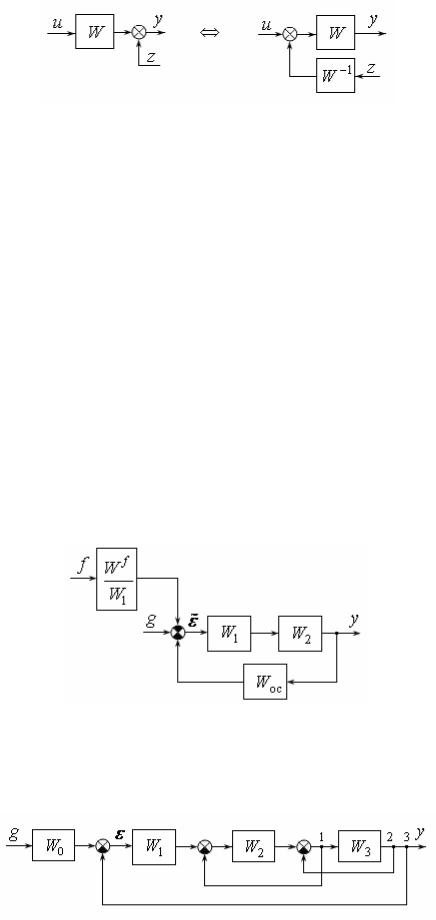
3. Обобщенная структурная схема соединения передаточных функций ФЭ представлена на рис. 5, для которой справедливы следующие зависимости:
Рис. 5
78
Всоответствии со структурной схемой имеем следующие зависимости:
g Wосy,
(6)
y W2 W1 W f f .
Найдем сначала зависимость выхода y от входных сигналов, исключая из уравнений (6) промежуточную переменную . В результате получим уравнение
y W2 W1 g Wосy W f f ,
из которого следует выражение
|
WW |
W f W |
|
||
y |
1 2 |
g |
2 |
f Wyg g Wy f |
f , |
|
|
||||
|
1 Wраз |
1 Wраз |
|
||
с передаточными функциями по каналу "вход-выход"
|
Wyg |
( p) |
W1( p)W2 ( p) |
, |
|
(7) |
||
|
|
|
||||||
|
|
|
|
1 Wраз( p) |
|
|
|
|
и каналу "возмущение-выход" |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
W f ( p)W ( p) |
|
|
|
||
|
Wy f |
( p) |
2 |
|
. |
|
(8) |
|
|
|
1 Wраз( p) |
|
|||||
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
где Wраз( p) W1( p)W2( p)Wос( p) .
Найдем теперь зависимость ошибки от входных сигналов, исключая из уравнений (6) промежуточную переменную y . После аналогичных преобразо-
ваний получим выражение
|
1 |
|
W f W W |
|
|
|
|
|
g |
2 ос |
f W |
g W |
f , |
|
|
|||||
|
1 Wраз |
|
|
g |
f |
|
|
|
1 Wраз |
|
|
||
с передаточными функциями по каналу "вход-ошибка"
|
W g |
( p) |
1 |
, |
|
|
|
(9) |
|
|
|
|
|
||||
|
|
|
1 Wраз( p) |
|
|
|
|
|
и каналу "возмущение-ошибка" |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
W f ( p)W ( p)W ( p) |
|
|
|||
|
W f |
( p) |
2 |
|
ос |
. |
(10) |
|
|
1 Wраз( p) |
|||||||
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
Для облегчения запоминания формул (7)-(10) можно пользоваться сле-
79
дующим правилом: в числителе искомой передаточной функции указывается произведение передаточных функций по пути прохождения выбранного вход-
ного сигнала с учетом знаков сумматоров, через которые проходит сигнал, до заданного выходного сигнала; в знаменателе передаточной функции указывает-
ся выражение 1 Wраз( p) (для отрицательной обратной связи).
Общее правило определения передаточных функций для произвольных структурных схем основано на формуле Мейсона [4, стр. 74]. Однако для про-
стых структурных схем рекомендуется использовать их эквивалентные преоб-
разования с помощью следующих операций.
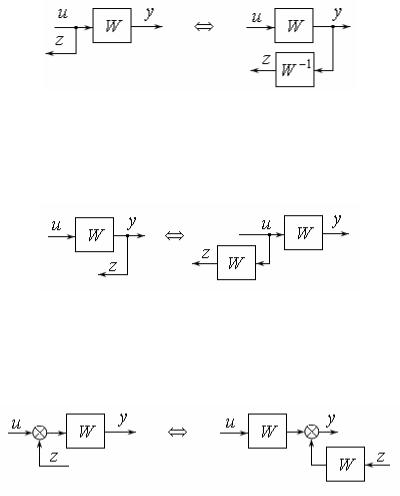
1. Перенос узла через блок по ходу движения сигнала (рис. 6).
Рис. 6
Здесь для левой и правой схемы выполняются равенства: z u и z W 1Wu u . 2. Перенос узла через блок против хода движения сигнала (рис. 7).
Рис. 7
Здесь для левой и правой схемы выполняются равенства: z y Wu и z Wu . 3. Перенос сумматора через блок по ходу движения сигнала (рис. 8).
Рис. 8
Здесь для левой и правой схемы выполняются равенства: y W (u z) и
yWu Wz W (u z) .
4.Перенос сумматора через блок против движения сигнала (рис. 9).
80
Рис. 9
Здесь для левой и правой схемы выполняются равенства: y Wu z и
yWu WW 1z Wu z .
Впроцессе преобразования структурных схем необходимо стремиться привести их к обобщенному виду рис. 5.
Пример 1. Преобразуем структурную схему на рис. 5. Для этого перене-
сем второй сумматор против движения сигнала. Тогда получим эквивалентную
структурную схему рис. 10, где |
и выход y |
связан с входными сигналами |
||||||||
с помощью выражения |
|
|
|
|
|
|
|
|
|
|
|
WW |
|
W f |
|
WW |
W W f |
|
|||
y |
|
1 2 |
g |
|
|
f |
1 2 |
g |
2 |
f , |
|
|
W |
1 W |
|
||||||
1 W |
|
|
1 W |
|
||||||
|
|
раз |
1 |
|
раз |
|
раз |
|
||
которому соответствуют передаточные функции (7), (8).
Рис. 10
Пример 2. Для структурной схемы рис. 11 найти эквивалентную переда-
точную функцию выхода от входа.
Рис. 11
