
Конспект лекц ТАУ _1ч _11 л
.pdf
141
соответствует M 1,58 .
Для построения рис. 8 в системе MATLAB можно использовать команду
nyquist(W);grid
Величина показателя колебательности M может быть определена и в случае использования ЛАХ и ЛФХ. В этом случае граница запретной области
для ЛФХ |
при |
известной ЛАХ строится по показателю |
колебательности |
M const |
(рис. |
7) как отображение полуокружности на |
логарифмическую |
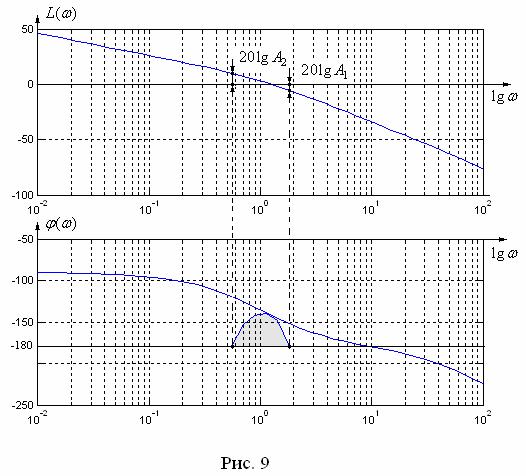
плоскость (рис. 9) с учетом ее расположения относительно АФЧХ W ( j ). По-
рядок отображения состоит в следующем: некоторому значению амплитуды
A1 |W ( j i ) | A2 при частоте i соответствует точка Bi на окружности со зна-
чением модуля A( i ) |W ( j i ) | и фазы 180 i , которая отмечается на гра-
фике ЛФХ.
Пример 2. Для разомкнутой системы с передаточной функцией
k
W ( p)
p(T1 p 1)(T1 p 1)
при k 2 , T1 1с, T2 0,01с построить запретную область ЛФХ при M 1,54 .
Решение задачи в системе MATLAB проведем с помощью Script-файла:
k=2; T1=1; T2=0.01; M=1.54; W=tf([k],[T1 1])*tf([1],[T2 1 0]);
[mag,phase,omega]=bode(W,{0.01,100}); [n,m]=size(omega) subplot(2,1,1);
semilogx(omega,20*log10(mag(:))),grid on subplot(2,1,2); semilogx(omega,phase(:));hold on
for i=1:n; if mag(i)<M/(M+1)|mag(i)>M/(M-1); fi(i)=-180;
else fi(i)=-180+acos((M^2+mag(i)^2*(M^2-1))/(2*mag(i)*M^2))*180/pi; end;
end;
semilogx(omega,fi), grid on
Результат выполнения программы после редактирования представлен на рис. 9, где закрашенная запретная область указывает на то, что замкнутая сис-
тема имеет показатель колебательности M 1,54 .
142
б) Для разомкнутой системы показатели качества замкнутой системы также можно охарактеризовать запасами устойчивости по амплитуде и фазе для ЛАХ и ЛФХ, рассмотренные в лекции 10 (рис. 10, рис. 11). В хорошо демпфи-
рованных системах запасы устойчивости по модулю L1, L2 находятся в преде-
лах от 6 до 20 дБ, а запас по фазе З – от 30 до 60 . Время регулирования tp
замкнутой системы связано с частотой среза разомкнутой системы cp выра-
жением tp b / cp , где b поправочный коэффициент, значение которого зави-
сит от вида вещественной частотной характеристики P( ) замкнутой системы
[9].
3. Интегральные показатели качества позволяют судить о характере переходного процесса по заданному функционалу, зависящего от переходной составляющей ошибки п(t) (t) уст (или отклонения от невозмущенного движения), которая при t стремится к нулю.
143
В качестве функционала наиболее часто используются простейшая J0
или улучшенная J1 интегральная квадратичная оценка:
|
|
|
|
|
|
|
|
|
|
|
|
|
J0 п2 (t)dt , |
|
(8) |
||||
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
2 |
|
2 2 |
|
|
|
J |
1 |
|
|
(t) |
(t) |
dt , |
(9) |
||
|
|
|
п |
|
1 п |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
где 1 0 – весовой коэффициент учитывает скорость п . Аналогично строятся квадратичные оценки, учитывающие ускорение сигнала п(t) и т.д. Оценка (8)
характеризует значение площади под кривой п(t) : чем больше ее величина,
тем хуже качество переходного процесса. В оценке (9) процесс считается наи-
лучшим при наименьших значениях п(t) , п(t) . Это условие является проти-
воречивым, поскольку при малых значениях п(t) процесс п(t) будет затяги-
ваться во времени, что приведет к росту значения J1 . Тем самым, для оценки
(9), в отличие от оценки (8), существует некоторый оптимальный процесс.
Достоинство оценок (8), (9) состоит в том, что по заданному дифферен-
циальному уравнению для п(t) их вычисление можно свести к решению сис-
темы линейных уравнений. Рассмотрим эту процедуру для системы второго по-
рядка.
Пусть дифференциальное уравнение для переходной составляющей
ошибки имеет вид |
|
|
|
п a1 п a2 п 0, |
(10) |
||
для которого введем вектор состояния x [ |
п |
, ]T |
. Тогда систему (10) и оцен- |
|
п |
|
|
ку (9) можно записать следующим образом: |
|
|
|
x Ax, |
|
|
(11) |
|
|
|
|
J1 xT (t)Qx(t)dt , |
(12) |
||
0 |
|
|
|
где

144
|
0 |
1 |
1 |
0 |
|
A |
|
, Q |
12 |
. |
|
a2 |
a1 |
0 |
|
||
Найдем вспомогательную функцию V (x) xT Kx , для которой выполня-
ется свойство V (x) xT Qx . Тогда
|
|
|
V (x)dt dV (x) V (x( )) V (x(0)) |
xT (t)Qx(t)dt |
|
0 |
0 |
0 |
Поскольку при t выполняется условие x(t) 0 , то V (x( )) 0 и, следо-
вательно,
V (x(0)) xT (t)Qx(t)dt .
0
т.е. J1 V (x(0)) xT (0)Kx(0).
С учетом уравнения (11) получим
V (x) xT Kx xT Kx xT AT K KA x xT Qx .
Поэтому для произвольных значений вектора x справедливо равенство |
|
AT K KA Q , |
(13) |
которое называется уравнением Ляпунова относительно неизвестной матрицы
K .
Уравнение (13) обладает свойством
(AT K KA)T AT KT KT A QT Q ,
из которого следует, что матрица KT также является решением уравнения (13).
Следовательно, матрица K KT , т.е. является симметричной.
Для рассматриваемой системы получим уравнение
0 |
a |
k |
k |
|
k |
k |
0 |
1 |
1 |
0 |
||
|
2 |
11 |
12 |
|
11 |
12 |
|
a2 |
|
|
12 |
, |
1 |
a1 k12 |
k22 |
k12 |
k22 |
a1 |
0 |
|
|||||
из которого следуют равенства
2a2k12 1,

145
|
|
|
|
|
|
|
2k 2a k |
22 |
2 , |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
12 |
|
1 |
|
|
|
1 |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
k11 a1k12 a2k22 0. |
|
|
|
|
|
||||||||||||
Отсюда найдем выражение для элементов матрицы K : |
|
|
|
|||||||||||||||||||||
|
|
|
|
1 |
|
|
|
|
1 2a |
|
|
|
|
|
a2 |
(1 |
2a )a |
|
||||||
|
k |
|
|
|
, |
k |
22 |
|
|
|
|
1 2 |
, |
k |
|
1 |
1 2 2 |
. |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
12 |
|
2a2 |
|
|
|
|
2a1a2 |
|
11 |
|
|
2a1a2 |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Если задано начальное условие x(0) [ п(0),0]T , то |
|
|
|
|||||||||||||||||||||
|
|
xT (0)Kx(0) k |
|
|
|
|
a2 |
(1 2a )a |
|
|
|
|||||||||||||
J |
1 |
2 (0) |
1 |
|
|
1 2 |
2 |
2 |
(0) . |
(14) |
||||||||||||||
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
11 |
|
п |
|
|
|
|
|
2a1a2 |
|
п |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
При 1 0 получим выражение для J0 : |
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
a2 a |
2 |
п2 (0) . |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
J |
0 |
|
1 |
|
|
|
|
|
|
(15) |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2a1a2 |
|
|
|
|
|
|
|
|
||||
Известно, что оценка (9) принимает минимальное значение на решении |
||||||||||||||||||||||||
уравнения |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 п п 0 , |
|
|
|
|
|
(16) |
||||||||
которое имеет вид п(t) e t / 1 п(0). Поэтому параметр 1 можно выбрать по заданному времени регулирования tp 3 1, т.е. 1 tp /3.
Из уравнения (10) следует уравнение (16), если положить a1 1a2 и уст-
ремить a2 . В этом случае при a21 0 из уравнения
a21 п 1 п п 0 ,
получим уравнение (16) и оценка J1 1 п2 (0) .
При одних и тех же начальных условиях на рис. 10 приведены переход-
ные процессы для различных значений a2 при a1 1a2 , 1 1, где также ука-
заны соответствующие значения оценки (14).
Таким образом, с помощью интегральных квадратичных оценок (8), (9)
можно не только оценивать качество переходных процессов, но и осуществлять выбор l - вектора настраиваемых параметров системы из необходимых усло-
вий экстремума J1 / i 0, i 1,l .

146
Рис. 10
Для решения уравнения Ляпунова (13) численным методом в системе
MATLAB можно использовать команду K=lyap(A',Q).
Вопросы для самопроверки
1.Что характеризуют основные показатели качества САР?
2.В чем отличие косвенных показателей качества от основных показателей?
3.От чего зависит установившаяся ошибка в замкнутой системы?
4.На чем основаны алгебраические показатели качества?
5.На чем основаны частотные показатели качества?
6.Что означает полоса пропускания системы?
7.Что характеризует частота среза?
8.Что характеризует показатель колебательности?
9. Как связан показатель колебательности с запасами устойчивости по ампли-
туде и фазе АФЧХ разомкнутой системы?
10. Как определяются интегральные квадратичные оценки?
147
СПИСОК ЛИТЕРАТУРЫ
Основная
1. Бесекерский В.А., Попов Е.П. Теория систем автоматического управления. –
С.-Петербург: изд. «Профессия», 2003.
2.Теория автоматического управления / Под ред. В.Б. Яковлева – М.: Высшая школа, 2005.
3.Востриков А.С., Французова Г.А. Теория автоматического управления. –
Высш. шк., 2006. – 365 с.
4. Теория автоматического управления / Под ред. В.И. Лачина – Ростов н / Д:
Феникс, 2007. – 469 с.
5. Воронов А.А. и др. Теория автоматического управления. Ч.1. М., Высш. шк., 1977. – 519 с.
Дополнительная
6. Филлипс Ч., Харбор Р. Системы управления с обратной связью. – М.: Лабо-
ратория Базовых Знаний, 2001. – 616с.
7. Дорф Р. Современные системы управления. – М.: Лаборатория Базовых Зна-
ний, 2002. – 832с.
8. Ким Д.П. Теория автоматического управления. Т.1. Линейные системы – М.:
Физматлит, 2003. – 288 с.
9. Никулин Е.А. Основы теории автоматического управления. Частотные мето-
ды анализа и синтеза систем. – СПб.: БХВ-Петербург, 2004. – 640с.
10. Лурье Б.Я., Энрайт П.Дж. Классические методы автоматического управле-
ния. – СПб.: БХВ-Петербург, 2004. – 640с.
11. Цыпкин Я.З. Основы теории автоматических систем. М.: Наука, 1977. – 560с.
12.Хорн Р., Джонсон Ч. Матричный анализ. М.: Мир, 1989. – 655 с.
13.Медведев В.С., Потемкин В.Г. Control System Toolbox. MATLAB 5 для сту-
дентов. М.: ДИАЛОГ-МИФИ, 1999. – 287с.
14. Дьяконов В., Круглов В. Математические пакеты расширения MATLAB.
Специальный справочник. – СПб.: Питер, 2001 – 480 с.
