
Конспект лекц ТАУ _1ч _11 л
.pdf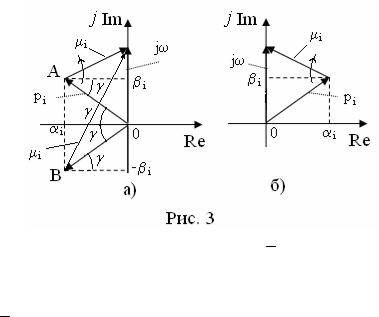
111
2.2. Критерий устойчивости Михайлова
Другой частотный способ определения устойчивости линейной системы связан с построением частотной характеристики D( j ) , которая называется го-
дографом Михайлова, для уравнения (1) при изменении 0 .
Рассмотрим свойства годографа D( j ) с учетом выражения (2):
n |
n |
|
D( j ) | D( j ) | e j arg D( j ) ( j pi ) |
| j pi | e j arg( j pi ) , |
(5) |
i 1 |
i 1 |
|
где |
|
|
n |
|
|
| D( j ) | | j pi |
|, |
(6) |
i 1 |
|
|
n |
|
|
arg D( j ) arg( j pi ) . |
(7) |
|
i 1 |
|
|
Здесь принято обозначение arg( ) – аргумент от комплексного значения, равный значению фазы. На рис. 3 для удобства комплексные значения представлены в виде векторов.
Рассмотрим случай левых корней pi (рис. 3а), где i j pi . Найдем диапазон изменения (приращение) аргумента для функции i j pi при из-
менении 0 . Очевидно, что вектор i (т. А) повернется на угол / 2 .
Для комплексно-сопряженного значения |
p |
i i j i вектор i |
(т. В) по- |
вернется на угол / 2 . Тогда приращение аргумента для |
функции |
||
( j pi )( j pi ) будет равно сумме приращений аргумента для каждого мно-

112
жителя:
arg[( j pi )( j pi )] / 2 / 2 2 /2 .
0
Для вещественного корня ( i 0 , 0 ) получим приращение аргумента
arg[ j pi ] / 2.
0
Рассмотрим случай правых корней pi (рис. 3б). Очевидно, что прираще-
ния аргумента для правых корней будет отличаться только знаком.
Таким образом, левые корни характеристического уравнения (1) дают по-
ложительное, а правые отрицательное приращение аргумента.
На основе проведенного анализа с учетом формулы (7) можно сформули-
ровать следующее свойство.
Свойство. Если характеристическое уравнение (1) имеет m правых и n m
левых корней, то приращение аргумента для годографа Михайлова (5) будет равно:
arg D( j ) / 2(n m) / 2 m / 2 (n 2m) / 2 . |
(8) |
|
0 |
|
|
|
|
|
Отсюда следует, что если построить годограф Михайлова D( j ) |
и опре- |
|
делить из графика его приращение аргумента, равное k / 2 , то из равенства k / 2 (n 2m) / 2 найдем количество правых корней по формуле
m (n k)/ 2. |
(9) |
Если приращение аргумента arg D( j ) n / 2, то |
m 0 и, следова- |
0 |
|
тельно, система устойчива. При этом годограф Михайлова вращается строго против часовой стрелки.
При определении устойчивости системы по приращению аргумента годо-
графа D( j ) необходимо исключать случаи расположения корней на мнимой оси (на границе устойчивости). В этих случаях годограф Михайлова имеет ха-
рактерный вид.
1. Если имеется пара чисто мнимых корней p1,2 j i , то согласно фор-

113
муле (6) при i значение | D( j ) | 0, т.е. годограф Михайлова проходит через начало координат.
2. Если имеется нулевой вещественный корень p1 0, то при 0 зна-
чение | D( j ) | 0, т.е. годограф Михайлова начинается из начала координат.
Отметим, что для устойчивости системы в силу критерия Стодола все ко-
эффициенты характеристического уравнения должны быть положительными,
т.е. в уравнении (1) значение an 0 и годограф Михайлова при 0 должен начинаться на вещественной положительной полуоси.
С учетом указанных свойств теперь можно дать общую геометрическую интерпретацию частотного критерия устойчивости Михайлова:
Для устойчивости системы с характеристическим уравнением (1) не-
обходимо и достаточно, чтобы годограф Михайлова начинался на вещест-
венной положительной полуоси, строго вращался против часовой стрелки,
последовательно обходя n квадрантов (не проходя через начало координат),
и уходил в бесконечность в n -ом квадранте, где n – порядок характеристи-
ческого уравнения.
Для построения годографа Михайлова необходимо:
1)представить D( j ) X ( ) jY ( ) ;
2)найти точки пересечения с вещественной осью, полагая Y ( ) 0 и оп-
ределяя соответствующие положительные значения 1 , 2 , … в порядке воз-
растания;
3) найти точки пересечения с мнимой осью, полагая X ( ) 0 и опреде-
ляя соответствующие положительные значения 1 , 2 , … в порядке возраста-
ния;
4) определить квадрант, в котором годограф уходит в бесконечность по значениям X ( ) , Y ( ).
По полученным точкам пересечения с осями координат в порядке возрас-
тания частоты можно построить годограф Михайлова.
114
Из геометрической интерпретацию критерия Михайлова следует, что для устойчивости системы необходимо и достаточно, чтобы пересечение осей
X ( ) , Y ( ) осуществлялось в последовательности 1 1 2 2 ... и го-
дограф Михайлова уходил в бесконечность в n -ом квадранте.
При нарушении хотя бы одного свойства в формулировках критерия ус-
тойчивости свидетельствует о неустойчивости системы.
Построение годографа Михайлова можно проводить в системе MATLAB
с помощью функции nyquist для полинома D( p) .
Пример 4. Для примера 3 построить годографы Михайлова при значени-
ях k 0, k 5, k 11, k 15 и сделать выводы об устойчивости системы.
Для решения задачи воспользуемся Script-файлом:
T1=1;T2=0.1;
k=0;[u,v,w]=nyquist((tf([T1*T2 T1+T2 1 k],[1])),{1e-8,10}); plot(squeeze(u),squeeze(v));hold on k=5;[u,v,w]=nyquist((tf([T1*T2 T1+T2 1 k],[1])),{1e-8,10}); plot(squeeze(u),squeeze(v)); k=11;[u,v,w]=nyquist((tf([T1*T2 T1+T2 1 k],[1])),{1e-8,10}); plot(squeeze(u),squeeze(v)); k=15;[u,v,w]=nyquist((tf([T1*T2 T1+T2 1 k],[1])),{1e-8,10}); plot(squeeze(u),squeeze(v));grid
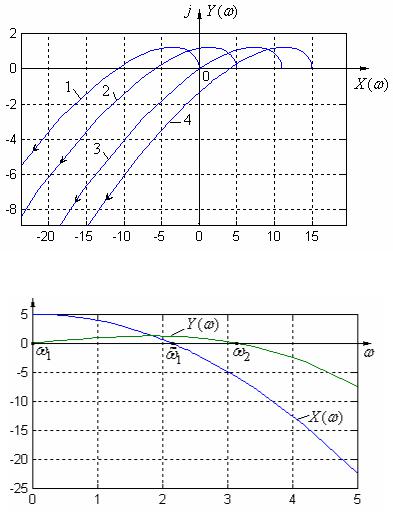
На рис. 4 представлены отредактированные графики годографов Михай-
лова: годограф 1 (k 0) начинается из начала координат и соответствует апе-
риодической границе устойчивости системы; годограф 2 (k 5) последователь-
но обходит три квадранта, что свидетельствует об устойчивости системы; годо-
граф 3 (k 11) проходит через начало координат, тем самым система находится на границе колебательной устойчивости; годограф 4 (k 15) соответствует не-
устойчивой системе.
С помощью команд
k=5;[u,v,w]=nyquist((tf([T1*T2 T1+T2 1 k],[1])),{1e-8,5}); figure(2);plot(w,squeeze(u),w,squeeze(v));grid
проводится построение вещественной X ( ) и мнимой Y ( ) характеристики
для устойчивой системы при k 5 (рис. 5), для которой выполняется условие
чередования корней: 1 1 2 .
115
Рис. 4
Рис. 5
Вопросы для самопроверки
1.Что понимается под критериями устойчивости системы?
2.В чем состоит достаточность критерия Стодола?
3.В чем отличие критерия Гурвица от критерия Стодола?
4.Чем вызваны ограничения использования критерия Гурвица?
5.Как определяется область претендент на устойчивость в методе D-разбиения?
6.Что означает переход через D-кривую из области претендента на устойчи-
вость в соседнюю область?
7.Какими свойствами обладает приращение аргумента годографа Михайлова?
8.Какой вид должен иметь годограф Михайлова, чтобы система была устойчи-
вой, на границе колебательной и апериодической устойчивости?

116
ЛЕКЦИЯ 10
Частотный критерий устойчивости Найквиста. Логарифмический аналог критерия Найквиста. Запасы устойчивости. Устойчивость систем с запаздыванием. Интервальный критерий Найквиста.
1. Частотный критерий устойчивости Найквиста.
В отличие от критерия Михайлова частотный критерий устойчивости Найквиста позволяет судить об устойчивости замкнутой системы по АФЧХ ра-
зомкнутой системы, которая может быть построена аналитически или экспери-
ментально.
Рассмотрим структурную схему замкнутой системы, представленную на рис. 1, которую можно представить в виде рис. 2. Тем самым, замкнутую одно-
мерную систему всегда можно представить в виде рис. 3, где передаточная функция разомкнутой системы W ( p) W1( p)W2 ( p) охвачена отрицательной единичной обратной связью. Далее будем рассматривать такую систему с пере-
даточной функцией W ( p) m( p)/ d( p) , у которой порядок числителя m не превышает порядка знаменателя n , что соответствует условию физической реализуемости.
Для структурной схемы рис. 3 справедливо выражение изображения вы-
хода
Y ( p) W ( p) G( p) , 1 W ( p)
из которого следует уравнение свободного движения системы при G( p) 0:
1 W ( p) Y ( p) 0 .
117
Характеристическое уравнение замкнутой системы определяется из уравнения
1 W ( p) 0 .
Введем вспомогательную функцию |
|
||
F( p) 1 W ( p) |
D( p) |
, |
(1) |
|
|||
|
d( p) |
|
|
где d( p) 0 – характеристическое уравнение разомкнутой системы |
n -го по- |
||
рядка, D( p) d( p) m( p) 0 – характеристическое уравнение замкнутой сис-
темы n -го порядка.
1. Рассмотрим случай, когда характеристическое уравнение разомкнутой системы d( p) 0 имеет m правых и n m левых корней, а характеристическое
уравнение замкнутой системы D( p) 0 |
имеет l правых и n l левых корней. |
|||||
Полагая p j , найдем приращение аргумента функции F( j ) |
при из- |
|||||
менении 0 : |
|
|
|
|
|
|
arg F( j ) arg |
D( j ) |
arg D( j ) argd( j ) |
|
|||
|
(2) |
|||||
0 |
0 d( j ) |
0 |
0 |
|||
|
(n 2l) / 2 (n 2m) / 2 2 (m l)/ 2. |
|
||||
Для устойчивости замкнутой системы необходимо и достаточно, чтобы |
||||||
l 0 и тем самым, |
годограф F( j ) при изменении |
0 должен охваты- |
||||
вать начало координат в положительном направлении m / 2 раз.
Данное условие устойчивости можно переформулировать для АФЧХ ра-
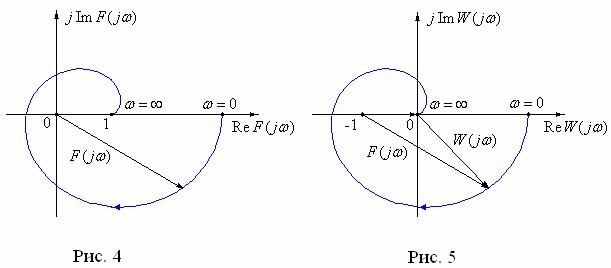
зомкнутой системы W ( j ). На рис. 4 представлен годограф F( j ), вектор

118
которого вращается относительно начала координат. На рис. 5 соответственно представлен годограф W ( j ) F( j ) 1, вектор которого вращается относи-
тельно начала координат, а вектор F( j ) вращается относительно точки
( 1, j0) .
Тем самым, можно сформулировать критерий Найквиста:
Для устойчивости замкнутой системы необходимо и достаточно, чтобы АФЧХ разомкнутой системы W ( j ) при изменении 0 охватывал точку ( 1, j0) в положительном направлении m / 2 раз, где m – число правых корней характеристического уравнения разомкнутой системы.
Из рис. 5 следует, что АФЧХ W ( j ) один раз охватывает точку ( 1, j0) в
отрицательном направлении, т.е. 1 m / 2 . Тем самым замкнутая система неус-
тойчива при любом m .
2. Рассмотрим случай, когда характеристическое уравнение разомкнутой системы d( p) 0 имеет корни, расположенные на мнимой оси. Это означает,
что полином d( p) , согласно теореме Безу, будет содержать множители вида p , p2 *2 , которые приводят к скачкообразному изменению фазы АФЧХ W ( j )
(см. лекция 3). Другими словами передаточная функция W ( p) содержит интег-
рирующие и консервативные звенья. Для использования критерия устойчиво-
сти в полиноме d( p) заменим указанные множители приближенными множи-
телями p , p2 p *2 , где 0 – сколь угодно малое значение. Иначе говоря, корни, расположенные на мнимой оси сдвинули в левую полуплоскость на бесконечно малое значение и тем самым пришли к предыдущему случаю.
При этом АФЧХ приближенной передаточной функции W ( j ) начинается на вещественной оси, изменение фазы происходит непрерывно с бесконечно большим значением модуля |W ( j ) | в окрестности точек 0 и * . К по-
строенной АФЧХ W ( j ) можно применить критерий Найквиста, полагая
0.
119
Таким образом, для использования критерия Найквиста в рассматривае-
мом случае необходимо построить АФЧХ W ( j ) и места разрывов ее характе-
ристики по часовой стрелке (отрицательное приращение фазы) дополнить ду-
гами бесконечно большого радиуса.
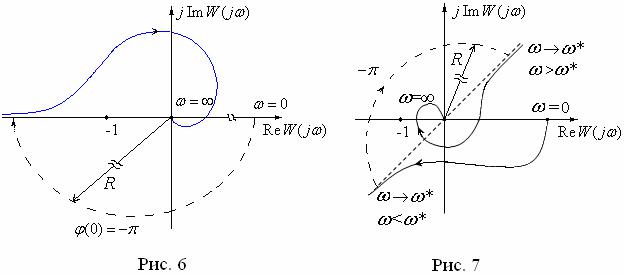
На рис. 6 приведена АФЧХ передаточной функции W ( p) , содержащей два нулевых полюса (два интегрирующих звена). Очевидно, что АФЧХ W ( j ),
дополненная дугой бесконечно большого радиуса R , один раз охватывает точку ( 1, j0) в отрицательном направлении, т.е. 1 m / 2 . Следовательно,
замкнутая система неустойчива при любом m .
На рис. 7 приведена АФЧХ передаточной функции W ( p) , содержащей пару чисто мнимых полюсов (консервативное звено). Очевидно, что АФЧХ
W ( j ), дополненная дугой бесконечно большого радиуса R , один раз ох-
ватывает точку ( 1, j0) в отрицательном направлении, т.е. 1 m / 2 . Следова-
тельно, замкнутая система неустойчива при любом m .
Подсчет охватов удобно проводить с помощью правила Цыпкина, со-
гласно которому число охватов точки ( 1, j0) равно сумме переходов АФЧХ
W ( j ) с учетом знаков вещественной полуоси ( , 1) . На рис. 8 показаны возможные случаи переходов вещественной полуоси ( , 1) . Если АФЧХ
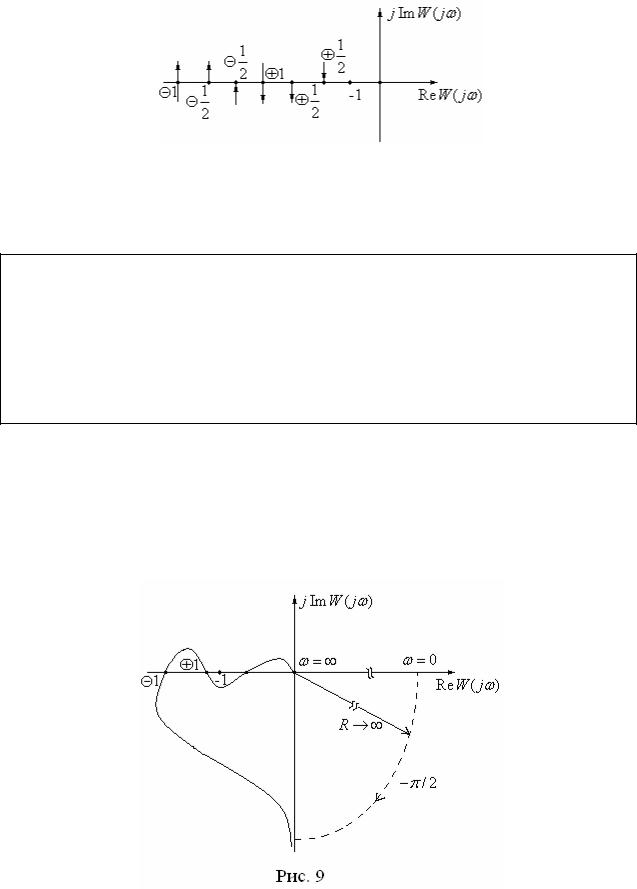
120
W ( j ) касается вещественной полуоси ( , 1) , то это эквивалентно тому, что она совершает два полуперехода с обратными знаками, в сумме равных нулю.
Рис. 8
Тогда критерий Найквиста можно сформулировать так:
Для устойчивости замкнутой системы с единичной отрицательной об-
ратной связью необходимо и достаточно, чтобы АФЧХ разомкнутой системы
W ( j ) при изменении 0 имела в сумме с учетом знаков m / 2 пере-
ходов вещественной полуоси ( , 1) , где m – число правых корней харак-
теристического уравнения разомкнутой системы.
На рис. 6, рис. 7 АФЧХ имеет один отрицательный переход.
На рис. 8 АФЧХ разомкнутой системы имеет отрицательный и положи-
тельный переход, сумма которых равна нулю. Тем самым условие устойчиво-
сти замкнутой системы 0 m / 2 выполняется при m 0.
