
Конспект лекц ТАУ _1ч _11 л
.pdf
|
|
101 |
0 |
1 |
, т.е. представлена в |
Пример 2. Пусть у системы (9) матрица A |
|
|
0 |
0 |
|
виде блока Жордана. Характеристическое уравнение |
|
|||
d( p) | pE A | |
p |
1 |
p2 |
0 , |
n |
|
|
|
|
|
0 |
p |
|
|
имеет кратные корни p1,2 0 . Тогда решение x(t) можно записать с помощью формулы (7.9) в виде
x(t) E2 A(t t0 ) x(t0 ) ,
т.е. x1(t) x1(t0) (t t0)x2(t0 ) , x2(t) x2(t0 ) (рис. 6).
Таким образом, система неустойчивая по Ляпунову.
Отметим, что система примера 1 в отличие от системы примера 2 не мо-
жет быть приведена к дифференциальному уравнению 2-го порядка. Это отра-
жается на устойчивости данных систем.
С учетом сказанного выше следует, корневой критерий устойчивости ли-
нейной системы:
Для асимптотической устойчивости линейной системы необходимо и достаточно, чтобы все корни характеристического уравнения системы имели отрицательные вещественные части, т.е. располагались в левой комплексной полуплоскости. Если имеется хотя бы один корень с положи-
тельной вещественной частью, то система неустойчивая. Если имеются корни, расположенные на мнимой оси, то устойчивость системы по Ляпу-
нову зависит от структуры матрицы системы, т.е. наличия жордановых блоков для данных корней.
При отсутствии жордановых блоков для корней с нулевой вещественной частью и остальных корней, расположенных в левой полуплоскости, система устойчива по Ляпунову. В этом случае также говорят, что система находится на границе устойчивости. При этом в случае нулевых корней система находится
на границе апериодической устойчивости, в случае чисто мнимых корней – на границе колебательной устойчивости.

102
В дальнейшем для краткости асимптотически устойчивую линейную сис-
тему будем называть просто устойчивой. При этом корни характеристического уравнения системы, имеющие отрицательные вещественные части, т.е. распо-
ложенные в левой комплексной полуплоскости, будем называть левыми, а рас-
положенные в правой комплексной полуплоскости – правыми.
Если исходная система имеет вид
x Ax Bu* , x(t |
) x , |
(12) |
0 |
0 |
|
то для исследования устойчивости запишем уравнение системы в отклонении от установившегося режима xуст , который будем считать невозмущенным дви-
жением, удовлетворяющим уравнению
xуст Axуст Bu* . |
(13) |
Из уравнений (12), (13) следует уравнение в отклонении x x xуст от |
|
установившегося режима
x A x , x(t0) x0 xуст .
Отсюда следует вывод:
Устойчивость линейной системы не зависит от вида входного воздей-
ствия, а определяется корнями ее характеристического уравнения.
Системе (12) согласно (6.3) соответствует зависимость «вход-выход»
X ( p) W ( p)U*( p)
|
1 |
|
1 |
|
с передаточной матрицей W ( p) pE |
A |
B |
|
AT ( p)B , у элементов ко- |
|
||||
n |
|
|
d( p) |
|
|
|
|
||
торой знаменателем является характеристический полином d( p) . Поэтому справедливо следующее правило:
Для анализа устойчивости одномерных систем, представленных с по-
мощью передаточных функций, необходимо приравнять к нулю полином ее знаменателя и определить его корни.
Установим связь устойчивости линейной системы по входу с устойчиво-
стью невозмущенного движения. Для этого рассмотрим систему

|
|
|
|
|
|
|
|
|
103 |
|
x Ax Bu , |
x(0) x0 , |
|
(14) |
|||||
полагая u u* u , |
u* 0 , | u j |
| |
u |
j , j |
|
, |
т.е. || u || . Решение сис- |
||
1,m |
|||||||||
темы (14) имеет вид |
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
x(t) eAt x(0) eA(t )B u( )d , |
|
|||||||
|
|
0 |
|
|
|
|
|
||
для которого согласно (10) справедливо неравенство |
|
|
|||||||
|
n |
|
|
t |
n |
|
|
||
|| x(t) || | epit |
| || ci || |
| epi (t ) |
| || ci || d , |
(15) |
|||||
|
i 1 |
|
|
0 i 1 |
|
|
|||
где ci – вектор, зависящий от значений u j . Отсюда следует, что если корни pi , i 1,n левые, то при t интеграл в правой части неравенства (15) огра-
ничен и, следовательно, || x(t) || .
Таким образом, из условия устойчивости невозмущенного движения сле-
дует устойчивость системы по входу. Справедливо и обратное утверждение.
4. Теоремы Ляпунова об устойчивости по линейному приближению.
Возвращаясь к исходной нелинейной системе (8) возникает вопрос об ее устойчивости в зависимости от устойчивости ее линейного приближения – сис-
темы (9). Впервые этот вопрос был поставлен и решен Ляпуновым в 1892 году и сформулирован в виде следующих теорем.
Теорема 1. Если все корни характеристического уравнения линеаризо-
ванной системы (9) левые, то невозмущенное движение нелинейной системы
(8) асимптотически устойчиво.
Теорема 2. Если среди корней характеристического уравнения линеари-
зованной системы (9) имеется правый корень, то невозмущенное движение не-
линейной системы (8) неустойчиво.
Теорема 3. Если характеристическое уравнения линеаризованной систе-
мы (9) имеет левые корни и корни, расположенные на мнимой оси (критиче-
ский случай), то в этом случае нельзя судить об устойчивости нелинейной сис-
темы (8) по линеаризованной системе (9).
Для исследования устойчивости линейных систем с помощью вычисли-
104
тельного пакета MATLAB коэффициенты характеристического уравнения сис-
темы (11) начиная со старшей степени полинома могут быть найдены с помо-
щью команды p=poly(A). Корни характеристического уравнения определяют-
ся с помощью команды roots(p) или команды eig(A).
Например, если требуется определить устойчивость системы с матрицей
|
0 |
1 |
0 |
|
|
|
A |
|
0 |
0 |
1 |
|
, |
|
|
|||||
|
|
|
2 |
|
|
|
|
3 |
1 |
|
|||
то с помощью команд
A=[0 1 0;0 0 1;-3 -2 -1];a=poly(A),p=roots(a)
получим a =
1.0000 1.0000 2.0000 3.0000
p =
0.1378 + 1.5273i
0.1378 - 1.5273i -1.2757
Поскольку комплексно-сопряженные корни имеют положительную веще-
ственную часть, то система неустойчива.
Вопросы для самопроверки
1.Что понимается под устойчивостью системы?
2.В чем отличие устойчивости невозмущенного движения и устойчивости по входу?
3.Какой геометрический смысл имеет устойчивость по Ляпунову?
4.Почему уравнение возмущенного движения в отклонениях от невозмущенно-
го движения является нестационарным?
5.В чем отличие устойчивости по Ляпунову от асимптотической устойчивости?
6.От чего зависит устойчивость линейной системы?
7.В каком случае система находится на границе устойчивости?
8.От чего зависит устойчивость нелинейной системы, имеющей линейное при-
ближение?

105
ЛЕКЦИЯ 9
Алгебраические критерии устойчивости линейных систем: Стодола, Гурвица. Час-
тотные критерии устойчивости: метод D-разбиения построения области устойчивости,
критерий Михайлова.
В инженерной практике не всегда удобно проверять устойчивость линей-
ной системы по корням характеристического уравнения. Это связано в первую очередь с необходимостью использования ЦВМ, поскольку для алгебраических уравнений выше 3-его порядка требуется использование численных методов.
Кроме того, часто требуется определять область устойчивости системы по па-
раметрам. При этом вычисление корней характеристического уравнения для множества значений параметров является нерациональным. В связи э этим воз-
никает задача определения устойчивости системы без вычисления корней, т.е.
определения условий при которых корни характеристического уравнения ле-
вые. Методы решающие указанную задачу называются критериями устойчиво-
сти. В зависимости от метода решения задачи критериями устойчивости делят-
ся на алгебраические и частотные критерии. Алгебраические критерии позво-
ляют судить об устойчивости системы по коэффициентам характеристического уравнения системы, а частотные – по виду соответствующих частотных харак-
теристик.
1. Алгебраические критерии устойчивости.
Пусть задано характеристическое уравнение линейной системы
|
D( p) | pE |
A | a |
pn a pn 1 a 0, |
a 1. |
(1) |
||||||
|
n |
0 |
1 |
n |
0 |
|
|
|
|
|
|
|
1.1. Критерий Стодола. Для устойчивости системы с характеристиче- |
||||||||||
ским уравнением (1) необходимо, чтобы коэффициенты ai |
0 , i |
|
|
. |
|
|
|||||
0,n |
|||||||||||
|
Доказательство. В соответствии с теоремой Безу уравнение (1) можно |
||||||||||
представить в виде произведения множителей, содержащих корни pi , |
i |
|
: |
||||||||
1,n |
|||||||||||
|
D( p) a0( p p1)( p p2 ) ( p pn ) 0. |
(2) |
|||||||||
|
Пусть все корни левые, причем для вещественных корней коэффициенты |
||||||||||
pi |
0 , а для комплексно-сопряженных корней |
pi i j i , pi 1 |
p |
i |
i j i |
||||||
106
множители
( p pi )( p pi 1) p2 ( pi pi 1) p pi pi 1 p2 2 i p i2 i2
имеют полиномы 2-го порядка с положительными коэффициентами, поскольку
i 0 . Тем самым, если раскрыть полином (2) с положительными коэффици-
ентами и привести к виду уравнения (1), то его коэффициенты также будут по-
ложительными. Отсюда следует критерий Стодола.
Очевидно, что возможны случаи, когда некоторые коэффициенты урав-
нения (2) отрицательные, а коэффициенты уравнения (1) положительные, т.е.
критерий Стодола является только необходимым. Однако, если в уравнении (1)
хотя бы один коэффициент ai 0 , то система неустойчива. Это условие являет-
ся достаточным для неустойчивости системы.
1.2. Критерий Гурвица. Для устойчивости системы с характеристиче-
ским уравнением (1) необходимо и достаточно, чтобы матрица Гурвица
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a1 |
|
a3 |
a5 |
|
|
|
0 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a2 |
a4 |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a0 |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Г 0 |
|
a1 |
a3 |
0 |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
0 |
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
имела положительные главные диагональные миноры: |
|
|
||||||||||||||||||||||||||||||
a 0 , |
2 |
|
|
a1 |
|
a3 |
|
0, …, |
n |
| Г | a |
n 1 |
0. |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||
1 |
1 |
|
|
|
a0 |
|
a2 |
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
Рассмотрим частные случаи: |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
1) при n 2 условие устойчивости определяется неравенствами |
|||||||||||||||||||||||||||||||
|
a 0 , |
|
2 |
|
|
|
a1 |
0 |
|
|
|
a a 0, |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
a0 |
a2 |
|
|
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
т.е. |
a0 1 0 , a1 |
0 , |
a2 0, что совпадает с условием критерия Стодола, кото- |
|||||||||||||||||||||||||||||
рый в этом случае дает необходимое и достаточное условие устойчивости. |
||||||||||||||||||||||||||||||||
|
2) при n 3 условие устойчивости определяется неравенствами |
|||||||||||||||||||||||||||||||
|
a 0 , |
|
2 |
|
|
a1 |
a3 |
|
a a |
2 |
a a 0 , |
3 |
a |
2 |
0, |
|||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
a0 |
a2 |
|
|
|
|
1 |
0 |
3 |
|
|
|
3 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
107 |
|
из которых следует, что ai 0 , i |
|
|
и должно выполняться условие a1a2 a0a3 . |
||
1,3 |
|||||
Таким образом, из критерия Гурвица следуют необходимые условия ус- |
|||||
тойчивости Стодола. |
|
|
|
||
Пример 1. Пусть структурная схема САУ имеет вид рис. 1, где |
|||||
|
|
|
W ( p) |
k |
|
|
|
|
|
. |
|
|
|
|
|
||
p(T1 p 1)(T2 p 1)
Требуется определить условие устойчивости замкнутой системы по коэффициенту усиления k .
Для решения задачи составим характеристическое уравнение замкнутой системы, полагая 1 W ( p) 0 . Отсюда получим
D( p) p(T1 p 1)(T2 p 1) k 0
или
|
|
|
|
|
|
D( p) a p3 |
a p2 |
a p a 0, |
|||||
|
|
|
|
|
|
|
0 |
|
1 |
|
2 |
|
3 |
где a |
TT |
0 , |
a T T 0 , |
a |
2 |
1, a |
k 0 . Тогда условие устойчивости |
||||||
0 |
1 |
2 |
|
1 |
1 |
2 |
|
3 |
|
|
|
||
замкнутой системы определяется неравенством |
a1a2 a0a3 или с учетом под- |
||||||||||||
становки |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 k |
T1 T2 |
. |
(3) |
|||
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
T1T2 |
|
||
Критерий Гурвица удобно использовать для систем невысокого порядка
(n 6 ), поскольку с ростом порядка увеличивается объем аналитических вы-
числений. Если требуется определить область устойчивости по одному пара-
метру, то для систем высокого порядка можно воспользоваться символьными вычислениями пакета MATLAB.
Пример 2. Требуется определить область устойчивости системы
|
0 |
1 |
0 |
|
|
x |
|
0 |
0 |
1 |
|
|
x |
||||
|
|
|
1 |
|
|
|
k |
2 |
|||
по коэффициенту k с помощью символьных вычислений.
Для решения задачи воспользуемся следующим Script-файлом:
108
syms p k % символьные переменные n=3; A=[0 1 0;0 0 1;-k -1 -2];
d=poly(A,'p')% определение характеристического уравнения
%вектор коэффициентов характеристического уравнения aa=coeffs(d,p);n1=n+1;for i=1:n1; a(i)=aa(n1-i+1);end
%второй главный диагональный минор матрицы Грвица delta2=[a(2) a(4);a(1) a(3)]
vpa(det(delta2),6)% выражение минора матрицы Гурвица
В результате выполнения данной программы на печать выводятся выра-
жение характеристического уравнения, второй главный диагональный минор матрицы Гурвица и его выражение:
d =
p^3+2*p^2+p+k
delta2 =
[ 2, k] [ 1, 1]
detG =
2.-1.*k
Таким образом, условие устойчивости по коэффициенту k определяется неравенством 0 k 2 .
2. Частотные критерии устойчивости
При значении порядка системы n 6 использование критерия Гурвица связано с решением сложных неравенств. В этом случае для определения об-
ласти устойчивости более эффективным является частотный метод D - разбие-
ния Неймарка, который в отличие от алгебраического метода является числен-
ным методом.
2.1. Метод D-разбиения построения области устойчивости
Сущность метода D – разбиения, предложенного Ю.И.Неймарком, по од-
ному параметру заключается в следующем. Пусть характеристическое уравне-
ние системы имеет вид:
D( p,k) d( p) k m( p) 0 , |
(4) |
где k неизвестный параметр, по которому требуется определить область устой-

109
чивости системы. Из уравнения (4) запишем выражение для параметра k в опе-
раторной форме:
k( p) d( p) . m( p)
При подстановки p j для значений определяется условие на комплексный параметр k( j ), при котором замкнутая система имеет корни на мнимой оси. Построенная кривая D - разбиения k( j ) X ( ) jY ( ) при
разбивает комплексную плоскость на области с различным содер-
жанием устойчивых корней. При переходе из одной смежной области в другую через кривую D - разбиения один вещественный или пара комплексных сопря-
женных корней переходит через мнимую ось. Область, содержащая наибольшее число левых корней называется претендентом на устойчивую область. Для ус-
тановления правила, определяющего область претендент, рассмотрим пример при n 1.
Полагая D( p,k) p k 0, получим k p и, следовательно, k( j ) j ,
X ( ) 0 , Y ( ) . Тем самым кривая D - разбиения k( j ) проходит по мнимой оси и разделяет комплексную плоскость на две области. Из характери-
стического уравнения следует, что система устойчива при k 0, т.е. при
X ( ) 0 . Если нанести штриховку на кривой D - разбиения k( j ) слева при изменении от до , то область устойчивости будет на стороне штрихов-
ки. Тем самым в данной области наибольшее число устойчивых корней (один единственный корень). При переходе из правой полуплоскости (со стороны штриховки) в левую полуплоскость один корень становится неустойчивым и наоборот. Данные свойства также справедливы для n 2.
В общем случае для системы n -го порядка, если суммарное число пере-
ходов корней при переходах из области с наименьшим числом в область с наи-
большим числом левых корней равно n , то область претендент будет областью устойчивости.
Если число таких переходов меньше n , то найденную область претендент
110
необходимо проверить на устойчивость для любого фиксированного вещест-
венного значения параметра k из данной области с помощью какого-нибудь критерия устойчивости. Здесь можно воспользоваться, например, критерием Гурвица с использованием численных методов вычисления главных диагональ-
ных миноров.
Построение области устойчивости по параметру k методом D - разбиения можно проводить в системе MATLAB с помощью функции nyquist для опе-
раторного выражения параметра k( p) .
Пример 3. Для примера 1 требуется построить кривую D-разбиения при значении параметров T1 1с, T2 0,1с.
Для решения задачи воспользуемся командой
T1=1; T2=0.1; nyquist(-tf([T1*T2 T1+T2 1 0],[1]))
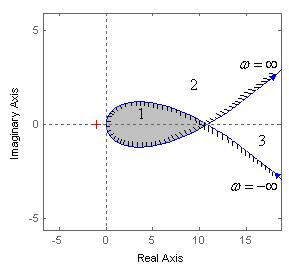
На рис. 2 представлен отредактированный график кривой D-разбиения,
разделяющей комплексную плоскость на три области. При этом область 1 явля-
ется областью претендентом на устойчивость со значением параметра k , удов-
летворяющего неравенству 0 k 11, что совпадает с условием устойчивости по критерию Гурвица (3).
Рис. 2
Метод D-разбиения также применяется для определения областей устой-
чивости по двум параметрам [1].
