
Конспект лекц ТАУ _1ч _11 л
.pdf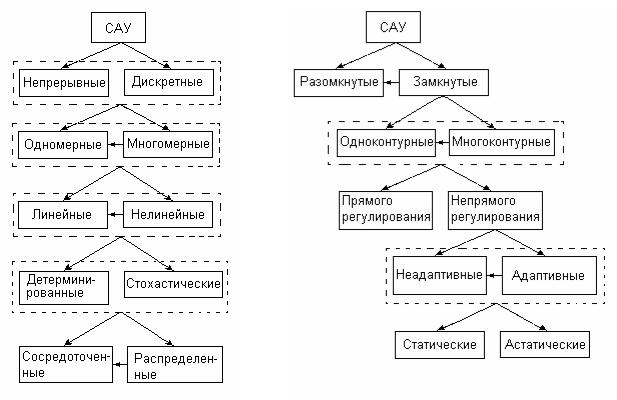
21
распределенной, поскольку в модели ФЭ учитывается его пространственная протяженность. Если ФЭ, проводящий сигнал, можно моделировать материаль-
ной точкой (как это было принято выше), в которой сосредотачиваются все его параметры, то система с такими ФЭ называется сосредоточенной.
В зависимости от использования текущей информации САУ делятся на обычные (неадаптивные) и адаптивные. В отличие от обычных САУ в адап-
тивных текущая информация используется не только для выработки управ-
ляющего сигнала, но и для изменения алгоритма управления и/или задающего воздействия.
Подытоживая выше сказанное можно провести классификацию САУ по виду ее математической модели (рис. 1) и принципу действия (рис. 2). Наиболее простые системы для расчета и реализации, которые разрабатывались на пер-
вом этапе развития ТАУ, соответствуют левым блокам на рис. 1, рис. 2.
Рис. 1 |
Рис. 2 |
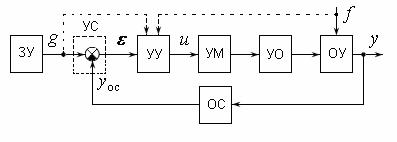
Из предыдущего следует, что замкнутую САУ можно представить в виде одной из обобщенных функциональных схем, представленной на рис. 3, где за-
22
дающее устройство (ЗУ) формирует входной сигнал g , поступающий на уст-
ройство сравнения (УС), на выходе которого формируется ошибка или рассо-
гласование g yос. Известная ошибка и другие сигналы (команда g , воз-
мущение f , отмеченные пунктирной линиями, если их удается измерить) по-
даются в управляющее устройство (УУ), на выходе которого формируется управляющий сигнал u , поступающий в усилитель мощности и затем на управ-
ляющий орган (УО), передающий воздействие на объект управления (ОУ). При этом поведение управляемой величины определяется видом входного воздейст-
вия и свойствами системы.
Рис. 3
В зависимости от характера изменения задающего воздействия g САУ могут быть подразделены на следующие три класса:
1)системы стабилизации;
2)системы программного управления;
3)следящие системы.
В системах стабилизации управляющее воздействие представляет собой заданную постоянную величину: g const (например, система регулирования скорости ДПТ, поддержания заданной температуры жидкости в баке и т.п.).
В системах программного управления известное задающее воздействие может быть функцией времени g(t) gпр(t) (например, для осуществления за-
данного режим нагрева, режим полета ракеты и т.п.) или пространственной ко-
ординатой (например, в системах управления металлообрабатывающих стан-
ков).
В следящих системах задающее воздействие представляет собой заранее неизвестную функцию времени, поэтому предполагается, что измерению дос-
23
тупна ошибка (например, в системе управления радиолокатором по измере-
нию отклонения электронной оси прибора от направления на объект слежения).
В соответствии с представлением системы на рис. 3 рассматривают три основные задачи расчета САУ:
1. Задача идентификации: по известным входным сигналам u, f и вы-
ходному сигналу y определить математическую модель и параметры обобщен-
ного ОУ (ООУ), включающего УМ, УО, ОУ.
2. Задача анализа: при известной математической модели ООУ и при из-
вестных входных воздействиях g, f требуется определить поведение выхода системы y или ошибки замкнутой системы при отсутствии УУ (полагая u ).
3. Задача синтеза: при известной математической модели ООУ, заданном входе g , при ограниченном возмущении f и заданном поведении выхода y
или ошибки найти управляющий сигнал u или алгоритм работы УУ.
Отметим, что в инженерной практике при проектировании САУ на реше-
ние первой задачи уходит две трети времени. При этом следует иметь в виду,
что никакая математическая модель физической системы не является точной.
Она должна адекватно отражать поведение физической системы для заданного режима работы и в то же время быть не слишком сложной для расчета регуля-
тора. Иначе говоря, если с помощью принятой математической модели удается построить регулятор, обеспечивающий требуемый режим работы системы, то данная математическая модель системы является адекватной для выбранного способа расчета и построения регулятора. При этом если регулятор является адаптивным, т.е. настраивается на изменяющиеся параметры ОУ, то очевидно при построении математической модели ОУ могут быть допущены некоторые ее неопределенности.
Решение задачи идентификации ООУ можно проводить на основе экспе-
риментальных данных путем подбора под них соответствующей математиче-
ской модели. Другой способ предполагает разбиение ООУ на отдельные ФЭ,
24
для которых аналитически строятся математические модели и эксперименталь-
но определяются их параметры.
2. Математические модели функциональных элементов
Будем рассматривать в дальнейшем класс динамических систем с сосре-
доточенными параметрами. При этом, следуя законам механики, электротехни-
ки и теплотехники можно считать, что любую систему по характеру динамиче-
ского процесса (степени свободы, обобщенной координаты) можно разбить на ФЭ, представленные с помощью дифференциальных уравнений не выше второ-
го порядка. Наиболее распространенным на практике является уравнение обще-
го вида
F( y, y, y,u,u, f ) 0, |
(1) |
устанавливающее зависимость изменения выходной координаты y , ее скорости
y и ускорения y от входной координаты u и возмущения f . В уравнении (1)
для физически реализуемых систем порядок старшей производной входного
сигнала u или f |
не превышает порядка старшей производной выхода y . Дей- |
ствительно, если |
рассмотреть, например, уравнение F( y,u) y u 0 или |
y u и на вход ФЭ подать линейно нарастающий сигнал u t , t 0, то на вы-
ходе должен возникнуть сигнал y 1. Таким образом, при сколь угодно малом значении входа u на выходе формируется сигнал y 1. Это возможно только при бесконечно большом усилении входного сигнала, что физически не реали-
зуемо.
В зависимости от заданного режима работы системы уравнение (1) может быть упрощено. Так, например, если в системе предполагается реализовать ре-
жим работы, при котором y y* y , u u* u , f f * f , где y* , u* , f * –
соответствуют заданному установившемуся режиму, удовлетворяющему урав-
нению
F* F( y*, y*, y*,u*,u*, f *) 0, |
|
|
|
(2) |
при малых отклонениях (по модулю меньших единицы) y , |
y , |
y , |
u , |
u , |
25
f , то, разлагая функцию F в ряд Тейлора с учетом уравнения (2) и отбрасы-
вая члены разложения выше первого порядка малости, уравнение (1) можно представить в виде:
F( y, y, y,u,u, f ) F* F F a2 y a1 y a0 y b1 u b0 u d0 f 0,
Здесь приняты обозначения для коэффициентов разложения
a |
F |
, a |
F |
, a |
F |
, b |
F |
, b |
F |
, d |
|
|
F |
, |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
||||||||
2 |
y |
1 |
y |
0 |
|
1 |
u |
0 |
|
|
|
f |
|
|||||||||||||
|
|
|
|
|
|
|
|
y |
|
|
* |
|
|
u * |
|
|
|
|
|
* |
||||||
|
|
|
* |
|
|
|
* |
|
|
* |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
(3)
(4)
у которых индекс соответствует порядку производной соответствующей коор-
динаты, нижний знак * означает, что после взятия частных производных полу-
ченные выражения вычисляются для значений y y* , u u* , f f * . Очевидно,
что если y* , u* , f * – функции времени, то коэффициенты (4) также будут функциями времени и уравнение (3) является нестационарным. Отметим, что нестационарное уравнения (3), получено в результате математического преоб-
разования стационарного уравнения (1). В дальнейшем будем рассматривать такие режимы работы системы, при которых коэффициенты уравнения ФЭ (3)
имеют постоянные значения, т.е. уравнение (3) является стационарным.
Таким образом, в условиях принятых допущений от исходного нелиней-
ного уравнения (1) в абсолютных координатах перешли к линейному уравне-
нию (3) в отклонениях от заданного режима, т.е. осуществили линеаризацию
уравнения (1). Допустимость такого перехода обусловлена требованиями к функционированию САУ. Такой подход обоснован, например, при проектиро-
вании САУ тяжелых ЛА и неприемлем для легких ЛА, у которых допускаются большие угловые отклонения и скорости в процессе полета.
Метод линеаризации также не применим для уравнений (1), у которых частные производные терпят разрыв, т.е. некоторые коэффициенты (4) прини-
мают бесконечные значения.
С геометрической точки зрения функция F представляет гиперпло-
скость, касательную к поверхности заданной уравнением (1) в точке y* , y* , y* , u* , u* , f * .
26
Рассмотрим, например, функцию F( y,u) y (u) 0 или y (u) , то-
гда вместо уравнения (3) получим уравнение a0 y b0 u 0 , где
a |
|
F |
1, |
||
|
|
|
|||
0 |
|
|
|
||
|
|
|
y |
|
|
|
|
|
* |
|
|
b |
F |
|
|
k . |
||||
|
|
|
|
|
|
|||
0 |
|
|
|
|
||||
|
|
u * |
|
|
u * |
|
||
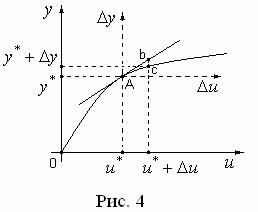
Тем самым получили уравнение в отклонениях y k u , где коэффициент k
определяет угол наклона касательной функции (u) в точке А с координатами
u* , y* (u*) |
(рис. 4). При этом в системе |
|||
координат u , |
y |
функция |
(u) (u*) |
за- |
меняется прямой |
y k u |
с ошибкой |
ап- |
|
проксимации, равной отрезку bc. Отсюда сле-
дует, что чем меньше отклонение u , тем точнее линейная аппроксимация.
Уравнение (3) можно записать в отно-
сительных отклонениях (в безразмерной форме) от заданного режима. Наибо-
лее просто это можно сделать в случае, когда y* , u* , f * – постоянные значения не равные нулю. Для этого надо умножить и поделить каждое слагаемое урав-
нения (3) на соответствующую координату установившегося режима, в резуль-
тате чего будет получено уравнение в относительных координатах y / y* ,
u /u* , f / f * с другими коэффициентами.
Для простоты обозначений в уравнении (3) знак приращения будем
опускать, полагая также a2 1, поскольку на коэффициент a2 |
можно поделить |
||
обе части уравнения. Тогда линейное уравнение (3) запишем в виде |
|||
|
|
|
(5) |
|
y a1y a0 y b1u b0u d0 f . |
||
|
|
|
|
Задачей идентификации ФЭ с уравнением (5) является определение зна-
чений параметров a1 , a0 , b1 , b0 , d0 , например, путем их настройки на физиче-
ской модели ФЭ. Однако из-за наличия в правой части уравнения производной u произвольного входного сигнала непосредственно по уравнению (5) нельзя
27
построить физически реализуемую модель на основе интегрирующих блоков,
использованных ранее при составлении структурных схем.
Для устранения указанного недостатка уравнение (5) перепишем в виде эквивалентной системы двух уравнений первого порядка с помощью вспомога-
тельной переменной z y :
y z,
|
|
z b1u a0 y a1z b0u d0 f . |
|
|
|
|
(6) |
|||||||||
|
|
|
|
|
|
|
||||||||||
Далее с помощью вспомогательных переменных x1 y , |
|
x2 z b1u уравнение |
||||||||||||||
(6) с учетом замены z x2 |
b1u перепишем в виде: |
|
|
|
|
|
||||||||||
|
|
x1 x2 b1u, |
|
|
|
|
|
|
|
|
|
(7) |
||||
|
|
x2 a0x1 a1x2 (b0 a1b1)u d0 f , |
|
|
||||||||||||
|
|
|
|
|
||||||||||||
или в матричной форме |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
(8) |
||||
|
|
|
|
|
|
x Ax bu df , |
|
|
|
|
||||||
|
|
|
|
|
|
y cT x , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
– n -векторы; cT n - вектор- |
||||||||||||
где x – n - вектор (n 2); |
A n n - матрица; b, |
d |
||||||||||||||
строка («т» – символ транспонирования): |
|
|
|
|
|
|
|
|
|
|||||||
x1 |
0 |
|
1 |
|
b1 |
|
|
0 |
, c |
T |
|
|||||
x x |
, |
A a |
0 |
a |
, b |
b a b |
|
, d d |
0 |
|
|
[1 0]. |
||||
2 |
|
|
1 |
|
0 |
1 1 |
|
|
|
|
|
|
|
|||
Здесь размерность n вектора x совпадает с порядком дифференциально- |
||||||||||||||||
го уравнения (5), при этом выход y |
однозначно связан с вектором x , который |
|||||||||||||||
называется вектором состояния, область возможных значений которого назы-
вается пространством состояний.
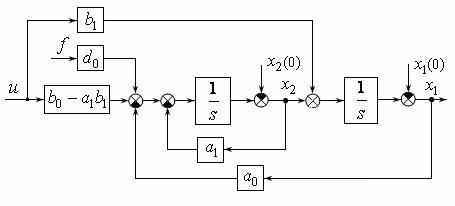
Уравнения (7) или (8) не содержат производных от входных сигналов, по-
этому по ним можно построить структурную схему с помощью интегрирующих блоков (рис. 5) для начальных условий x1(0) y(0) , x2(0) y(0) b1u(0) и при необходимости составить электрическую модель ФЭ, а также получить числен-
ное решение x(t) , t 0 на ЦВМ.
28
Рис. 5
Следует отметить, что для определения аналитического решения y(t) , t 0 уравнения (5) при заданных функциях u(t) , f (t) нет необходимости для перехода к уравнению (8). Для этого можно воспользоваться, например, мето-
дом на основе преобразований Лапласа [2, 11].
С помощью преобразований Лапласа также удается существенно упро-
стить форму записи дифференциального уравнения (5) и использовать это свойство для преобразования структурных схем САУ.
3. Преобразование Лапласа.
Будем |
полагать, |
что функции u(t) , удовлетворяющей условию |
| u(t) | Mect |
при M 0 и |
c 0, ставится в соответствие изображение L{u(t)} |
или одностороннее преобразование Лапласа U ( p), определяемое выражением
|
|
L{u(t)} U ( p) u(t)e ptdt |
(9) |
0 |
|
|
|
от комплексной переменной p j , определенной при любых p таких, что
Re p c . В этом случае подынтегральное выражение в (9) стремится к 0 при t и, следовательно, интеграл сходится. В выражении (9) нижний предел интегрирования рассматривается для момента времени t 0 0 при сколь угодно малом значении 0. Это необходимо для учета предначального зна-
чения функции u(t) , которое обозначается u( 0). Например, для функции u(t) cost значение u( 0) 1.
29
По изображению U ( p) с помощью обратного преобразования Лапласа
|
1 |
j |
|
|
L 1{U ( p)} u(t) |
U ( p)eptdp , |
(10) |
||
2 j |
||||
|
j |
|
||
|
|
|
||
определяется единственная функция |
u(t) |
при выполнении условия |
u(t) 0, |
t 0. Такая функция, удовлетворяющая условиям сходимости интеграла (9),
называются оригиналом. В формуле (10) путь интегрирования в комплексной
плоскости p выбирается правее особых точек изображения U ( p), при которых
оно обращается в бесконечность. Учитывая сложность вычисления интеграла
(10) обратное преобразование Лапласа L 1{U ( p)} определяют с помощью таб-
лиц соответствия оригиналов и изображений (Приложение 1).
Таким образом, смысл преобразования Лапласа (9) заключается в том, что функции времени u(t) ставится в соответствие алгебраическое выражение от
переменной p .
|
Пример 1. Рассмотрим единичную функцию |
|
|
|
|
равную: |
1 при |
|||||||||||||||||||||||||||
|
u(t) 1(t), |
|||||||||||||||||||||||||||||||||
t 0; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 при t 0, с предначальным значением u( 0) 1. Функция u(t) 1(t) яв- |
||||||||||||||||||||||||||||||||||
ляется оригиналом, для которого выполняется |
неравенство |
|
|
ct |
при |
|||||||||||||||||||||||||||||
|1(t) | Me |
|
|||||||||||||||||||||||||||||||||
M 1 |
и c 0. Тогда согласно |
(9) при c 0 |
с учетом равенства | e j t | 1 |
|||||||||||||||||||||||||||||||
получим: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
pt |
|
1 |
|
|
pt |
|
|
|
|
1 |
|
|
|
( j )t |
|
|
|
( j )t |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
L 1(t) |
1(t)e |
|
dt |
|
e |
|
|
|
0 |
|
|
|
lim |
e |
|
|
|
|
lim |
e |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
0 |
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
p t |
|
|
|
|
|
t 0 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
t |
|
j t |
|
|
|
t |
|
|
j t |
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|
||||||
|
|
|
lim e |
|
e |
|
|
|
lim e |
|
|
e |
|
|
|
|
0 1 |
|
. |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
p |
p |
|
|
|
|
|
|
||||||||||||||||||
|
|
p t |
|
|
|
|
|
|
t 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Пример 2. Рассмотрим единичную ступенчатую функцию или единичный скачок, которая определяется по формуле
|
1 при |
t 0, |
(11) |
|
1(t) |
t 0. |
|
|
0 при |
|
|
|
|
|
|
В отличие от единичной функции 1(t) единичный скачок 1(t) терпит раз- |
|||
рыв при t 0, поскольку 1( 0) 0 и 1( 0) 1. При этом функция 1(t) является

30
оригиналом, удовлетворяющая тем же ограничениям, что и функция 1(t). В
этом случае преобразование Лапласа определяется через предел по формуле:
L 1(t) lim |
|
|
|
1 |
|
|
|
||||
1(t) e ptdt |
|
lim e p t |
|||||||||
|
|||||||||||
|
|
|
0 |
|
|
|
p 0 |
|
|||
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
||
|
1 |
lim |
|
е pt |
ep |
|
1 |
е pt |
|||
|
|
|
|
|
|||||||
|
|
lim |
|
|
|
|
lim |
||||
|
p 0 t |
|
|
p t |
|||||||
1 1 0 1 1 ,
p p
т.е. совпадает с изображением Лапласа для единичной функции 1(t).
Таким образом, одному и тому же изображению соответствуют разные функции, значения которых отличаются только в точке t 0. Следовательно,
изображению Лапласа соответствует единственный оригинал для значений
t 0 с начальным условием |
u( 0) |
в момент времени t 0, т.е. при подходе |
|||||||||||||||||||||||||
справа к точке t 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
Пример 3. Аналогично определяется изображение для функции u(t) еat , |
||||||||||||||||||||||||
удовлетворяющего неравенству | еat | Mect |
|
при |
M 1 |
и c a . Тогда согласно |
|||||||||||||||||||||||
(9) при c a или a 0 получим: |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
( a j )t |
||
|
|
at |
|
at |
|
pt |
|
|
(p a)t |
|
|
|
( p a)t |
|
|
|
|
|
|
( a j )t |
|||||||
L е |
|
е |
e |
|
dt |
e |
|
dt |
|
|
e |
0 |
|
|
|
lime |
lim e |
|
|||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
0 |
|
|
|
0 |
|
|
|
p a |
|
|
|
|
|
p a t |
|
|
t 0 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
1 |
|
( a)t |
|
j t |
|
( a)t j t |
1 |
|
0 1 |
1 |
|
|
|
|
||||||||||
|
|
|
|
lime |
|
e |
|
lim e |
|
e |
|
|
|
|
|
|
. |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
p a t |
|
|
|
|
t 0 |
|
|
|
|
p a |
|
|
|
p a |
|
|
|||||||||
Вопросы для самопроверки
1.В чем отличие линейных систем от нелинейных систем?
2.На какие классы делятся САУ в зависимости от вида входного сигнала?
3.В чем состоит задача идентификации САУ?
4.По каким признакам определяется ФЭ?
5.При каких условиях допустима линеаризация нелинейных ФЭ?
6.В каких случаях необходимо представлять ФЭ в пространстве состояний?
7.Каким условиям должен удовлетворять оригинал и почему?
8.Какой единственный оригинал соответствует изображению Лапласа?
