Конспект лекц ТАУ _1ч _11 л

41

Пример 8. Найдем передаточные функции для системы стабилизации скорости по уравнениям (1.6), (1.7), (1.9), из которых с учетом преобразования Лапласа при нулевых начальных условиях получим алгебраические уравнения

Uу( p) Lя p Rя Iя( p) cе ( p) ,

Jp ( p) cмIя( p) Mc ( p) .

Исключая промежуточную переменную Iя( p) , получим выражение для ( p):

записаны в стандартном виде, т.е. когда свободные члены полиномов числи-

теля и знаменателя не нулевой степени имеют значение единица. Удобство та-

кой формы записи заключается в том, что коэффициенты, стоящие при опера-

торах p , имеют размерность секунда в степени соответствующего оператора p . Действительно, уравнению (21) с учетом обратного преобразования Лапласа соответствует дифференциальное уравнение

Tдв kдвuу kдвf Mc ,

из которого следует, что коэффициент Tдв , называемый постоянной времени,

имеет размерность секунда. При этом коэффициенты kдв , kдвf согласовывают размерность входного и выходного сигналов и называются коэффициентами передачи. Если у этих коэффициентов нет размерности, то они называются ко-

эффициентами усиления.

42

Если в числителе и знаменателе передаточной функции W ( p) в изобра-

жениях Лапласа имеются одинаковые множители или, иначе говоря, одинако-

вые нули и полюса, то при определении оригинала y(t) по изображению (19)

допускается сокращение указанных множителей. Однако следует иметь в виду,

что после сокращения общих множителей, понижается порядок передаточной функции и соответствующее ей дифференциальное уравнение отличается от исходного уравнения. Поэтому нельзя упрощать выражение передаточной функции, если эта операция математически не обоснована

Таким образом, передаточная функция W (s) в символьном виде и в изо-

бражениях Лапласа W ( p) совпадают с точностью обозначения s p , если не проводятся сокращения в передаточной функции W ( p) .

Вопросы для самопроверки

1. Чем отличаются изображения операций дифференцирования и интегрирова-

ния оригинала?

2.Какой оригинал соответствует произведению изображений?

3.В чем особенность начального значения оригинала, определяемого по из-

вестному его изображению?

4. В каких случаях по известному изображению можно найти конечное значе-

ние оригинала?

5. При каких условиях решения оригиналов являются асимптотически устойчи-

выми?

6. При каких начальных условиях определяется передаточная функция в преоб-

разованиях Лапласа?

7.В чем отличие передаточных функций в символьном виде и в изображениях Лапласа?

8.В каком случае передаточные функции в символьном виде и в изображениях Лапласа совпадают?

43

ЛЕКЦИЯ 4

Структура движения системы. Типовые входные сигналы. Временные характери-

стики. Частотные характеристики. Свойства АФЧХ. Логарифмические частотные ха-

рактеристики и их свойства.

1. Структура движения системы.

В задачу анализа динамики САУ входит исследование движения системы,

т.е. изменение состояния системы во времени. Движение системы складывается из ряда составляющих, порождаемых различными причинами. Для пояснения сказанного рассмотрим реакцию ФЭ, для которой изображение Лапласа опре-

соответствует свободному движению yсв(t) , вызванному ненулевыми началь-

ными условиями выходной координаты y(t) ,

соответствует вынужденному движению увын(t), вызванному входным воздей-

ствием u(t) с учетом его начальных условий.

Если изображение входного сигнала U ( p) m( p)/ d( p), то выражение (4)

с помощью формулы разложения (2.21) или (2.24) можно представить в виде

44

Выражение (5) можно записать следующим образом

где

соответствует собственному движению yсоб(t) , вызванному входным воздейст-

вием, но независящего от его вида,

уст d( p)

соответствует установившемуся движению yуст(t), зависящего только от вида входного воздействия (полюсов уравнения d( p) 0 ).

Таким образом, структура полного движения выхода y(t) ФЭ с учетом

обратного преобразования Лапласа можно представить следующим образом

i 1,n, поэтому спустя некоторое время, называемое временем установления переходного процесса ty (или временем регулирования tр ), будет выполняться условие y(t) yуст(t) при t ty для произвольного входа u(t) .

Если имеются полюса pi , у которых Re pi 0 , то согласно свойству 2.2 с

течением времени решения yсв(t) , yсоб(t) расходятся и определить yуст(t) по измерениям выхода y(t) для произвольного входа u(t) не удается. Однако для

45

известного входа u(t) в этом случае можно подобрать начальные условия y(0), y(0), u(0), при которых в числителе изображения (1) появятся нули, равные не-

устойчивым полюсам. Тогда после сокращения общих множителей в решении

(9) будут отсутствовать указанные полюса и с течением времени y(t) yуст(t)

при t ty . Однако при этом малые изменения начальных условий, вида входно-

го сигнала, а также параметров системы приводят к проявлению свойства неус-

тойчивости системы. Отсюда следует важный вывод:

Для определения свойств асимптотической устойчивости движения сис-

темы с помощью эксперимента необходимо учитывать произвольные на-

чальные условия, произвольные входные воздействия, а также малые изме-

нения параметров системы.

2. Типовые входные сигналы.

Одним из способов анализа движения системы на практике является по-

строение ее реакции выхода на типовые входные воздействия u(t) , при нуле-

вых начальных условиях (значениях входа, выхода и их производных). В каче-

стве типовых входных воздействий используются сигналы, соответствующие изучаемому свойству системы.

Различают следующие типовые сигналы.

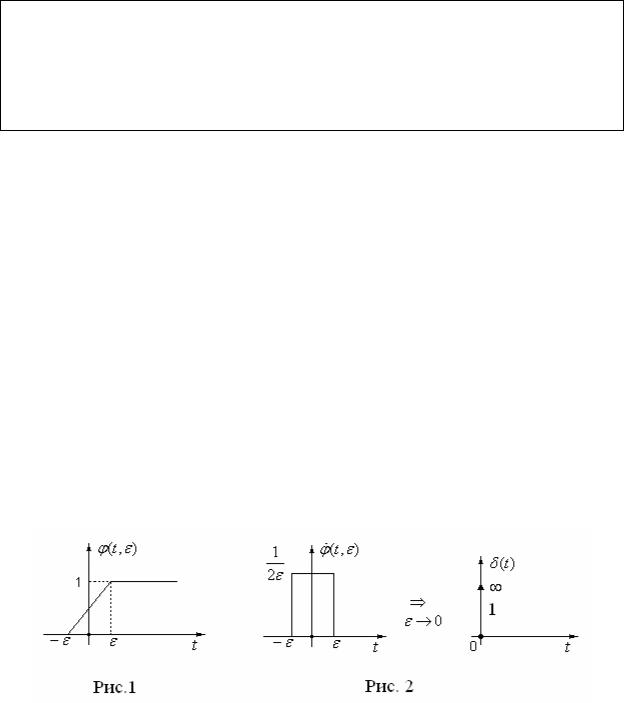
1) Единичный скачок 1(t) , который с физической точки зрения можно

рассматривать, как предел lim (t, ) 1(t) функции (t, ), указанной на рис. 1.

0

Единичный скачок 1(t) используется для имитации скачкообразного из-

менения команды или возмущения.

46 2) Импульсная функция (t) , являющаяся пределом прямоугольного им-

На графиках - функция обозначается стрелкой со знаком бесконечности ее значения амплитуды и единицей – значения площади импульса. Данная функ-

ция используется для имитации короткого ударного воздействия.

Установим связь единичного скачка 1(t) и импульсной функции (t) . Для

С помощью выражений (10) найдем изображение Лапласа для функции

(t) :

Данный результат также можно получить с помощью выражения (11):

Функцию (t) удобно использовать для задания начальных условий сис-

темы с помощью входного воздействия. Например, для двух способов пред-

47

ставления системы:

y ay , y(0) y0 ;

y ay y0 (t) , y(0) 0 ,

получим одно и тоже изображение Лапласа

Y ( p) y0 . p a

Такой способ задания начальных условий позволяет рассматривать сис-

темы при нулевых начальных условиях и при необходимости задавать их с по-

мощью (t) функций через входные воздействия.

3) Гармонический сигнал, определяемый по формуле u(t) um cos t или

u(t) um sin t , используется для имитации периодических воздействий, а так-

Для облегчения определения оригинала y(t) изображение Y ( p) с помо-

щью теоремы разложения [1] можно представить в виде суммы элементарных изображений, для которых по таблицам изображений определяются соответст-

вующие оригиналы и затем складываются.

48

3. Временные характеристики.

Реакция выхода y(t) при нулевых начальных условиях, построенная для входного сигнала 1(t) или (t) с помощью выражения (2.14), называется вре-

менной функцией, а ее график – временной характеристикой.

В зависимости от вида входного воздействия временные характеристики делятся на переходную характеристику и весовую характеристику. Рассмот-

рим их свойства.

3.1. Переходная характеристика

Определение 1. Реакция выхода системы y(t) на единичный скачок 1(t)

при нулевых начальных условиях называется переходной функцией, кото-

рая обозначается символом h(t) .

Учитывая, что для единичного скачка U ( p) 1/ p , переходная функция

50

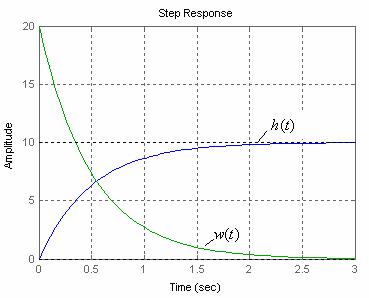
Решение аналогичной задачи для передаточных функций W ( p) общего вида можно проводить с помощью вычислительного пакета MATLAB [13]. При этом для построения характеристики h(t) используется команда step, а для построения весовой характеристики команда impulse. С помощью фрагмента программы для принятых значений параметров k 10, T 0,5 :

k=10;T=0.5;W=tf(k,[T 1]);step(W);hold on; impulse(W);grid

на рис. 3 приведены графики указанных характеристик.

Рис. 3

4. Частотные характеристики.

Частотные характеристики строятся по установившейся реакции системы на входной гармонический сигнал.

Пусть линейная система имеет один вход и один выход и записывается дифференциальным уравнением

a0 y(n) (t) a1y(n 1) (t) an y(t)

(20)

b0u(m) (t) b1u(m 1) (t) bmu(t),

которому при нулевых начальных условиях соответствует уравнение в изобра-

жениях Лапласа

с передаточной функцией