
Конспект лекц ТАУ _1ч _11 л
.pdf91
epittlij 1 /(lij 1)!
3. Переход от сигналов вход-выход к переменным состояния
Для определения реакции системы, заданной в виде передаточной матрицы
Y ( p) W ( p)U ( p), (17)
кроме способа обратного преобразования Лапласа можно использовать форму-
лу (6) при x(0) 0 , если установить связь между системами (17) и (1).
Рассмотрим этот вопрос для случая одномерных систем, полагая l m 1.
|
m( p) |
|
b pm |
b pm 1 |
b |
|
||||
W ( p) |
|
|
|
0 |
|
1 |
|
m |
, |
a 1. |
|
|
|
|
|
|
|
||||
|
d( p) |
|
a0 pn a1 pn 1 |
an |
0 |
|||||
|
|
|
||||||||
Уравнение (17) перепишем в виде |
|
|
|
|||||||
|
|
|
Y ( p) |
|
U ( p) |
Z( p) , |
|
|||
|
|
|
|
|
|
|||||
|
|
|
m( p) |
d( p) |
|
|
|
|||
где Z( p) – вспомогательная переменная. Тогда можно записать
d( p)Z( p) U ( p),
(18)
Y ( p) m( p)Z( p).
Системе (18) соответствует дифференциальное уравнение n - го порядка
z(n) (t) a1z(n 1) (t) anz(t) u(t),
(19)
y(t) b0z(m) (t) b1z(m 1) (t) bm z(t).
Введем вспомогательные переменные x1 z , |
x2 z x1 , |
|
xn z(n 1) |
xn 1, тогда уравнение (19) преобразуется к виду |
|
|
xn (t) a1xn (t) an x1(t) u(t), |
|
|
y(t) b0xm 1(t) b1xm (t) bm x1(t). |
|
Отсюда следует система уравнений
x1 x2,
x2 x3,
xn (t) anx1(t) an 1x2(t) a1xn (t) u(t), y(t) bmx1(t) bm 1x2 (t) b0xm 1(t).
x3 z x2 ,
(20)
92
Данную систему уравнений при m n перепишем в матричной форме (1),
где |
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
1 |
0 |
|
0 |
|
0 |
|
|
|
|
|
|
0 |
0 |
1 |
|
0 |
|
|
c b |
|
|
, |
|
A |
|
, |
b 0 , |
b |
b |
d 0 . |
||||||
|
|
1 |
0 |
m |
m 1 |
0 |
|
|
||||
|
|
an 1 |
an 2 |
|
|
|
|
|
|
|
|
|
an |
a1 |
1 |
|
|
|
|
|
|||||
Следует обратить внимание на то, что коэффициенты в последней строке матрицы A соответствуют коэффициентам полинома знаменателя передаточ-
ной функции W ( p) и согласно (3) соответствуют коэффициентам ее характери-
стического уравнения.
В случае, когда m n , выход системы y будет зависеть от координаты
xn 1 xn , после подстановки выражения которой получим другие выражения для вектора-строки c и скаляра d :
c bn b0an bn 1 b0an 1 b1 b0a1 , d b0 .
Существуют также другие формы представления системы (1) при выборе иного вектора состояния x [7]. Однако при этом передаточная функция (матри-
ца) остается одной и той же. Действительно, в результате подстановки x M x
в уравнение (1) и умножения слева на обратную матрицу M 1 получим
x M 1AM x M 1Bu, y CM x D.
Передаточная функция данной системы в соответствии с формулой (5) будет иметь вид
W ( p) CM pEn M 1AM 1 M 1B D CM M 1 pEn A M 1 M 1B D
CMM 1 pEn A 1 M M 1B D C pEn A 1 B D W ( p) .
Поэтому говорят, что передаточная функция системы (1) инвариантна к преобразованию подобия вектора состояния x .
Таким образом, исходная линейная система может быть представлена од-
ним из способов (1) или (17). При этом следует отметить, что кратным корням

93
характеристического уравнения d( p) 0 системы (17) или (20) соответствует
один жордановый блок, т.е. ri 1, ni li1 .
4. Блочные системы в переменных состояний
Для описания ФЭ вместо передаточных функций можно использовать представление в виде системы (1):
xi |
Ai xi biui , |
y |
cT x , |
i |
i i |
где xi ni - вектор состояния i - го ФЭ.
1. Последовательное соединение. При последовательном соединении двух
ФЭ u1 u u2 y1 , |
y y2 . Тогда с использованием расширенного вектора со- |
|||||||||||
стояния x [xT |
xT ]T |
размерностью n n n |
получим эквивалентную систему |
|||||||||
1 |
2 |
|
|
|
1 |
2 |
|
|
|
|
|
|
с блочными матрицами: |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
A1 |
0 |
|
b |
|
|
|||
|
|
x |
b cT |
x |
|
1 |
u, |
(21) |
||||
|
|
|
A |
|
0 |
|
||||||
|
|
|
2 1 |
2 |
|
|
|
|
|
|
|
|
|
|
y [0 |
c2T ]x. |
|
|
|
|
|
|
|
||
При последовательном соединении k |
ФЭ блочная матрица является ниж- |
|||||||||||
ней треугольной с диагональными блоками Ai , |
i |
|
. |
|
||||||||
1,k |
|
|||||||||||
2. Параллельное соединение. При параллельном соединении двух ФЭ |
||||||||||||
u1 u u2 u , y y1 |
y2 . Тогда получим эквивалентную систему: |
|
||||||||||
|
|
A |
0 |
b |
|
|
|
|
|
|||
|
|
x |
1 |
x |
|
1 |
u, |
(22) |
||||
|
|
|
0 |
A2 |
b2 |
|
|
|
||||
|
|
y [cT |
cT ]x. |
|
|
|
|
|
|
|
||
|
|
|
|
1 |
2 |
|
|
|
|
|
|
|
При параллельном соединении k ФЭ блочная матрица является диаго-
нальной с блоками Ai , i 1,k .
3. Соединение с обратной связью. При использовании второго ФЭ в каче-
стве обратной связи имеем u1 u y2 , u2 y1 , y y1. Тогда получим эквива-
лентную систему:
|
|
|
|
|
|
|
|
|
94 |
x |
|
A |
|
b cT |
b |
|
|
||
|
1 |
1 2 x |
1 |
u, |
(23) |
||||
|
b c |
T |
A |
|
|
0 |
|
||
|
|
2 1 |
2 |
|
|
|
|
|
|
y [cT |
0]x. |
|
|
|
|
|
|||
|
|
1 |
|
|
|
|
|
|
|
Возможны также и другие соединения блоков ФЭ.
В системе MATLAB предусмотрена возможность программно “набирать” схему САУ, состоящую из ФЭ в виде передаточных функций (матриц) и блоков в переменных состояний. Если с помощью команды tf ФЭ представлен в виде передаточной функции (матрицы) W, то для перехода к системе (1) можно вос-
пользоваться командой sys1=ss(W). Для обратного перехода используется команда sys2=tf(sys1). Выполнение разложения (13), т.е. вычисление мат-
риц M и J , можно осуществить с помощью команды [M,J]=jordan(A).
Для вычисления матричной экспоненты используется команда expm(A).
Также отметим, что в системе Simulink [8, 2] имеется возможность моде-
лирование САУ с помощью передаточных функций и матричных блоков.
Вопросы для самопроверки
1.Что понимается под переменными состояния?
2.В чем преимущество и недостаток систем в переменных состояния по срав-
нению с их представлением передаточными матрицами?
3.Какие известны способы построения переходной матрицы?
4.Что понимается под свободным и вынужденным движением системы?
5.В чем особенность представления матрицы в форме Жордана?
6.От чего зависит решение однородной системы линейных дифференциальных уравнений?
7.Что понимается под инвариантностью передаточной функции к подобному преобразованию?
8.Отличаются ли корни характеристического уравнения системы при последо-
вательном и параллельном соединении блоков ФЭ?
95
ЛЕКЦИЯ 8
Устойчивость САУ. Определение устойчивости по Ляпунову. Устойчивость линей-
ных систем. Теоремы Ляпунова об устойчивости по линейному приближению.
1. Устойчивость САУ
Рассматриваются два подхода к определению устойчивости САУ.
1) Пусть заданное или невозмущенное движение системы описывается уравнением
x*(t) F(x*(t),u*(t)) , x*(t |
0 |
) x* , |
(1) |
|
|
|
0 |
|
|
где x* n- вектор состояния, |
u* m- вектор управляющих воздействий, |
F( ) – |
||
нелинейная вектор-функция, удовлетворяющая условиям существование и единственности решения системы (1).
Предположим, что в момент времени t t0 из-за внешних возмущений изменилось начальное условие, которое приняло значение x0 x0* x0 . При
этом возмущенное движение системы при t t0 отклоняется от невозмущенно-
го движения x*(t) и описывается уравнением
x(t) F(x(t), u*(t)) , x |
x* x . |
(2) |
|
0 |
0 |
0 |
|
Очевидно, что для нормальной работы системы необходимо, чтобы после
снятия возмущающих воздействий возмущенное движение системы стремилось к невозмущенному движению при t . Данное свойство системы называют
устойчивостью системы или устойчивостью невозмущенного движения.
В частном случае, если x*(t) 0 , система (1) при u*(t) const находится в
состоянии равновесия x*(t) x*(t0 ), которое определяется из уравнения стати-
ки
F(x*,u*) 0. |
(3) |
В силу нелинейности уравнения (2) может существовать множество состояний равновесия. При этом каждое положение равновесия может быть устойчивым,
96
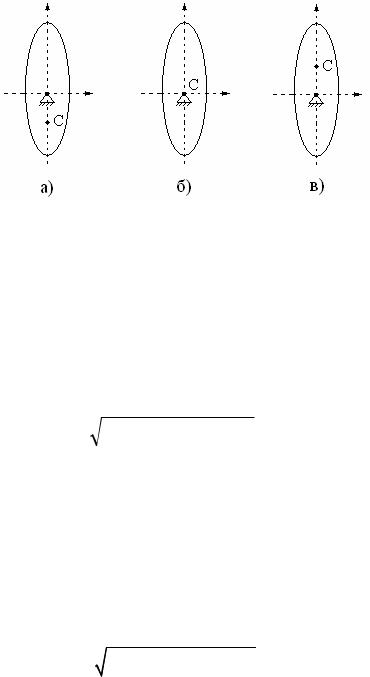
нейтральным и неустойчивым. Примером может служить движение физическо-
го маятника при наличии сил трения, представленного на рис. 1. В зависимости от положения точки С центра масс маятника его положение равновесия являет-
ся устойчивым (а), нейтральным (б), неустойчивым (в).
Рис. 1
2) Другое определение устойчивости связано с реакцией системы на из-
менение управляющего воздействия u* . Пусть в момент времени t t0 управ-
ляющее воздействие приняло значение u(t) u*(t) u(t) , где u(t) – произ-
вольное ограниченное воздействие, удовлетворяющее условию
|| u(t) || 
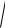 u12 (t) um2 (t) umax .
u12 (t) um2 (t) umax .
При этом возмущенное движение системы, отклоняющееся от невозмущенного движения x*(t), описывается уравнением
x(t) F(x(t), u*(t) u(t)) , x(t |
) x . |
(4) |
||||||
|
|
|
|
0 |
|
0 |
|
|
Если отклонение x(t) x(t) x*(t) при t |
0 |
t является ограниченным, т.е. |
||||||
|
|
|
|
|
|
|
|
|
выполняется условие |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|| x(t) || |
x2 (t) x2 |
(t) x |
, |
(5) |
||||
|
1 |
|
m |
|
|
max |
|
|
то система (1) называется устойчивой по входу.
Устойчивость по входу связана с понятием устойчивости невозмущенно-
го движения.
97
2. Определение устойчивости по Ляпунову
Рассмотрим первый подход к определению устойчивости невозмущенно-
го движения системы (1), полагая u*(t) известным вектором. Для этого запи-
шем уравнение (2) в отклонениях от невозмущенного движения системы (1)
полагая x(t) x*(t) x(t) . Тогда вычитая из уравнения (2) уравнение (1) полу-
чим
x(t) F(x*(t) x(t), u*(t)) F(x*(t),u*(t)) f ( x(t), t) .
Таким образом, возмущенное движение системы в отклонениях от невоз-
мущенного движения описывается нестационарной системой
x(t) f ( x(t), t) , |
x(t |
) x(t |
0 |
) x*(t |
0 |
) , |
(6) |
|
0 |
|
|
|
|
где f ( x(t), t) f (0, t) 0. При этом для системы (6) невозмущенным движени-
ем является решение x(t) 0.
Определение 1. Невозмущенное движение x*(t) системы (1) (или x(t) 0
системы (6)) называется устойчивым по Ляпунову, если для любого сколь угод-
но малого 0 найдется ( ) 0 такое, что при начальных условиях
|| x(t0 ) || || x(t0 ) x*(t0 ) ||
выполняется неравенство || x(t) || || x(t) x*(t) || при t t0 .
В противном случае невозмущенное движение называется неустойчивым по Ляпунову.
Определение 2. Если исходная система (1) (или (6)) устойчива по Ляпуно-
ву и выполняется также условие lim x(t) 0 , то невозмущенное движение
t
x*(t) системы (1) (или x(t) 0 системы (6)) асимптотически устойчиво.
Если исходная система асимптотически устойчива для любых начальных отклонений, то невозмущенное движение устойчиво в целом.
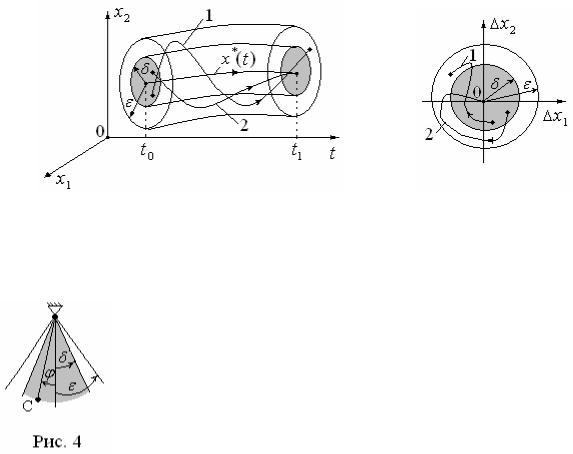
Приведем геометрическую интерпретацию определения устойчивости по Ляпунову для случая n 2. На рис. 2 невозмущенное движение x*(t) является осью трубки с внутренним и внешним радиусами. При этом возмущенное
98
движение x(t) , соответствующее кривой 1, является устойчивым по Ляпунову,
а кривой 2 – асимптотически устойчивым. На рис. 3 приведены соответствую-
щие возмущенные движения x(t) в отклонениях от невозмущенного x(t) 0.
Рис. 2 Рис. 3
Примером устойчивой системы по Ляпунову является математический маятник, приведенный на рис. 4. Здесь начальное угловое поло-
жение маятника | (t0 ) | . Поэтому при свободных колебаниях маятника будет выполняться условие | (t) | , т.е. движе-
ние маятника устойчиво по Ляпунову. Если движению маятника препятствует сопротивление среды, то его колебания будут за-
тухающими и тем самым движение является асимптотически устойчивым. |
|
|||||
В дальнейшем будем рассматривать систему (6) при u*(t) const |
в от- |
|||||
клонениях от невозмущенного движения, опуская для простоты символ : |
|
|||||
x f (x), x(t0 ) x0 , |
(7) |
|||||
где f (0) 0. Разлагая функции fi (x) , i |
|
|
в ряд Тейлора, получим |
|
||
1,n |
|
|||||
n |
fi (x) |
|
|
|
|
|
|
|
|
|
|||
fi (x) |
|
|
x j i (x), |
|
||
xj |
|
|
|
|||
j 1 |
|
x 0 |
|
|||
|
|
|
|
|
||
где i (x) – слагаемые содержащие члены выше первого порядка малости. Тогда уравнение (7) можно переписать в виде:
x Ax (x) , x(t0 ) x0 , (8)
где постоянная матрица A определяется по формуле
|
|
|
|
|
|
|
|
|
|
|
|
99 |
|
|
|
|
|
f1(x) |
|
|
f1(x) |
|
|||
|
|
|
|
|
|
x |
|
|
|
x |
|
|
A |
f (x) |
|
|
|
1 |
|
|
|
n |
|
||
|
|
|
||||||||||
|
|
|
|
. |
||||||||
x |
|
|
||||||||||
|
|
x 0 |
|
fn (x) |
|
fn (x) |
|
|||||
|
|
|
||||||||||
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
x |
|
|
x |
|
||
|
|
|
|
|
1 |
|
|
|
n |
x 0 |
||
3. Устойчивость линейных систем |
|
|
|
|
||||||||
При малых отклонениях вектора x |
функцией (x) можно пренебречь и |
|||||||||||
тогда из системы (8) следует линейная система: |
|
|
|
|
||||||||
|
|
|
x Ax , x(t0 ) x0 . |
(9) |
||||||||
Следует отметить, что возможны случаи, |
|
когда в системе (8) функция |
||||||||||
(x) 0 , т.е. система является линейной, при этом отклонении вектора x могут быть произвольными.
Для определения устойчивости системы (9) по Ляпунову необходимо
проанализировать поведение нормы вектора || x(t) || , где решение x(t) при
t0 0 в случае различных корней определяется по формуле (7.16) и удовлетво-
ряет неравенству
n |
|
|
|| x(t) || | epit |
| || ci ||. |
(10) |
i 1 |
|
|
Здесь комплексному корню pi соответствует комплексный вектор ci , норма ко-
торого равна корню квадратному из суммы квадратов модулей координат век-
тора ci . |
|
|
|
|
Таким образом, поведение нормы вектора |
|| x(t) || зависит от функций |
|||
| epit |, и в случае кратных корней p |
– может зависеть от функций | epit |, | epitt |, |
|||
|
i |
|
|
|
…, | epittk |. |
|
|
|
|
Рассмотрим различные случаи распределения корней |
pi i j i харак- |
|||
теристического уравнения |
|
|
|
|
d( p) | pE |
A | pn a pn 1 a 0 |
(11) |
||
n |
|
1 |
n |
|
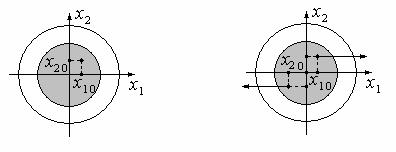
на комплексной плоскости, которым соответствует выражение
100
epit e( i j i )t e ite j it .
Отсюда с учетом равенства | e j it | | cos it jsin it | 1 получим
| epit | | e it | | e j it | | e it | .
1. Корни с отрицательной вещественной частью. |
При значении i |
0 |
||
функция e it 0 , поэтому функция | epit | 0 . |
|
|
||
t |
t |
|
|
|
Несложно также показать, что функция | epittk | 0 |
для любого конечно- |
|||
|
|
t |
|
|
го значения k . |
|
|
|
|
2. Корни с положительной вещественной частью. |
При значении i |
0 |
||
функция e it и, следовательно, функция | epit | . |
|
|
||
t |
|
t |
|
|
3. Корни с нулевой вещественной частью. При значении i 0 функция |
||||
e0t 1, и, следовательно, | epit | 1. При этом функция | epittk | . |
|
|||
|
|
|
t |
|
|
|
0 |
0 |
|
Пример 1. Пусть система (9) имеет матрицу A |
. Характеристиче- |
|||
ское уравнение |
|
0 |
0 |
|
p |
0 p2 0 , |
|
|
|
d( p) | pE A | |
|
|
||
n |
|
|
|
|
|
0 |
p |
|
|
имеет кратные корни p1,2 0 . Тогда решение x(t) можно записать с помощью формулы (7.9) в виде
x(t) E2x(t0 ) x(t0 ) ,
т.е. x1(t) x1(t0 ) , x2(t) x2(t0 ) (рис. 5).
Таким образом, система устойчивая по Ляпунову.
Рис. 5 Рис. 6
