5.2.3. Разыгрывание дискретной случайной величины

Допустим, что нужно имитировать значения дискретной случайной величины с распределением

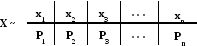
Построим на оси интервалы длинами: P₁,P₁ + P₂, P₁ + P₂ + P₃, …, P₁ + P₂ + … + P_n. Выберем из таблицы случайных чисел цифру R_j умножим ее на 0,1. Пусть R_j попало в j-й интервал. Можно показать, что вероятность

P { P₁ + P₂ + … + P_j-1 < R_j < P₁ + P₂ + … + P_j} = P_j,

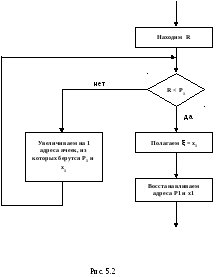
поскольку случайная величина R распределена равномерно. В этом случае разыгрываемая величина X равна х_j. На рис. 5.2 пока­зано, как реализовать получение произвольного числа значений Х на ЭВМ.

5.2.4. Разыгрывание непрерывной случайной величин

Допустим, что требуется получать значения непрерывной случайной величины X, распределенной в интервале (a, b) с плотностью f(х) произвольного вида.

Можно показать, что значение х_i в i-м испытании (разыгрывании) определяется по формуле

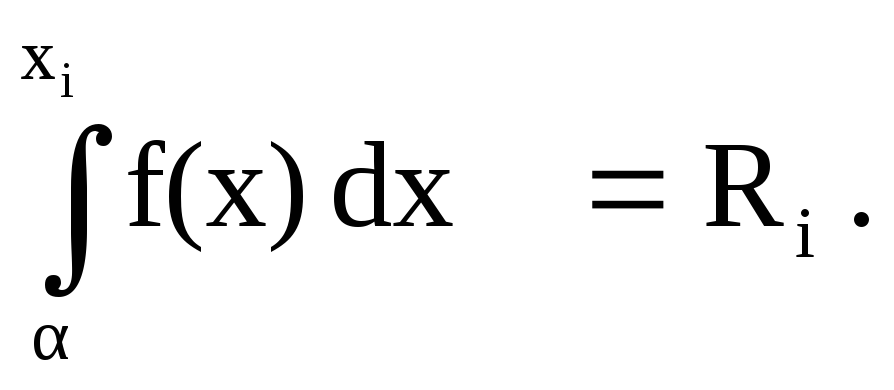(5.2)

Таким образом, выбрав очередное значение R_j, необходимо решить уравнение (5.2) и найти х_j. На рис. 5.3 иллюстрируется графическое решение этого уравнения, где кривая представляет плотность распределения х.

Рассмотрим характерные примеры. Разыгрывание наработки на отказ, представляющей случайную величину t, распределенную экспоненциально. Плотность распределения t имеет вид . Формулу для разыгрывания t легко получить на основании зависимости (5.2):

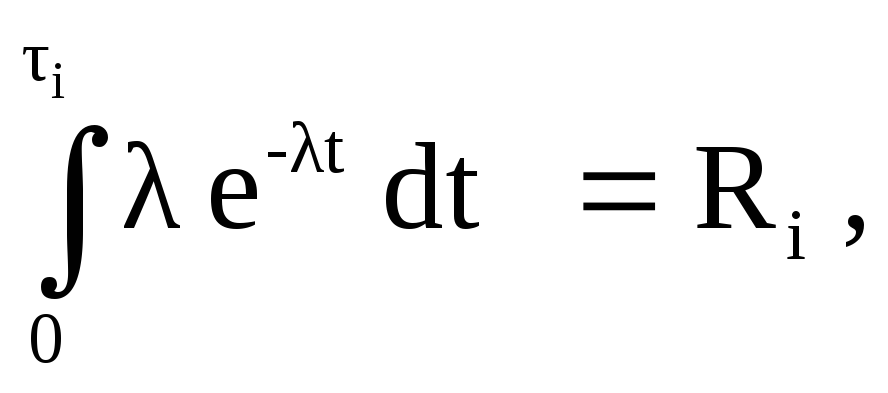
где i - i-e испытание (разыгрывание).

Вычислив интеграл, получим

откуда

(5.3)

Поскольку случайная величина (1 – R_i) распределена точно так же, как R_i, то

(5.4)

Разыгрывание нормально распределенной случайной величины х затруднено, поскольку уравнение

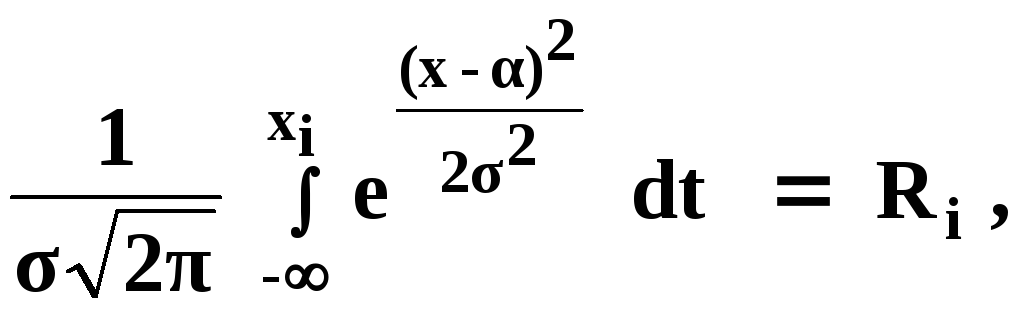(5.5)

где α, s - математическое ожидание и среднее квадратическое отклонение, в явном виде неразрешимо и интервал возможных значений х бесконечен. В этой связи пользуются приближенным решением уравнения (5.5), имеющим вид

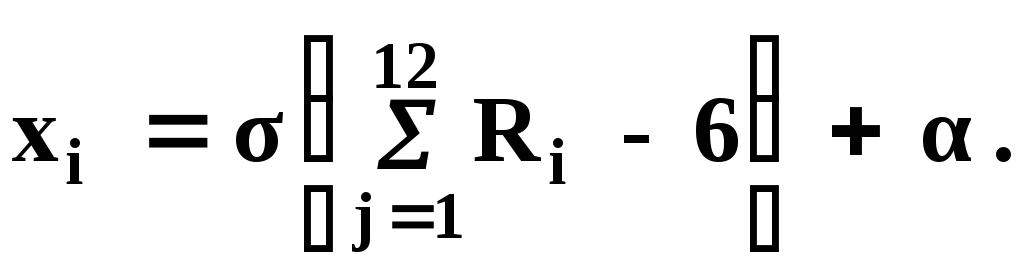(5.6)

Как видно из (5.6), необходимо выбирать 12 значений случайной величины R, чтобы определить одно значение случайной величины с нормальным распределением. Имеются и другие зависимости для ее имитации.

5.2.5. Определение необходимого числа реализации в имитационном эксперименте

Поскольку в результате применения МСИ получают выборку значений представляющего случайную величину показателя надежности, то при построении имитационной модели возникает важный вопрос о правомерности распространения информации о выборочных характеристиках на истинные характеристики указанной случайной величины. Ясно, что чем большее число испытаний N включается в имитационный эксперимент, то есть чем больше объём выборки, тем точнее выборочное математическое ожидание, среднее квадратическое отклонение и другие характеристики. Однако увеличение N ведет к потерям дорогостоящего машинного времени. В этой связи N стремятся выбрать как можно меньшим при условии, что обеспечивается необходимая близость между выборочными и истинными характеристиками показателя надёжности. Применительно к математическому ожиданию того или иного показателя надёжности вопрос о точности МСИ решается на основе центральной предельной теоремы теории вероятностей следующим образом.

Пусть - заданная погрешность, где- выборочное, α - истинное математическое ожидание представляющего случайную величину параметра надёжности. Зададимся достаточно близкой к 1 вероятностью Р и решим вопрос о том, каким должно быть число реализации N, чтобы с вероятностью Р погрешность в определении α не превышалаe. Понятно, что рассмотрение этого вопроса без учета сходимости к α по вероятности некорректно, посколькуявляется случайной величиной. сходящейся в вероятностном смысле к α при неограничен­ном увеличении N.

Поставленный вопрос решается с использованием конкретизирующего центральную предельную теорему неравенства

(5.7)

где Ф(Z) - табулированная функция Лапласа, Z - ее аргумент. Из этого выражения найдем, что

и по таблице Ф(Z) определим Z. Так как с вероятностью Р согласно выражению (5.7) должно быть , то

Следовательно, можно положить, что

(5.8)

Поскольку заранее неизвестно, определение N осуществляется итеративно: задают, например,N₁ = 100. После осуществления 100 реализации находят и с его использованием -. На основании (5.8) по заданному значениюe, известным Z и проверяют, достаточно ли числа испытанийN₁. Если достаточно, то полагают N = N₁. В противном случае увеличивают N₁, например, на 50 и снова осуществляют расчет ,и проверку достаточности испытаний. Расчёты проводятся на ЭВМ по соответствующей программе