
- •Государственное образовательное учреждение высшего профессионального образования «Ростовский военный институт ракетных войск Министерства обороны Российской Федерации»
- •Надежность систем и средств управления
- •Введение
- •1. Количественные показатели надежности автоматизированных систем
- •1.1. Проблема надежности в технике
- •1.2. Основные понятия и определения теории надежности
- •1.3. Показатели надежности невосстанавливаемых систем
- •1.3.1. Вероятность безотказной работы Вероятностное определение
- •Статистическое определение
- •1.3.2. Плотность распределения отказов
- •Статистическое определение
- •1.3.4. Средняя наработка до отказа Вероятностное определение
- •Статистическое определение
- •1.4. Законы распределения наработки технического объекта до отказа и между отказами
- •Вопросы для самоконтроля
- •2. Надежность невосстанавливаемых систем
- •2.1. Задание требований по надёжности
- •2.2. Виды расчетов надежности невосстанавливаемых нерезервированных систем
- •2.2.1. Прикидочный расчет надежности
- •2.2.2. Расчет надёжности при подборе типов элементов
- •2.2.3. Расчет надёжности при уточнении режимов работы элементов
- •2.3. Структурные схемы надёжности технических объектов. Резервирование, его виды и способы
- •2.4. Расчет надёжности при различных способах структурного резервирования
- •2.4.1. Определение показателей надежности при постоянном общем резервировании
- •2.4.2. Определение показателей надежности при постоянном раздельном резервировании
- •2.4.3. Сравнительная оценка раздельного и общего постоянного резервирования
- •Тобщ £ max (t1,t/1) .
- •Тобщ £ max (t2,t/2) .
- •2.4.4. Определение показателей надежности при резервировании замещением
- •Вопросы для самоконтроля
- •3. Надежность восстанавливаемых систем
- •3.1 Потоки отказов и восстановлений
- •3.2 Количественные показатели надежности восстанавливаемых систем
- •3.2.1 Показатели безотказности
- •3.2.2 Показатели ремонтопригодности
- •3.2.3 Комплексные показатели
- •3.3. Расчет надежности восстанавливаемых нерезервированных систем
- •3.4. Расчет надежности восстанавливаемых резервированных систем
- •3.5. Способы поддержания заданного уровня надёжности
- •3.5.1. Факторы, влияющие на надежность
- •3.5.2.Способы повышения надёжности систем на этапе проектирования и их сравнительный анализ
- •3.5.3. Способы поддержания заданного уровня надёжности и готовности систем
- •Вопросы для самоконтроля
- •4. Оценка надежности дискретных устройств с восстанавливающими органами
- •4.1. Особенности отказов в дискретных устройствах ссу
- •4.2. Восстанавливающие органы дискретных устройств
- •4.2.1. Основные определения
- •4.2.2. Коррекция ошибок (отказов) типа ложный "0".
- •4.2.3. Коррекция ошибок (отказов) типа ложная "1"
- •4.2.4. Структурные схемы восстанавливающих органов
- •Восстанавливающий орган
- •Восстанавливающий орган
- •Восстанавливающий орган
- •4.3. Оценка надёжности дискретных устройств с во
- •4.3.1. Определение вероятности возникновения на выходе во отказа по "0"
- •4.3.2. Определение вероятности возникновения на выходе во отказа по "1"
- •4.3.3. Определение вероятности безотказной работы
- •Вопросы для самоконтроля
- •5. Применение метода статистических испытаний для анализа надёжности сложных систем
- •5.1. Определение статистических значений показателей надежности систем по данным испытаний на надёжность и по статистическим данным о надёжности
- •5.2. Применение метода статистических испытаний для анализа надёжности сложных систем
- •5.2.1. Метод статистических испытаний
- •5.2.2. Сущность мси и реализации на эвм случайного эксперимента
- •5.2.3. Разыгрывание дискретной случайной величины
- •5.2.4. Разыгрывание непрерывной случайной величин
- •5.2.5. Определение необходимого числа реализации в имитационном эксперименте
- •5.3. Типовые моделирующие алгоритмы
- •Вопросы для самоконтроля
- •Заключение
- •Библиографический список
- •Надежность систем и средств управления
3.2 Количественные показатели надежности восстанавливаемых систем
3.2.1 Показатели безотказности
В
пределах любого i – го
отдельного интервала безотказной работы
(рис. 3.1) для восстанавливаемых систем
(объектов) справедливы все показатели
безотказности, рассмотренные для
невосстанавливаемых систем: P(t),
Q(t),
f(t),
![]() (t),
To,
если считать за начальный момент времени
t
= 0 начало i – го
интервала безотказной работы.
(t),
To,
если считать за начальный момент времени
t
= 0 начало i – го
интервала безотказной работы.
Кроме этих показателей безотказности, используются и дополнительные показатели безотказности, учитывающие процессы отказов и восстановлений, характерные именно для восстанавливаемых систем:
1. Параметр потока отказов (t)– отношение среднего числа отказов восстанавливаемого объекта за произвольно малую его наработку к значению этой наработки:
![]() ,
(3.1)
,
(3.1)
где
![]() ,
,
![]() – математическое ожидание числа отказов
n
за время t +
– математическое ожидание числа отказов
n
за время t + ![]() t
и t
соответственно.
t
и t
соответственно.
Для
стационарного потока отказов
![]() является величиной постоянной, т.е.
является величиной постоянной, т.е.
![]() .
Из (3.1) имеем:
.
Из (3.1) имеем:
![]() .
.
Статистически параметр потока отказов определяется по формуле:
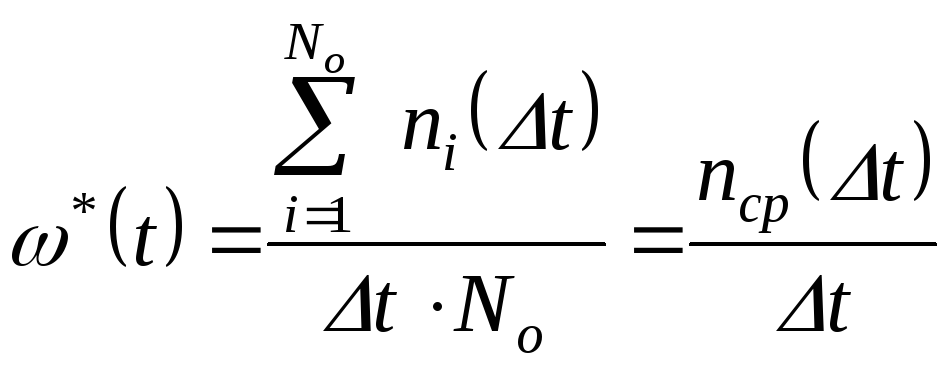 ,
(3.2)
,
(3.2)
где ![]() – суммарное
число отказов i – го
испытуемого образца на интервале времени
– суммарное
число отказов i – го
испытуемого образца на интервале времени
![]() (от
t
до t
+
(от
t
до t
+
![]() );
);
![]() – суммарное
число отказов, возникших во всех
– суммарное
число отказов, возникших во всех
![]() объектах на интервале времени
объектах на интервале времени![]() ;
;
![]() – среднее
число отказов на интервале
– среднее
число отказов на интервале
![]() ,
приходящееся на один испытуемый объект:
,
приходящееся на один испытуемый объект:
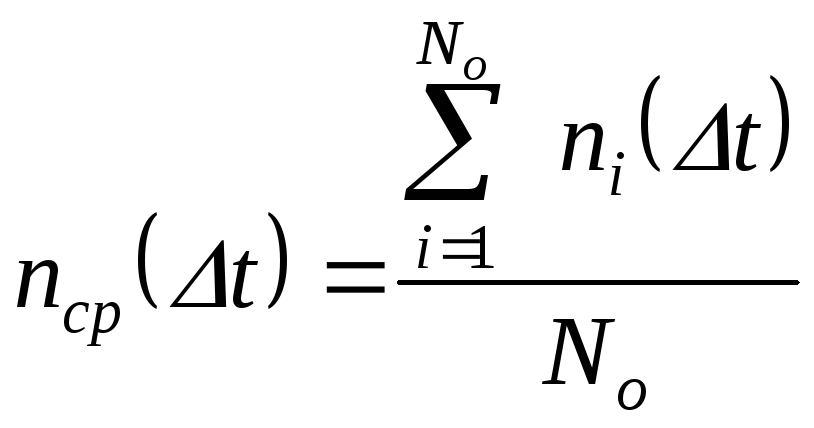 (3.3)
(3.3)
2. Средняя наработка на отказ Тср (Тср= Тр.ср) – отношение наработки восстанавливаемого объекта к среднему числу его отказов в течение этой наработки:
![]() (3.4)
(3.4)
или для статистического значения
![]() (3.5)
(3.5)
Этот показатель характеризует среднее время безотказной работы между двумя соседними отказами (i – 1) – м и i – м восстанавливаемого объекта.
Для
простейшего потока отказов (ординарного,
без последействия, стационарного)
![]() и получим:
и получим:
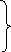
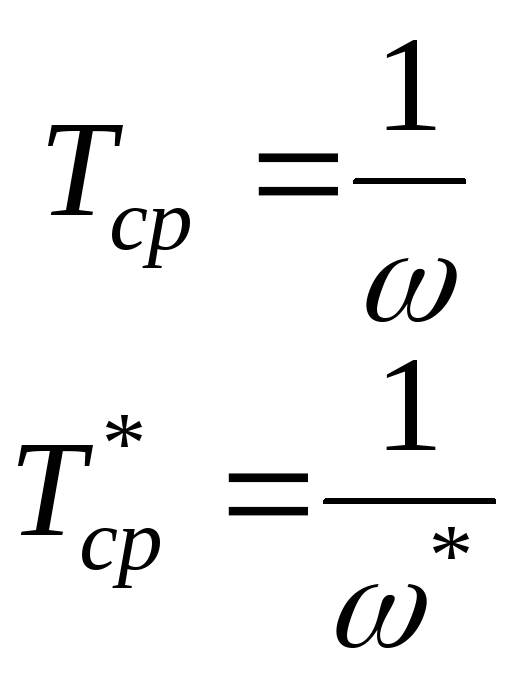 (3.6)
(3.6)
 ,
,
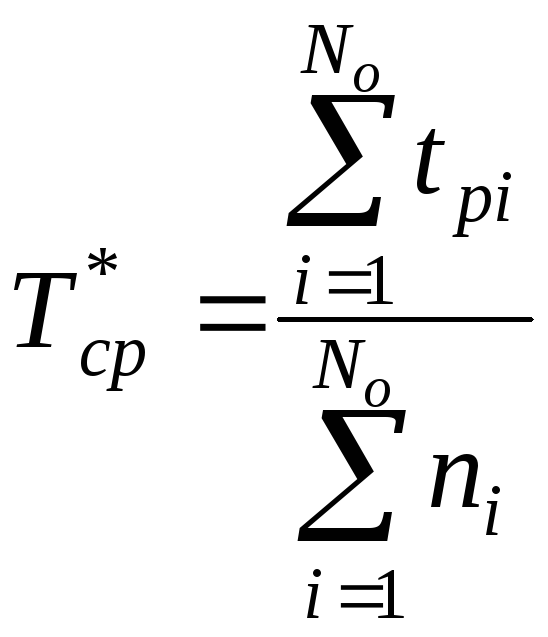 ,
(3.7)
,
(3.7)
где ![]() – суммарное
время безотказной работы i – го
образца;
– суммарное
время безотказной работы i – го
образца;
![]() – суммарное
число отказов i – го
образца за время испытаний.
– суммарное
число отказов i – го
образца за время испытаний.
3. Вероятность возникновения (появления) некоторого числа n отказов на интервале времени (0, t) определяется формулой закона Пуассона (для простейшего потока):
![]() ,
,
![]() ,
,
![]() .
(3.8)
.
(3.8)
При числе отказов n = 0 формула (3.8) примет вид:
![]()
и будет определять вероятность безотказной работы восстанавливаемой системы за время t.
3.2.2 Показатели ремонтопригодности
1. Вероятность
восстановления работоспособного
состояния
![]() – вероятность того, что время восстановления
работоспособного состояния объекта
– вероятность того, что время восстановления
работоспособного состояния объекта
![]() не превысит заданного времени t
(рис. 3.4):
не превысит заданного времени t
(рис. 3.4):
![]() ,
(3.9)
,
(3.9)
Рис. 3.4
Функция
![]() представляет собой интегральную функцию
распределения случайной величины
представляет собой интегральную функцию
распределения случайной величины
![]() .
С вероятностной
точки зрения она идентична рассмотренной
ранее функции Q(t)
(вероятности отказа) и имеет такие же
свойства.
.
С вероятностной
точки зрения она идентична рассмотренной
ранее функции Q(t)
(вероятности отказа) и имеет такие же
свойства.
Статистически
вероятность
![]() определяется по формуле:
определяется по формуле:
![]() ,
(3.10)
,
(3.10)
где ![]() – число
объектов, восстановленных за время t;
– число
объектов, восстановленных за время t;
![]() – число
объектов, поставленных на восстановление.
– число
объектов, поставленных на восстановление.
2. Плотность
вероятности восстановления работоспособного
состояния объекта (частота восстановления,
плотность (закон) распределения времени
восстановления
![]() )
)
![]() – дифференциальная функция распределения
случайной величины
– дифференциальная функция распределения
случайной величины
![]() ,
определяется через производную от
интегральной функции:
,
определяется через производную от
интегральной функции:
![]() ,
(3.11)
,
(3.11)
где μ – интенсивность восстановления работоспособного состояния объекта.
Установим
связь вероятности
![]() с характеристиками
с характеристиками![]() иμ.
Запишем уравнение (3.11) в виде
иμ.
Запишем уравнение (3.11) в виде
![]() и, после интегрирования обеих частей,
получим:
и, после интегрирования обеих частей,
получим:
![]() ,
,
![]() .
(3.12)
.
(3.12)
Вероятность
![]() является возрастающей экспонентой.
является возрастающей экспонентой.
Статистическая
оценка показателя
![]() :
:
![]() ,
(3.13)
,
(3.13)
где
![]() – число объектов, восстановленных в
интервале времени
– число объектов, восстановленных в
интервале времени![]() t.
t.
3. Интенсивность
восстановления объекта за время
![]() μ(t)
– условная
плотность вероятности восстановления
объекта в момент времени t
при условии, что до этого момента времени
t
восстановления объекта не произошло:
μ(t)
– условная
плотность вероятности восстановления
объекта в момент времени t
при условии, что до этого момента времени
t
восстановления объекта не произошло:
![]() .
.
Для экспоненциального закона восстановления (3.12) характеристика μ(t) является постоянной μ(t) = μ в течении времени нормальной эксплуатации и ее точное значение равно:
![]() ,
(3.14)
,
(3.14)
где ![]() – среднее время восстановления объекта.
– среднее время восстановления объекта.
Статистически интенсивность восстановления равна:
![]() ,
(3.15)
,
(3.15)
где ![]() – число не восстановленных объектов
за времяt.
– число не восстановленных объектов
за времяt.
4.
Среднее время восстановления
![]() – математическое ожидание времени
восстановления работоспособного
состояния объекта (математическое
ожидание случайной величины
– математическое ожидание времени
восстановления работоспособного
состояния объекта (математическое
ожидание случайной величины![]() ).
).
Т.к.
случайная величина
![]() является непрерывной, то
является непрерывной, то
![]() .
(3.16)
.
(3.16)
Приведем
интеграл (3.16) к табличному виду
![]() ,
для чего введем следующие обозначенияt
= u,
,
для чего введем следующие обозначенияt
= u,
![]() ,
,![]() ,
,![]() .
После подстановки значений в (3.16),
получим:
.
После подстановки значений в (3.16),
получим:
![]() .
(3.17)
.
(3.17)
В
выражении (3.17) произведение
![]() при
при![]() будет равно единице, так как при
будет равно единице, так как при![]() вероятность
вероятность![]() будет стремиться к единице быстрее, чем
параметрt
будет стремиться к бесконечности и
будет стремиться к единице быстрее, чем
параметрt
будет стремиться к бесконечности и
![]() .
Подстановка нижнего пределаt
= 0 даст
.
Подстановка нижнего пределаt
= 0 даст
![]() .
.
Таким образом, окончательно получим:
![]() .
(3.18)
.
(3.18)
Определим связь между характеристиками Тв и μ.
Для
этого подставим в правую часть уравнения
(3.17) значение вероятности
![]() и получим:
и получим:
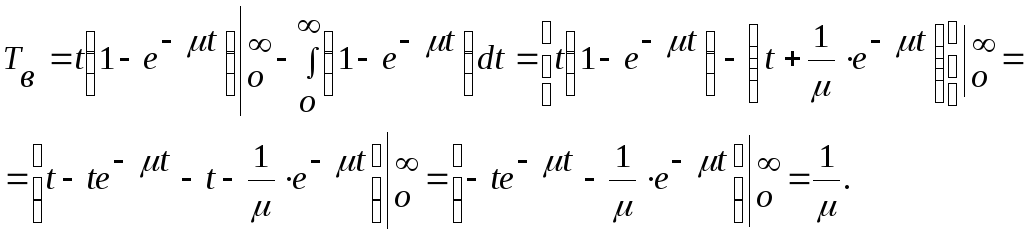
![]() .
(3.19)
.
(3.19)
Статистическая
оценка показателя
![]() :
:
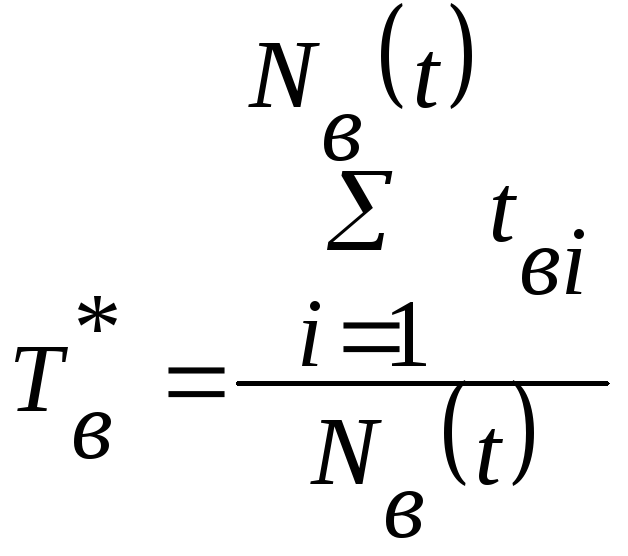 ,
(3.20)
,
(3.20)
где ![]() – суммарное
время, затраченное на восстановление
всех возникших
– суммарное
время, затраченное на восстановление
всех возникших![]() отказов уi – го
испытуемого объекта за время t;
отказов уi – го
испытуемого объекта за время t;
![]() – суммарное
время восстановления всех
– суммарное
время восстановления всех![]() образцов.
образцов.
Учитывая,
что для восстанавливаемых систем число
восстановлений равно числу отказов, и
каждый испытуемый объект за время
испытаний может иметь несколько отказов,
то характеристику
![]() (для удобства вычисления) можно определить
по следующей формуле:
(для удобства вычисления) можно определить
по следующей формуле:
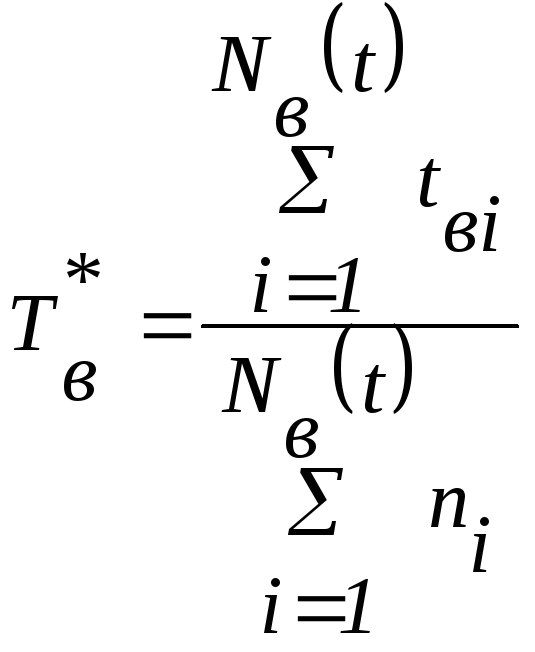 ,
(3.21)
,
(3.21)
где ![]() – суммарное
число отказов, возникших уi – го
объекта за время испытаний t.
– суммарное
число отказов, возникших уi – го
объекта за время испытаний t.
В
формуле (3.21) верхнее значение Nв(t)
в знаках суммирования можно заменить
числом Nо
, т.е. общим числом объектов, поставленных
на испытание. В этом случае для не
отказавших объектов соответствующие
значения
![]() и
и![]() будут равны 0. Тогда статистическая
оценка
будут равны 0. Тогда статистическая
оценка![]() будет иметь вид:
будет иметь вид:
 .
(3.22)
.
(3.22)
Выражения
(3.21) и (3.22) определяют характеристику
![]() как среднее время, затрачиваемое на
восстановление одного отказа в одном
объекте.
как среднее время, затрачиваемое на
восстановление одного отказа в одном
объекте.
