de1

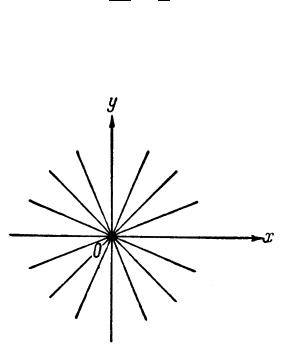
5b. Все коэффициенты системы (1.17.10) равны 0: a = d = 0, b = c = λ. Уравнение имеет простейший вид

dxdy = xy ,

его общее решение y = Cx. Это дикритический узел, показанный на рис. 6 (угловой коэффициент касательных может иметь всевозможные значения)

Рис. 6.

1.18.Понятие устойчивости

Исследование точек равновесия механической системы тесно связано с понятием устойчивости. Казалось бы, определение всех точек покоя дает нам исчерпывающую информацию о том, в каком состоянии может находиться система, но это далеко не так. Например, у обычного маятника имеется два положения равновесия, но реализуется только одно – “гирей маятника вниз”. Второе положение маятника является, как говорят физики, “ненаблюдаемым”. Здесь надо учитывать, что любая модель идеализирована, а на практике всегда существуют флюктуации – малые случайные возмущения. Всякое такое возмущение приводит к тому, что маятник покидает состояние равновесия “гирей маятника вверх” и стремится к единственному реализуемому. Аналогичные, но более сложные ситуации возникают в системе “Земля – Луна”, в системах кратных звезд, в кольцах астероидов и крупных планет (здесь на проблемы поведения системы в окрестностях точек покоя накладываются резонансные явления и соответствие или несоответствие системы пределу Роша).

Рассмотрим уравнение

61

Очевидно, одним из решений уравнения (1.18.1) является x ≡ 0, оно удовлетворяет начальному условию x(t0) = 0, для которого это решение является единственным. Назовем это решение невозмущенным, а всякое решение с ненулевым начальным условием будем называть возмущенным (x0 =6 0 – возмущение). Нас будет интересовать поведение возмущенного решения по отношению к невозмущенному при t → +∞, в частности, существует ли для любого ε > 0 такое δ > 0, что

и исследуем зависимость поведения возмущенного решения от параметра λ, т. е. проведем классификацию уравнения (1.18.1) по устойчивости.

1. λ = 0 = x ≡ x0, поэтому при |x0| < δ |x| = |x0| < ε, причем в

невозмущенное решение также устойчиво в смысле Ляпунова. К тому же невозмущенное решение “притягивает” все возмущенные:

lim x0eλ(t−t0) = 0.

t→+∞

В этом случае говорят, что невозмущенное решение асимптотически устойчиво в смысле Ляпунова.

3. λ > 0. Здесь каким бы малым мы не взяли x0, мы не обеспечим заданную малость (1.18.2) при всех t > t0. В этом случае невозмущенное решение неустойчиво в смысле Ляпунова.

Теперь расмотрим уравнение

причем будем считать, что правая часть удовлетворяет условиям теоремы существования и единственности (теоремы Пикара) в некоторой области D, и выполняется равенство f (t, 0) = 0 при всех значениях t > t0. Тогда x ≡ 0 – единственное решение, удовлетворяющее начальному условию x0(t0) = 0. Это решение мы будем считать невозмущенным. Возмущенными решениями являются все решения, соответствующие значениям x0 6= 0. Мы предполагаем, что они определены для всех t > t0.

Невозмущенное решение называется устойчивым в смысле Ляпунова (при t → +∞), если

ε > 0 δ > 0 : |x0| < δ = |x(t; t0, x0)| < ε t > t0.

62

В противном случае невозмущенное решение называется неустойчивым в смысле Ляпунова. Если для устойчивого невозмущенного решения имеет место “притяжение”

lim x(t; t0, x0) = 0

t→+∞

в некоторой окрестности x0, то невозмущенное решение называется асимптотически устойчивым. Очевидно, устойчивость в смысле Ляпунова представляет собой непрерывную зависимость от начального значения x0 равномерно относительно t на всем полубесконечном интервале [0, +∞) (а не на конечном интервале, как указывается в теореме 2, см. Введение).

Применим приведенные определения к особым точкам, рассмотренным в классификации предыдущего раздела. Как уже указывалось, нулевое решение системы (1.17.5) x ≡ 0, y ≡ 0 является состоянием покоя, и его траектория состоит из одной точки x = 0, y = 0 (точки покоя). Решение x = x(t), y = y(t) можно рассматривать как движение точки, аргумент t в данном случае имеет смысл времени. При рассмотрении различных особых точек мы будем придерживаться обозначений переменных, использованных в предыдущем разделе. Переходя к равносильному системе (1.17.5) уравнению (1.17.6), рассмотрим сначала уравнение

dudv = −uv .

Оно имеет нулевое решение, а всякое возмущенное решение с начальными условиями (u0, v0) можно записать в параметрической форме

u= u0 cos t + v0 sin t,

v= −u0 sin t + v0 cos t.

Очевидно, что

|u| = |u0 cos t + v0 sin t| 6 |u0| + |v0|,

|v| = |−u0 sin t + v0 cos t| 6 |u0| + |v0|,

т. е. для любого ε > 0 найдется соответствующее δ > 0, и невозмущенное движение устойчиво по Ляпунову. Траектория невозмущенного движения

– точка покоя (0, 0), траекториями возмущенного являются окружности u2 + v2 = u20 + v02. Легко видеть, что асимптотической устойчивости нет (рис. 7).

63

Рис. 7.

Рассмотрим теперь уравнение

dηdξ = 2ξη .

Здесь нулевое решение неустойчиво, так как семейство возмущенных

решений имеет вид

ξ = ξ et,

η= η0e2t, (1.18.4)

икакие бы малые ненулевые отклонения мы ни брали, при t → +∞ тра-

ектория уходит сколь угодно далеко от точки покоя. Такой узел неустойчив. Однако другой выбор параметризации0

ξ = ξ0e−t, (1.18.5)

η = η0e−2t,

превращает этот узел в устойчивый, причем асимптотически устойчивый в целом (это означает, что начальные значения ξ0 и η0 можно брать сколько угодно большими, т. е. область притяжения занимает всю плоскость). Таким образом, узел может быть как устойчивым, так и неустойчивым в зависимости от того, какова была исходная система первого приближения (1.17.5) – случаю (1.18.4) соответствует система

dξ = ξ,

dt

dη

dt = 2η,

(корни уравнения (1.17.8) положительные), случаю (1.18.5) – система

dξ = −ξ,

dt

dη

dt = −2η

64

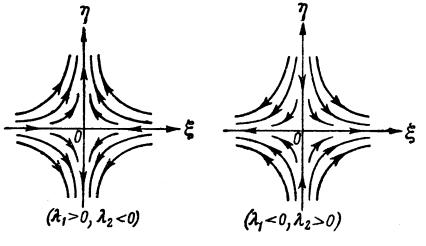
(корни уравнения (1.17.8) отрицательные), однако равносильные им уравнения совпадают. Напомним, что в определении устойчивости мы заведомо фиксируем “направление времени” – t [t0, +∞). Изменение направления времени, естественно, меняет и поведение возмущенных решений (меняется направление стрелок на фазовых портретах). На рис. 8 показаны устойчивый и неустойчивый узлы.

Рис. 8.

Теперь легко находим, что в случае фокуса невозмущенное движение будет асимптотически устойчиво, если корни уравнения (1.17.8) имеют отрицательную вещественную часть, и неустойчиво в противном случае (на рис. 9 показан устойчивый фокус).

Рис. 9.

Наконец, уравнение

dηdξ = −ηξ

65

имеет неустойчивое нулевое решение – общее решение в форме Коши мож-

но записать в виде

ξ = ξ e−t,

η= η0et, (1.18.6)

т.е. особая точка типа “седло” всегда неустойчива. Однако, если ограничиться возмущенными решениями, подчиняющимися дополнительному

условию η0 = 0, то такие решения оказываются устойчивыми. Поэтому нулевое решение здесь называют условно устойчивым. На рис. 10 пока-

заны условно устойчивые особые точки типа “седло” – с дополнительным условием η = 0 и ξ = 0 соответственно0

Рис. 10.

1.19.Задача программного управления

где u = u(t) – управление. Мы будем считать, что функция u(t) выбирается из некоторого множества U допустимых управлений, а уравнение (1.19.1) имеет единственное решение при любом u U .

Задача программного управления состоит в разыскании допустимого управления u(t), при котором уравнение имеет решение x(t), удовлетворяющее условиям x(0) = x0, x(T ) = xT . Если такое управление существует, его называют программным, а пару точек (x0, xT ) – управляемой на [0, T ]. Если каждая пара точек x1, x2 на [0, T ] управляема, уравнение (1.19.1) называется полностью управляемым.

Легко видеть, что задача программного управления является одной из разновидностей краевых задач – решение уравнения (1.19.1) должно удовлетворять некоторым условиям в двух точках. Вместе с тем, для

66

уравнения (или системы) первого порядка “двухточечная” задача переопределена – корректной задача будет лишь в случае задания условия в одной точке. Добавление “лишнего произвола” может, напротив, привести к недоопределенности, поэтому часто выбирают управление из определенного класса (например, исходя из простоты практической реализации). Одним из часто применяемых классов управлений является релейное управление, построенное на основе кусочно-постоянных функций. В простейшем случае

(режим “включено – выключено”).

Рассмотрим простейшую задачу: пусть уравнение имеет вид

причем x0 = xT = 0. Покажем, что u не может быть константой, но программное управление найдется в классе релейных. Общее решение уравнения (1.19.2) запишется в виде

Z

x = eat C + u(t)e−atdt .

Если u = u0 = const, получим

x = Ceat − ua0 ,

откуда, исходя из первого краевого условия, C = u0/a. Тогда

x(τ ) = ua1 (eaτ − 1). На втором интервале мы, по существу, решаем другое дифференциальное уравнение

dx

dt = ax + u2

67

с краевыми условиями x(τ ) = ua1 (eaτ − 1), x(T ) = 0. Первое условие

здесь является условием “стыковки” – так как мы ищем непрерывное решение, естественно требовать, чтобы

Поэтому (с учетом первого условия) решение второго уравнения имеет

вид

x(t) = a1 u1 + e−aτ (u2 − u1) eat − ua2 .

Второе краевое условие нашей задачи выполняется, если положить

u1 (eaτ − 1) + u2 1 − ea(τ −T ) = 0.

Таким образом, релейное управление позволяет решить задачу, причем требуется всего одно переключение. Это может быть существенно, если используется “одноразовый” переключатель, например, пиропатрон в ракете.

Тем не менее заметим, что в данном примере x˙ в точке t = τ терпит

что вполне естественно, если учесть, что по существу решается уравнение с разрывной правой частью. Заметим также, что у исследователя остается еще выбор величины одного из управлений, а также “точки переключения”

τ .

68

Глава 2. Уравнения старших порядков

До последнего времени основным методом решения уравнений старших порядков являлось понижение порядка. Основная цель метода – свести исходное уравнение к интегрированию уравнения первого порядка. Альтернативой этому подходу служит поиск преобразований, приводящих исходное уравнение к линейному, т. е. поиск преобразований линеаризации. При этом порядок уравнения может даже повышаться – так, уравнение Риккати (первого порядка) легко сводится к линейному однородному уравнению второго порядка. Лишь в 80-е годы XX века с развитием дискретно-группового анализа [5] получили распространение методы, существенно использующие повышение порядка (метод RF -пар и родственные ему). Более того, широкие классы уравнений первого порядка (в частности, уравнений Абеля второго рода) были проинтегрированы именно этими методами.

2.1.Простейшие случаи понижения порядка

1.Автономные уравнения. Автономными уравнениями называются уравнения, не содержащие явно аргумента искомой функции x. Это означает, что любое такое уравнение инвариантно относительно любого переноса вдоль оси x. Инвариантом этого преобразования будет переменная y, а также производные y любого порядка. Поэтому порядок урав-

понижается на единицу преобразованием y′(x) = p(y), т. е. функция y становится новой независимой переменной, а искомой функцией становится производная y′(x). Вторая производная, очевидно, вычисляется по формуле

третья – по формуле y′′′ = p2p′′ + p(p′)2, и так далее. В результате получается уравнение порядка (n − 1)

Заметим, что в случае, когда порядок уравнения можно понизить несколькими различными способами, данным способом следует поьзоваться в последнюю очередь, так как при таком понижении порядка резко повышается нелинейность уравнения. Если известно решение уравнения (2.1.2) –

69

функция p(y), то решение уравнения (2.1.1) записывается в параметрической форме:

инвариантны относительно любого переноса вдоль оси y. Инвариантом этого преобразования будет переменная x, а также производные y любого порядка. Поэтому порядок уравнения (2.1.3) понижается на единицу преобразованием y′(x) = u(x), производные всех порядков выражаются стереотипно: y(k) = u(k−1), и в результате получается уравнение

В отличие от предыдущего случая данное преобразование не “портит” вида уравнения. В частности, линейное уравнение переводится снова в линейное. Если известно решение уравнения (2.1.4) – функция u(x), то решение уравнения (2.1.3) записывается в явном виде:

Z

y(x) = u(x) dx + C.

Если в исходном уравнении не содержатся явно ни функция y, ни ее производные до порядка s включительно, преобразование y(s+1) = u(x) понижает порядок этого уравнения на s единиц.

3. Однородные уравнения. В отличие от уравнений первого порядка, уравнения старших порядков называются однородными, если они однородны по переменной y, т. е. инвариантны по отношению к растяжению по переменной y. Простейшим критерием является тест-подстановка y → αy – уравнение однородно, если все коэффициенты α сократятся. Очевидно, уравнение

будет однородным, если функция F является однородной функций измерения 1 переменной y и всех ее производных, т. е. удовлетворяет условию

70