de1

1.15.Уравнения, не разрешенные относительно производной

Рассмотрим теперь уравнения, не разрешенные относительно первой производной, т. е. уравнения общего вида (0.1.2). Предположим, что оно допускает параметрическое представление

так что

F ϕ(u, v), ψ(u, v), χ(u, v) = 0

при всех значениях параметров u, v. Используя представление (1.15.1) и соотношение dy = y′dx, всегда можно привести уравнение (0.1.2) к уравнению, разрешенному относительно производной. Очевидно,

Подставляя эти выражения в соотношение dy = y′dx, получаем

Если взять, например, u за независимую переменную, получим уравнение вида (0.1.1)

dv

du

= f (u, v),

и если найти его общее решение v = ω(u, C), то общее решение уравнения (0.1.2) запишется в параметрической форме

x = ϕ u, ω(u, C) , y = ψ u, ω(u, C) .

Этот метод носит название метода введения параметра, в Справочнике Э. Камке он назван “интегрированием посредством дифференцирования”. Основная сложность практического применения этого метода состоит в отсутствии алгоритма подбора параметрического представления (1.15.1). В общем случае представление приходится просто угадывать. Однако выбор параметра весьма прост, если уравнение разрешимо относительно искомой функции или аргумента.

Пример 3. Пусть уравнение (0.1.2) разрешимо относительно искомой функции, т. е. может быть записано в виде

В этом случае за параметры можно принять x и y′. Представление (1.15.1) будет иметь вид

x = x, y = ϕ(x, y′), y′ = y′.

51

Обозначая переменную y′ буквой p, получим представление уравнения (1.15.2) в виде

y = ϕ(x, p), y′ = p.

Вычисляя дифференциал и подставляя dy = p dx, получаем дифференциальное уравнение

Общее решение p = ω(x, C) уравнения (1.15.4) дает общее решение уравнения (1.15.2)

в явном виде

y = ϕ x, ω(x, C) .

Уравнение (1.15.3) может иметь особое решение p = γ(x). Оно дает решение y =

В этом случае за параметры можно принять y и y′. Представление (1.15.1) будет иметь вид

y = ϕ(x, p), y′ = p.

Вычисляя дифференциал и подставляя dy = p dx, получаем дифференциальное урав-

Если найден общий интеграл p = ω(y, C) уравнения (1.15.7), общий интеграл уравнения (1.15.5) может быть получен в виде обратной функции

52

Аналогично примерам предыдущего раздела в качестве параметра возьмем y′ = p,

и, вычисляя дифференциал, получаем

Нетрудно видеть, что это уравнение – линейное относительно функции x(p):

(корни уравнения ϕ(p) − p = 0 будут исследоваться отдельно). Как известно (см. раздел 1.2), общее решение уравнения (1.16.4) имеет вид x = A(p)C + B(p). Подставляя это выражение в представление (1.16.2), получим y = A(p)ϕ(p)C +B(p)ϕ(p)+ψ(p). Таким образом, общее решение уравнения Лагранжа (1.16.1) в параметрической форме будет

x= A(p)C + B(p),

y= A(p)ϕ(p)C + B(p)ϕ(p) + ψ(p).

Исследуем теперь случаи, когда знаменатель в уравнении (1.16.4) обращается в нуль. Очевидно, корни уравнения

дают нам решения уравнения (1.16.3) в виде

y = pix + ψ(pi), i = 1, 2, . . . ,

где pi – корни уравнения (1.16.5). Эти решения могут быть как частными, так и особыми. Таким образом, особыми решениями уравнения Лагранжа могут быть только прямые.

Уравнение Лагранжа можно проинтегрировать и другим способом. Преобразование Лежандра (0.2.2) переводит уравнение (1.16.1) сразу в линейное уравнение 1-го порядка

Нетрудно проверить, что окончательное решение совпадает с полученным выше. Покажем это. Запишем точное решение уравнения (1.16.4) согласно (1.2.4):

53

Простыми преобразованиями можно привести это выражение к форме, не содержащей производных функций ϕ и ψ:

Аналогично, решение уравнения (1.16.6) запишется в виде

(1.16.8) Если учесть, что x = y¯′, то очевидно, что выражение для x мы получим, продифференцировав (1.16.8) по x¯. При этом после замены x¯ = p получается формула, идентичная (1.16.7).

Если в уравнении Лагранжа ϕ(y′) ≡ y′, свойства уравнения диаметрально меняются. Уравнение

называется уравнением Клеро. Уравнение (1.16.3) приобретает вид

[x + ψ′(p)] dp = 0,

распадаясь на два:

Первое из этих уравнений дает нам общее решение уравнения Клеро – из p = C следует

Таким образом, общее решение представляет собой семейство прямых (сравните – у уравнения Лагранжа прямыми могли быть только особые решения). Второе уравнение (1.16.10) – алгебраическое, оно дает выраже-

ние x через параметр p

x = −ψ′(p).

Если подставить это выражение в исходное уравнение (1.16.9), заменив y′ на p, получим еще одно решение уравнения Клеро в параметрической

54

Если применить к уравнению Клеро преобразование Лежандра (0.2.2), то мы сразу получаем алгебраическое уравнение y¯ = −ψ(¯x), которое, как нетрудно проверить (см. уравнение Лагранжа), дает нам особое решение (1.16.12). Общее решение уравнения Клеро применением касательных преобразований получить невозможно – вторая производная y′′, согласно (1.16.11), равна нулю, и при обращении преобразования Лежандра возникает неопределенность. Однако этот факт не следует считать ограничением для применения касательных преобразований – наличие решений вида y = Ax + B нетрудно проверить прямой подстановкой.

1.17.Особые точки

Мы будем рассматривать уравнение (0.1.1) и наряду с ним перевернутое уравнение

которое будет использоваться в окрестности тех точек, в которых f (x, y) обращается в бесконечность. Точка (x0, y0) называется особой точкой уравнения (0.1.1), если в любой достаточно малой окрестности ее правые части уравнений (0.1.1) и (1.17.1) не удовлетворяют условиям теоремы Пикара. Особая точка называется изолированной, если в некоторой достаточно малой окрестности ее нет других особых точек. В качественной теории дифференциальных уравнений показывается, что знание конфигурации особых точек (т. е. их расположения на плоскости (x, y)) и поведения интегральных кривых в их окрестностях позволяет, в принципе, судить о поведении интегральных кривых во всей области задания ОДУ.

Прежде, чем мы будем изучать особые точки уравнения (0.1.1), укажем, что эта задача эквивалентна изучению точек покоя (равновесия) автономной системы второго порядка

dt

где t – время, а x и y – координаты точки на фазовой плоскости (x, y). Если в точке (x0, y0) функции P (x, y) и Q(x, y) обращаются в нуль, система (1.17.2) имеет решение x ≡ x0, y ≡ y0 – состояние покоя. Такая точка и называется точкой равновесия (покоя) системы (1.17.2).

Система (1.17.2) равносильна уравнению

55

в том смысле, что каждая интегральная кривая уравнения (1.17.3) является траекторией системы (1.17.2) на фазовой плоскости и обратно, каждая траектория системы (1.17.2) на фазовой плоскости, отличная от точки равновесия x = x0, y = y0 есть интегральная кривая уравнения (1.17.3). Поэтому точка равновесия системы (1.17.2) является, вообще говоря, особой точкой соответствующего ей уравнения (1.17.3).

Во многих приложениях функции P (x, y) и Q(x, y) являются голоморфными функциями своих аргументов, и их часто представляют в виде

P (x, y) = ax + by + εϕ(x, y),

(1.17.4)

Q(x, y) = cx + dy + εψ(x, y),

где ϕ(x, y) и ψ(x, y) – полиномы (или ряды) по переменным x, y, содержащие слагаемые с суммарной степенью переменных, б´ольшей единицы. Если ε достаточно мало, то, удерживая в системе (1.17.2) с правой частью (1.17.4) только слагаемые первого порядка, получаем систему первого при-

dt

А. Пуанкаре (Henri Poincar´e) доказал, что если особые точки нелинейной системы (1.17.2) имеют тип, гомеоморфный типу особой точки линейной системы (1.17.5), то “фазовый портрет” системы (1.17.2) в окрестности особой точки совпадает с таковым у линейной системы (1.17.5).

Классификацию особых точек по первому приближению также связывают с именем Пуанкаре. Рассмотрим уравнение (1.17.3), равносильное

в предположении, что ad − bc =6 0, и выполним линейное преобразование

ξ = αx + βy, η = γx + δy.

Преобразованное уравнение будет иметь вид

Потребуем, чтобы в числителе был моном λη, а в знаменателе – моном µξ. Приравнивая в числителе и знаменателе коэффициенты при x и y, получим для определения неизвестных коэффициентов α, β, γ, δ две

56

Нетривиальные решения этих систем существуют, если

т. е. λ и µ являются корнями одного и того же уравнения

Пусть корни различны (λ1 =6 λ2). Тогда из систем (1.17.7) находим α, β, γ, δ, причем оказыватся, что

α β

=6 0.

γ δ

Уравнение (1.17.6) приобретает вид

dη = λ1η , dξ λ2ξ

его общее решение

λ1

η = C|ξ|λ2 .

1. Корни λ1 и λ2 – действительные и одного знака. Без ограничения общности можно считать, что λ1 > λ2 > 0. Все интегральные кривые проходят через начало координат ξ = η = 0 и касаются в этой точке оси

Прямая ξ = 0 тоже является решением. Такая особая точка называется узлом. Узел такого типа показан на рис. 1. Через узел проходит бесконечное множество интегральных кривых.

2. Корни λ1 и λ2 – действительные и разных знаков. Тогда

η = C|ξ|−k, k > 0.

Двумя решениями в данном случае являются прямые ξ = 0 и η = 0, остальные интегральные кривые не проходят через особую точку. Такая особая точка называется седлом (рис. 2)

57

3. Корни λ1 и λ2 – комплексно-сопряженные:

λ1 = p + qi, λ2 = p − qi.

При определении γ и δ, а также α и β , можно подобрать постоянный множитель (так как уравнения в каждой паре пропорциональны) так, чтобы

или

du(pv − qu) = dv(pu + qv).

Это можно переписать в виде

и, после деления на u2 + v2 проинтегрировать, получив общее решение

2В этом и следующем разделах рисунки заимствованы из книги [19].

58

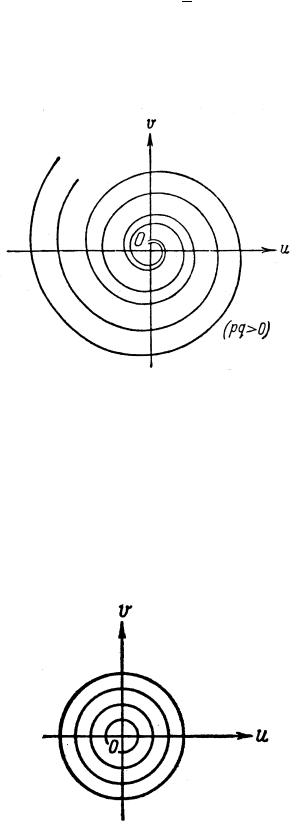
Это выражение принимает более привычный вид, если перейти к полярным координатам на плоскости u = r cos ϕ, v = r sin ϕ:

r= C exp −pq ϕ ,

т. е. мы имеем семейство логарифмических спиралей с асимптотической точкой в центре. Все кривые примыкают к началу, но без определенной предельной касательной, так как делают бесконечное число оборотов (рис. 3)

Рис. 3.

Эта особая точка – фокус.

4. Корни λ1 и λ2 – чисто мнимые (сопряженные): λ1 = qi, λ2 = = −qi. Повторяя выкладки п. 3, получим уравнение (1.17.9), но при p = 0, т. е.

udu + vdv = 0,

общее решение которого будет u2 + v2 = C. Это семейство замкнутых кривых (в координатах u, v – окружностей). Через саму особую точку не проходит ни одна интегральная кривая (рис. 4)

Рис. 4.

59

уравнений независмым является только одно, так как определитель системы (1.17.10) совпадает с дискриминантом уравнения (1.17.8) и в силу равенства корней обращается в нуль. Возьмем любое решение ξ =

взять η = y. В результате перехода к новым переменным (x, y) → (ξ, η) получаем однородное (и одновременно линейное) уравнение

dηdξ = ηξ + λ1 .

Его общее решение

η = λ1 ξ ln ξ + Cξ.

Интегральной кривой является также ξ = 0. Все кривые проходят через начало, причем угловой коэффициент их касательных равен ±∞ (знак зависит от знака λ). Эта особая точка – узел (рис. 5), существенно отличающийся от узла п. 1 (в котором одна из интегральных кривых имела отличный от других угловой коэффициент)

Рис. 5.

60