de1

в точности равна n, и уравнение имеет n корней. Поэтому общее решение уравнения Эйлера записывается в виде

n

X

Для подробного изучения форм и свойств решения (2.10.3) можно воспользоваться подстановкой (2.1.9), которая приводит более общее уравнение (2.1.8), тоже инвариантное относительно растяжений по x, к автономному виду. При этом уравнение (2.10.1) приводится к линейному уравнению с постоянными коэффициентами. Рассмотрим в качестве примера линейное уравнение Эйлера 2-го порядка

Таким образом, решением исходного уравнения (2.10.4) будет (после подстановки t = ln x)

Совершенно аналогично решается и неоднородное уравнение Эйлера.

2.11.Задача Штурма–Лиувилля

Задачей Штурма–Лиувилля или краевой задачей на собственные значения называется задача поиска нетривиальных (не равных нулю тождественно) решений линейного однородного уравнения с переменными коэффициентами

101

на промежутке (a, b), удовлетворяющих однородным краевым условиям

y(a) = 0, y(b) = 0 (2.11.2)

(точки a и b могут быть и бесконечно удаленными). Функции p(x), q(x) и r(x) – непрерывные и неотрицательные на рассматриваемом промежутке.

Задачи на собственные значения возникают в математической физике при применении метода разделения переменных (метода Фурье). Как правило, в качестве условий задаются значения искомой функции в некоторый начальный момент времени (t = t0) и на границах исследуемой области. Поэтому по временн´ой координате ставится задача Коши, а по пространственным – краевая. При этом функции p(x) и r(x) в той или иной степени отражают “геометрию” задачи (они возникают, в частности, как коэффициенты Ламе при переходе от декартовой к криволинейным координатам), а функция q(x) является потенциальной.

Вообще говоря, ниоткуда не следует, что задача (2.11.1)–(2.11.2) имеет нетривиальное решение. В ряде случаев оно существует лишь при определенных значениях параметра λ. Множество Λ таких значений называется спектром задачи. Числа λj Λ называются собственными числами задачи, а соответствующие им решения yj (x) – собственными функциями.

Свойства нетривиальных решений задачи (2.11.1)–(2.11.2) формулирует следующая теорема [21].

Теорема 4. При p(x) > 0 на [a, b]

1. Существует счетное множество собственных чисел λ1 < λ2 <

. . . < λn . . . , которым соответствуют нетривиальные решения задачи – собственные функции y1(x), y2(x), . . . , yn(x), . . . .

2.При q(x) > 0 все собственные числа λj положительны.

3.Собственные функции ym(x), yn(x) при m 6= n ортогональны

между собой с весом r(x) на отрезке [a, b]

Zb

r(x)ym(x)yn(x) dx = 0 (m =6 n).

a

4. (Теорема разложимости В. А. Стеклова). Произвольная функция F (x), дважды непрерывно дифференцируемая и удовлетворяющая граничным условиям F (a) = F (b) = 0, разлагается в равномерно и абсолютно сходящийся ряд по собственным функциям yj (x):

102

где kynk – норма yn

Zb

kynk2 = yn2 (x)r(x) dx.

a

Заметим, что если функция p(x) обращается в нуль на концах промежутка, теорема 4 формулируется несколько иначе [21] (здесь мы эту формулировку не приводим). Докажем свойство 3, но сначала выведем одну полезную формулу. Пусть u(x) и v(x) – произвольные функции, дважды дифференцируемые на интервале (a, b) и имеющие непрерывную первую производную на отрезке [a, b]. Введем дифференциальный оператор

и рассмотрим выражение

uL[v] − vL[u] = u(pv′)′ − v(pu′)′ = [p(uv′ − u′v)]′.

Интегрируя это равенство по x от a до b, получим формулу Грина

Zb

(uL[v] − vL[u]) dx = p(uv′ − u′v)|ba .

a

Теперь пусть ym(x), yn(x) – две собственные функции, соответствующие собственным числам λm, λn. Полагая в формуле Грина u = ym(x), v = yn(x) и учитывая граничные условия, находим

Zb

(ymL[yn] − ynL[ym]) dx = 0,

a

откуда, воспользовавшись исходным уравнением (2.11.1), получаем

Zb

(λn − λm) yn(x)ym(x)r(x) dx = 0.

a

Таким образом, если λm =6 λn, то имеет место условие

Zb

yn(x)ym(x)r(x) dx = 0,

a

выражающее ортогональность с весом r(x) собственных функций ym(x) и yn(x).

103

Пример 7. Рассмотрим простейшую задачу Штурма–Лиувилля, возникающую при решении задачи о колебании струны. Уравнение имеет вид

краевые условия соответствуют закреплению струны с обоих концов:

(l – длина струны). Очевидно, здесь p(x) = 1, q(x) = 0, r(x) = 0, a = 0, b = l. 1. λ < 0. Тогда общее решение уравнения (2.11.3) имеет вид

√√

y(x) = C1e −λx + C2e− −λx.

Подставляя граничные условия (2.11.4), получим систему алгебраических уравнений

(

C1 + C2 = 0,

√√

C1e −λl + C2e− −λl = 0.

Определитель этой системы заведомо не равен нулю (при λ 6= 0, l =6 0), поэтому система совместна, но имеет лишь тривиальное решение C1 = C2 = 0.

2. λ = 0. Общее решение уравнения (2.11.3) имеет вид

y(x) = C1x + C2,

иотсутствие нетривиального решения краевой задачи очевидно.

3.λ > 0. В этом случае общее решение уравнения (2.11.3) имеет вид

все множество {yk } образует базис гильбертова пространства (ортогональность функций (2.11.5) весьма несложно проверить), любая функция, удовлетворяющая условиям теоремы 4 (п. 4), может быть разложена в ряд Фурье по этому базису.

2.12.Задача о “провисании” потенциала

Задача об изменении потенциала вдоль бесконечно широкого пучка электронов первоначально решалась в связи с расчетом токопрохождения в многоэлектродных лампах (см., например, [22]). Здесь мы ее приводим как простейший пример решения краевой задачи для нелинейного уравнения.

104

Сначала рассмотрим поток электронов в обычной двухэлектродной вакуумной лампе – диоде. Если катод имеет нулевой потенциал, а анод – потенциал Ua, в отсутствие свободных электронов в межэлектродном промежутке потенциал V растет линейно от катода к аноду. Однако вследствие термоэмиссии электроны с поверхности катода попадают в межэлектродный промежуток, где возникает объемный или пространственный заряд электронов с плотностью ρ. Таким образом, эмитированные катодом электроны движутся в суммарном электрическом поле, задаваемом электродами и собственным объемным зарядом электронов. Поле определяется уравнением Пуассона

где – оператор Лапласа, ε0 – диэлектрическая проницаемость (мы считаем ее константой). Пусть катод и анод являются бесконечными плоскими пластинами по осям x, y, а поток электронов направлен по нормали к этой поверхности, т. е. в направлении оси z. В данном случае мы можем рассматривать нашу задачу как одномерную, и уравнение (2.12.1)

К этому соотношению следует добавить уравнение неразрывности

∂ρ

∂t

+ div j = 0,

где j – вектор плотности тока. В силу стационарности (dρ/dt = 0) и одномерности задачи имеем dj/dz = 0, т. е. j = ρv = const вдоль оси z (v – скорость потока электронов). С учетом этого уравнение Пуассона (2.12.2) перепишется в виде

где j – z-проекция плотности электронного тока (остальные проекции равны нулю). Величину v можно найти из закона сохранения энергии

mv2 2 −eV = C, где m – масса электрона, e – заряд электрона, C – полная энергия, которая в данном случае равна нулю, так как в начальной точке (в катоде) скорость электрона и потенциал – нулевые. Полагая e/m = η

105

Граничные условия задачи в данном случае определяют задачу Ко-

Это выражение носит название закона Ленгмюра или закона “трёх вторых” и связывает плотность тока и анодное напряжение диода при заданном расстоянии между электродами.

Теперь рассмотрим поток электронов, заполняющий все пространство между двумя бесконечными параллельными плоскими электродами A и B, и движущийся в направлении нормали к электродам, которую примем за ось z (рис. 11)3:

Рис. 11.

Потенциалы электродов A и B одинаковы и равны V0, а потенциал катода равен нулю. Примем, что скорости электронов и плотность тока j во всех точках каждой плоскости, перпендикуларной оси z, имеют одинаковые значения, т. е. все физические величины будут зависеть лишь от

3Рисунки данного раздела заимствованы из книги [23].

106

осевой координаты z, поэтому задачу также можно рассматривать как одномерную. Искомой величиной является распределение потенциала в пространстве между электродами A и B [23].

Граничные условия задачи имеют вид

Скорость электронов в минимуме потенциала (т. е. в точке z = l/2) определяется выражением vMIN = √2ηVMIN. Поэтому нетрудно видеть, что правая часть уравнения (2.12.5) пропорциональна разности скоростей электронов в произвольной точке z и в точке z = l/2. С ростом плотности тока j потенциал в минимуме уменьшается и при большой плотности может достигать нуля. В этом случае (VMIN = 0) электроны, дойдя до среднего сечения, останавливаются, в пучке возникает неподвижное электронное облако (“виртуальный катод”), и нормальное прохождение тока нарушается.

Повторное интегрирование (уравнение (2.12.5) – тоже автономное!) после несложных преобразований дает

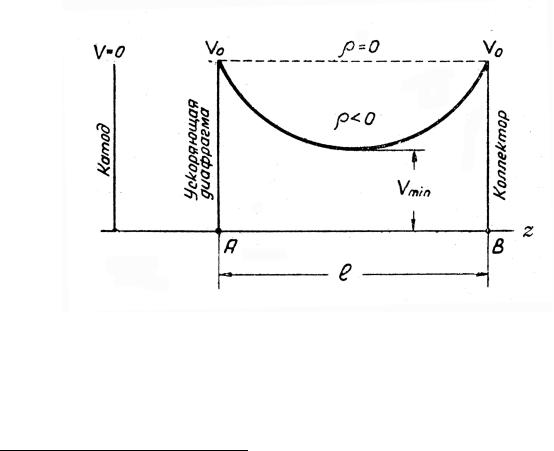
Полагая z = 0, из (2.12.6) получаем зависимость отношения потенциала

потенциала в минимуме не соответствует “обратному ходу” вдоль кривой,

107

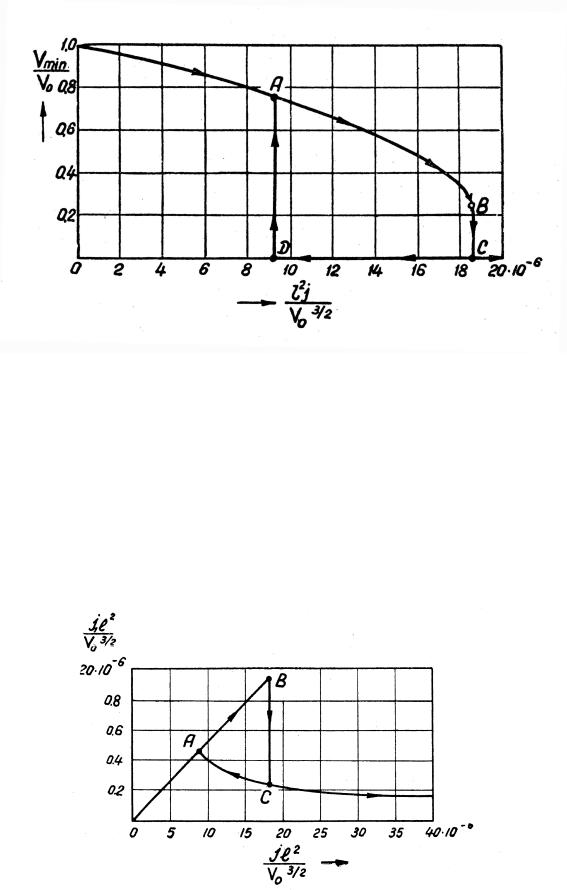
Рис. 12.

При тех плотностях тока пучка на входе в систему, для которых потенциал в средней точке падает до нуля, пучок электронов распадается как бы на два диода: от первого электрода (диафрагма) до виртуального катода и от виртуального катода до второго электрода (коллектора). К каждому из этих диодов можно применить закон трех вторых, и если обозначить плотность тока через коллектор через j1, можно построить

гистерезисный характер) показан на рис. 13.

Рис. 13.

108

В заключение заметим, что рассмотренная в данном разделе краевая

задача имеет на некотором подмножестве области изменения параметра

l2j

3/2 три решения, как это следует из формулы (2.12.6), причем два

V0

из них – условно устойчивы (одно – при условии роста параметра, второе

– при условии его уменьшения), а третье – неустойчивое (на рис. 12 оно не показано).

109

Глава 3. Элементы аналитической теории дифференциальных уравнений

3.1.Обобщенный степенной ряд. Особые точки уравнения

где p(x) и q(x) являются голоморфными в окрестности некоторой точки

сходятся при |x − x0| < r. Тогда, согласно теореме Коши, существует единственное решение, голоморфное в той же окрестности и принимающее

k=2

В приложениях часто встречаются случаи, когда коэффициенты уравнения – полиномы или отношения полиномов. В первом случае ряд (3.1.2) сходится при всех x, во втором – радиус сходимости не меньше, чем расстояние от x = x0 до ближайшего нуля знаменателей функций из (3.1.1).

Пусть x = x0 – особая точка уравнения (3.1.1). Тогда в общем случае решение не будет голоморфным ни в какой окрестности этой точки. Например, уравнение Бесселя

имеет особую точку x = 0. Несложные преобразования (z = √xy) позволяют найти фундаментальную систему решений

Решения не голоморфны в окрестности x = 0, но представимы в виде рядов

110