
- •Глава I. Теоретические и методические аспекты изучения линий второго порядка
- •1.1. Теория линий второго порядка и использования икт в обучении
- •1.2. Методические аспекты изучения линий второго порядка в школьном курсе алгебры 7-9 классов
- •Глава II. Практическое применение икт при изучении линий второго порядка учащимися
- •Глава I. Теоретические и методические аспекты изучения линий второго порядка
- •1.1. Теория линий второго порядка и использования икт в обучении
- •Понятие линии второго порядка в аналитической геометрии
- •Приведение общего уравнения линии второго порядка к каноническому виду
- •Исследование свойств окружности по её уравнению
- •2) Симметрия окружности:
- •Исследование свойств эллипса по его уравнению
- •1) Пересечение эллипса с осями координат:
- •2) Симметрия эллипса относительно координатных осей ox и oy:
- •4) Эксцентриситет эллипса:
- •2) Симметрии гиперболы относительно координатных осей и:
- •3) Асимптоты гиперболы:
- •4) Фокусы гиперболы:
- •Линии второго порядка в элементарной математике
- •1.2. Методические аспекты изучения линий второго порядка в школьном курсе алгебры 7-9 классов
- •1.2.1. Анализ содержания темы «Линии 2го порядка» в школьных учебниках. (учебники по алгебре под редакцией г. В. Дорофеева, ш. Ф. Алимова, а. Г. Мордковича)
- •1.2.2. Особенности изучения линий второго порядка в школьном курсе алгебры
- •Глава II. Практическое применение икт при изучении линий второго порядка учащимися
- •2.1. Систематизация цор, содержащих линии второго порядка
- •2.2. Особенности использования цор в изучении линий второго порядка на уроках алгебры
- •Плюсы и минусы при использовании икт на уроках
- •Вывод уравнения окружности
- •Изображение окружности
- •Вывод уравнения эллипса
- •Изображение эллипса
- •Изображение гиперболы
- •Вывод уравнения параболы
- •Изображение параболы
4) Эксцентриситет эллипса:
Определение
2.2.
Эксцентриситетом эллипса
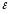 называют отношение межфокусного
расстояния 2с
к длине большой оси 2а.
называют отношение межфокусного
расстояния 2с
к длине большой оси 2а.
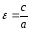 .
.
Так
как
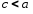 ,
следовательно,
,
следовательно,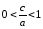 .
.
Если
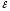 стремится к нулю при постоянном значении
стремится к нулю при постоянном значении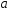 ,
то
,
то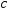 стремится к нулю. При этом величина
стремится к нулю. При этом величина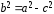 стремится к
стремится к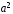 .
В предельном случаи уравнение эллипса
принимает вид:
.
В предельном случаи уравнение эллипса
принимает вид: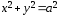 .
Это уравнение окружности. Если
.
Это уравнение окружности. Если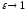 ,
то
,
то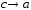 .
При этом малая ось эллипса неограниченно
уменьшается, эллипс стремится к отрезку.
(чертеж
11.)
[1.С.106]
.
При этом малая ось эллипса неограниченно
уменьшается, эллипс стремится к отрезку.
(чертеж
11.)
[1.С.106]
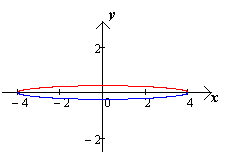
Чертеж 11.
5) Диаметры эллипса:
Всякая
хорда, проходящая через центр эллипса,
называется диаметром
эллипса.
В частности, диаметрами эллипса является
его большая ось
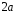 и
малая ось
и
малая ось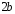 .
Всякий диаметр эллипса, не являющийся
его осью, больше малой оси, но меньше
большой оси (чертеж
12.).
[1.С.106-107]
.
Всякий диаметр эллипса, не являющийся
его осью, больше малой оси, но меньше
большой оси (чертеж
12.).
[1.С.106-107]
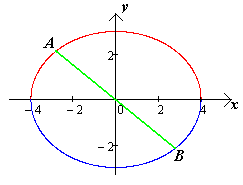
Чертеж 12.
6) Касательная к эллипсу:
Уравнение
касательной к эллипсу
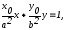 где
где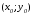 -
координаты точки касания и
-
координаты точки касания и соответственно большая и меньшая полуоси
эллипса (чертеж
13.).
соответственно большая и меньшая полуоси
эллипса (чертеж
13.).
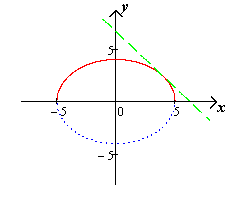
Чертеж 13.
7) Частный случай эллипса - окружность:
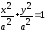
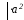
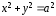 ,
где
,
где
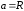 окружности.
окружности.
8) Взаимное расположение точек и эллипса:
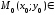 эллипсу,
если
эллипсу,
если
 верное
равенство,
верное
равенство,
Если
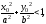 то
то лежит
внутри эллипса,
лежит
внутри эллипса,
Если
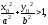 то
то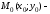 лежит
вне эллипса. [1.С.100]
лежит
вне эллипса. [1.С.100]
9) Уравнения директрис эллипса:
Пусть
эллипс задан уравнением
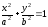 и если при этом
и если при этом
 ,
то
,
то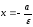 и
и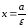 уравнения
директрис эллипса, если
уравнения
директрис эллипса, если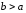 ,
то директрисы определяются уравнениями
,
то директрисы определяются уравнениями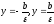 .
.
ГИПЕРБОЛА
Определение
3.1.
Гипербола -
множество точек плоскости, модуль
разности расстояний от
которых
до двух данных точек
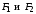 этой плоскости, называемых фокусами
гиперболы, есть заданная постоянная
величина
этой плоскости, называемых фокусами
гиперболы, есть заданная постоянная
величина меньшая,
чем расстояние между фокусами
меньшая,
чем расстояние между фокусами
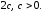 [8.С.510]
[8.С.510]
Общий
вид уравнения
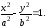
Исследование свойств гиперболы по ее уравнению
1) Пересечение гиперболы с осями координат:
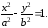
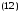
Очевидно, что гипербола состоит из двух ветвей: правой и левой, простирающихся в бесконечность.
В
уравнении (12) положим, что y=0,
получим:
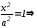
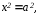 отсюда
отсюда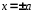 .
Следовательно, точки
.
Следовательно, точки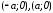 являются точками пересечения гиперболы
с осью
являются точками пересечения гиперболы
с осью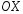 (чертеж
19.).
(чертеж
19.).
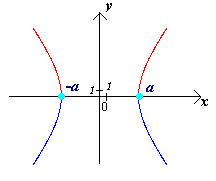
Чертеж 19.
Положим,
что в уравнении (12) х=0, и получим:
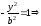
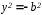 ,
следовательно, уравнение гиперболы не
пересекает ось
,
следовательно, уравнение гиперболы не
пересекает ось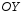 .
.
ЗАМЕЧАНИЕ:
Если мнимая ось гиперболы имеет длину
2a и направлена по оси (OX), а действительная
ось длиной 2b совпадает с осью (OY), то
уравнение гиперболы имеет вид:
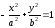 .
[1.С.107-108]
.
[1.С.107-108]
Определение
3.2.
Гиперболы, заданные уравнениями
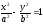 и
и
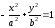 ,
называются сопряженными гиперболами.
,
называются сопряженными гиперболами.
Определение 3.3. Если a=b, гипербола называется равносторонней.
2) Симметрии гиперболы относительно координатных осей и:
Пусть
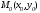 принадлежит гиперболе, то есть
принадлежит гиперболе, то есть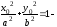 верное
равенство. Точка
верное
равенство. Точка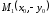 симметрична точке
симметрична точке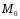 относительно
оси ОХ:
относительно
оси ОХ:
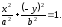
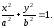 -
верное равенство. Следовательно,
-
верное равенство. Следовательно,
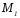 принадлежит
гиперболе, следовательно, гипербола
симметрична относительно ОХ.
принадлежит
гиперболе, следовательно, гипербола
симметрична относительно ОХ.
Точка
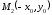 симметрична точке
симметрична точке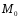 относительно оси ОУ, следовательно,
гипербола симметрична относительно
оси ОУ.
относительно оси ОУ, следовательно,
гипербола симметрична относительно
оси ОУ.
Точка
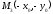 симметрична
точке
симметрична
точке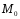 относительно О (центра), отсюда следует,
что гипербола симметрична относительно
начала координат. [1.С.108]
относительно О (центра), отсюда следует,
что гипербола симметрична относительно
начала координат. [1.С.108]
3) Асимптоты гиперболы:
Текущая точка гиперболы при движении по ней в бесконечность неограниченно приближается к некоторой прямой, которая называется асимптотой гиперболы. Асимптотами являются прямые, которые имеют следующие уравнения:
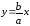 и
и
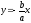 ,
,
Пусть
текущая точка гиперболы,
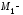 ее
проекция на ось абсцисс. Прямая
ее
проекция на ось абсцисс. Прямая
 пересекает
прямую
пересекает
прямую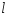 ,
заданную указанным уравнением в точке
,
заданную указанным уравнением в точке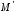 .
Докажем: что
.
Докажем: что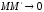 при
при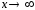 .
.
Доказательство:
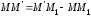 .Расстояние
.Расстояние
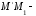 это
ордината точки
это
ордината точки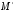 ,
лежащей на прямой
,
лежащей на прямой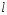 .
Она равна
.
Она равна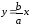 .
Расстояние
.
Расстояние это ордината точки
это ордината точки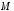 гиперболы, которую находим из её
канонического уравнения:
гиперболы, которую находим из её
канонического уравнения: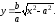 Тогда
Тогда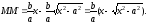
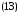
Умножим
и разделим равенство (13) на (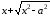 ),следовательно,
получим:
),следовательно,
получим:
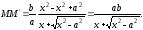
При
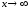 знаменатель дроби неограниченно
увеличивается, следовательно, дробь
стремится к нулю.
знаменатель дроби неограниченно
увеличивается, следовательно, дробь
стремится к нулю.
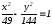 -
уравнение гиперболы, в которой
-
уравнение гиперболы, в которой
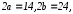 а
а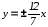 -
являются асимптотами гиперболы. (чертеж
20.)
[1.С.108]
-
являются асимптотами гиперболы. (чертеж
20.)
[1.С.108]
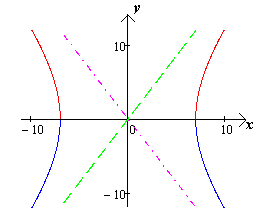
Чертеж 20.
