В силу линейности оператора Аполучаем

А(x) = x₁А(e₁)+x₂А(e₂)+…+x_nА(e_n) .

Поскольку А(е_i) (i = 1,2,...,n) — также вектор из Rⁿ, то его можно разложить по базису e₁,e₂,…,e_n . Пусть

А(e_i) = a_1ie₁+a_2ie₂+…+a_nie_n (i=1,2,…,n) (5)

Тогда

А(x) = x₁(a₁₁e₁+a₂₁e₂ +…+ a_n1e₂)+ x₂(a₁₂e₁+a₂₂e₂­+…+ a_n2e_n)+

+…+ x_n(a_1ne₁+a_2ne₂+…+ a_nne_n)= (a₁₁x₁+a₂₁x₂ +…+ a_1nx_n)e₁+

+(a₂₁x₁+a₂₂x₂ +…+ a_2nx_n)e₂+…+(a_n1x₁+a_n2x₂ +…+ a_nnx_n)e_n. (6)

С другой стороны, вектор у=А(x), имеющий в том же базисе e₁,e₂ ,…,e_n координаты у_1,у₂,…у_п можно записать так:

А(x) = y₁e₁+y₂e₂+…+y_ne_n (7)

Ввиду единственности разложения вектора по базису правые части равенств (6) и (7) равны. Поэтому

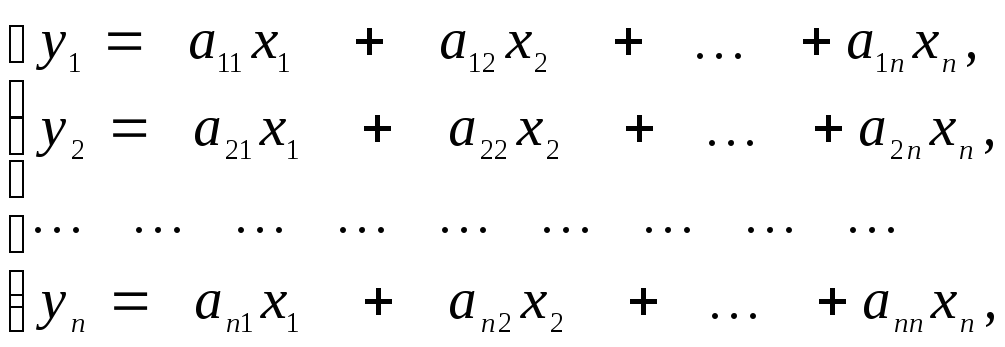
Матрица А = (а_ij) (i,j = 1,2,...,n) назьшается матрицей оператора А в базисе e₁,e₂ ,…,e_n, а ранг r матрицы А — рангом оператора А.

Таким образом, каждому линейному оператору соответствует матрица в данном базисе. Справедливо и обратное: всякой матрице п-го порядка соответствует линейный оператор п-мерного пространства.

Связь между вектором х и его образом у = А(x) можно выразить в матричной форме уравнением

У=АХ, (8)

где А — матрица линейного оператора, Х = (x₁, х₂,.…, х_n)', Y =(y₁,y₂,…,y_n)'.

Действия над линейными операторами.

Суммой двух линейных операторов А и В назьшается оператор (А+В), определяемый равенством: (А+В) (х) = А (х) + В (х).

Произведением линейного оператора А на число  называется оператор А, определяемый равенством (А(х)) = (А(х)).

Произведением линейных операторов А и В называется оператор АВ , определяемый равенством: (АВ) (х) = А(В(х)).

Можно убедиться в том, что операторы (А+В), А, АВ, полученные в результате этих действий, удовлетворяют отмеченным свойствам аддитивности и однородности, т.е. являются линейными.

Определим нулевой оператор О, переводящий все векторыпространства Rⁿ в нулевые векторы О(x)=0, и тождественный оператор Е, действующий по правилу: Е(x) = х.

Зависимость между матрицами одного и того же оператора в разных базисах выражается теоремой.

Теорема. Матрицы А и А* линейного оператора А в различных базисах e₁,e₂ ,…,e_n и e₁*,e₂* ,…,e_n* связаны соотношением

A* = C^–1AC , (9)

где С — матрица перехода от старого базиса к новому.

Собственные векторы и собственные значения линейного оператора

Вектор х0 называется собственным вектором линейного оператора А, если найдется такое число  , что

А (х) = х. (1)

Число  называется собственным значением оператора А (матрицы А), соответствующим вектору х.

Из определения следует, что собственный вектор под действием линейного оператора А переходит в вектор, коллинеарный самому себе, т.е. просто умножается на некоторое число.

Равенство (1) можно записать в матричной форме:

АХ = Х (2)

или в развернутом виде

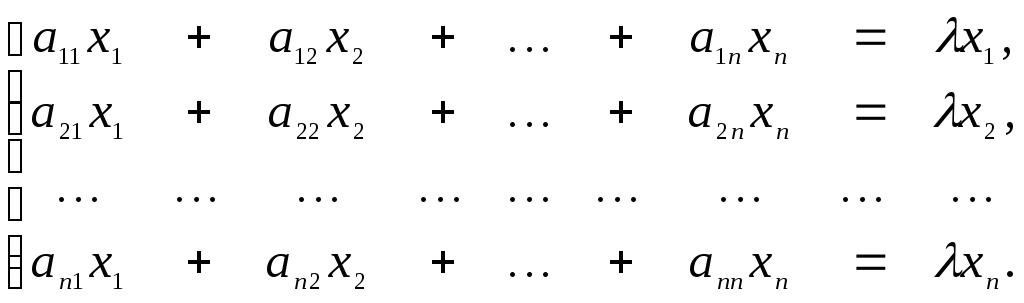
Перенесем столбец свобоных членов в левую часть системы

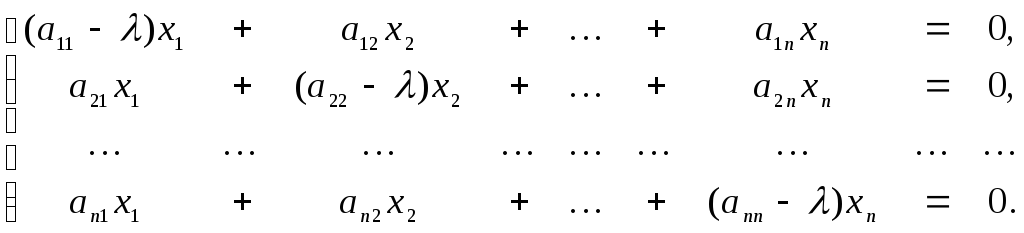
Эта однородная система всегда имеет нулевое решение х=0. Для существования ненулевого решения необходимо и достаточно, чтобы определитель системы

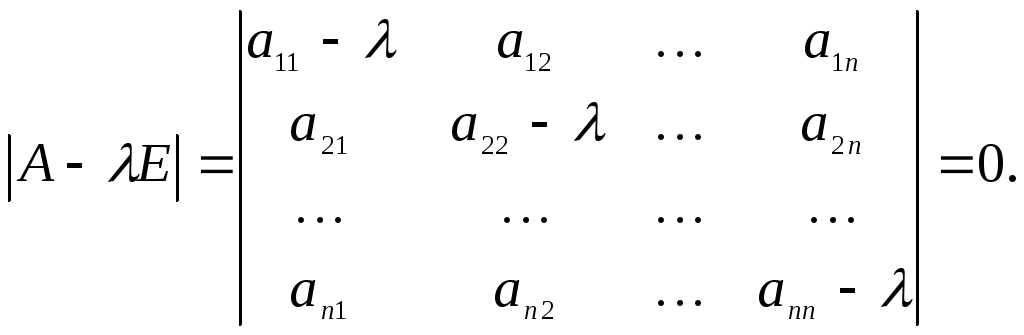(3)

Определитель является многочленомп-й степени относительно . Этот многочлен называется характеристическим многочленом оператора А или матрицы А, а уравнение (3) -—характеристическим уравнением оператора А или матрицы А.

Характеристический многочлен линейного оператора не зависит от выбора базиса. В самом деле, преобразуем характеристический многочлен , полученный в новом базисеe₁*,e₂* ,…,e_n* если известна матрица С перехода от старого базиса e₁,e₂ ,…,e_n и к новому:

Учитывая, что определитель произведения квадратных матриц равен произведению их определителей, получим

т.е.

не зависит от выбора базиса.

Наиболее простой вид принимает матрица А линейного оператора А, имеющего п линейно независимых собственных векторов e₁,e₂,…,e_n, с собственными значениями, соответственно равными ₁,₂,…,_n. Векторы e₁,e₂,…,e_n примем за базисные.

Тогда А(е_i) = _ie_i (i = 1,2,..., n) или

А(е_i) = a_1ie₁ + a_2ie₂ + …+a_nie_n = _ie_i ,

Осюда a_ij =0, если ij, и a_ii = _i. Таким образом, матрица оператора А в базисе состоящем из его собственных векторов является диагональной и имеет вид:

A = .

Верно и обратное: если матрица А линейного оператора А в некотором базисе является диагональной, то все векторы этого базиса — собственные векторы оператора А.