Размерность и базис векторного пространства

Вектор а_m называют линейной комбинацией векторов a₁, а₂ ,..., а_m векторного пространства R, если его можно представить в виде суммы произведений этих векторов на некоторые действительные числа ₁,₂,…,_m :

a_m=₁a₁+₂a₂+…+_m-1a_m-1,

Векторы а₁, а₂ ,…, а_m векторного пространства R называют линейно зависимыми, если существуют такие числа ₁,₂,…,_m , не равные одновременно нулю, что

₁a₁+₂a₂+…+_ma_m = 0

Если таких чисел не существует, то векторы a₁, а₂ ,..., а_m называют линейно независимыми.

Если векторы а₁, а₂ ,…, а_m линейно зависимы, то по крайней мере один из них линейно выражается через остальные. Если же один из векторов выражается линейно через остальные, то в совокупности все эти векторы линейно зависимы.

Если среди векторов a₁, а₂ ,..., а_m имеется хотя бы один нулевой вектор, то эти векторы линейно зависимы, так как мы взять коэффициент  при этом векторе (векторах) отличным от нуля. Если часть векторов a₁, а₂ ,..., а_m являются линейно зависимыми, то и все эти векторы — линейно зависимые

Линейное пространство R называется п-мерным, если в нем существует п линейно независимых векторов, а любой набор из (п+1)-го вектора является зависимыми. То есть размерность пространства п — это максимальное число линейно независимых векторов этого пространчтва. Пространство R размерности п. обозначают символом R^п.

Любая совокупность п линейно независимых векторов пространства R^п называется его базисом.

Теорема. Каждый вектор х линейного пространства R можно представить, и притом единственным способом, в виде линейной комбинации векторов базиса.

Пусть векторы e₁,e₂,…,e_n образуют произвольный базис пространства R^п. Так как любые из (п+1) векторов n-мерного пространства R зависимы, то будут зависимы векторы e₁,e₂,…,e_n и вектор х. Тогда существуют такие не равные одновременно нулю числа ₁,₂,…,_n, , что

₁e₁+₂e₂+…+_ne_n+x = 0

При этом 0, ибо в противном случае, если=0 а хотя бы одно из чисел ₁,₂,…,_n было бы отлично от нуля, то векторы e₁,e₂,…,e_n были бы линейно зависимы. Следовательно,

, или

(1)

где x_i =(i = 1,2,…,n).

Это выражение x через e₁,e₂,…,e_n единственное, так как если допустить какое-либо другое выражение, например,

x = y₁e₁+y₂e₂+…+y_ne_n,

то, вычитая из него почленно (9), получим

(y₁ - x₁)e₁+(y₂ - x₂)e₂+…+(y_n - x_n)e_n = 0,

откуда из условия линейной независимости векторов e₁,e₂,…,e_n следует, что

y₁ - x₁=y₂ - x₂=…=y_n - x_n = 0

или y₁=x₁,y₂=x₂,…,y_n=x_n.

Равенство (1) называется разложением вектора х по базису e₁,e₂,…,e_n , а числа x₁,x₂,…,x_n — координатами вектора х относительно этого базиса. В силу единственности разложения каждый вектор однозначно может быть определен координатами в некотором базисе.

Переход к новому базису

Пусть в пространстве R имеются два базиса: старый e₁,e₂,…,e_n и новый e₁*,e₂*,…,e_n*. Каждый из векторов нового базиса можно выразить в виде линейной комбинации векторов старого базиса:

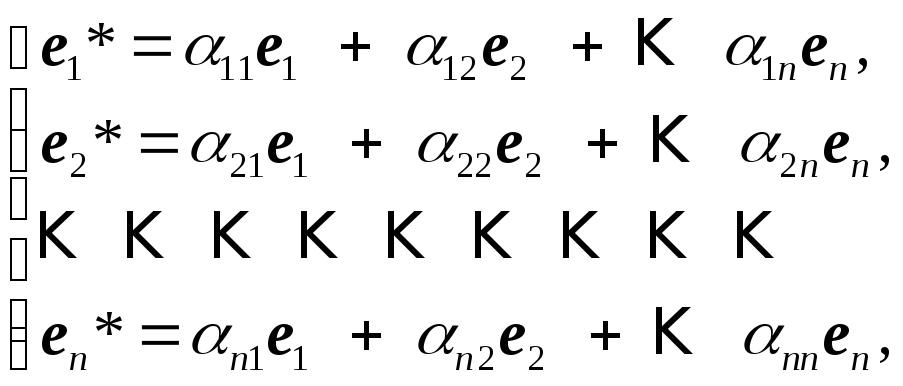(1)

Таким образом переход от старого базиса e₁,e₂,…,e_n к новому e₁*,e₂*,…,e_n* задается матрицей перехода А = (а_ij)(i,j = 1,2,...,n). Эта матрица неособая, так как в противном случае векторы базиса оказались бы линейно зависимыми. Переход от нового базиса e₁*,e₂*,…,e_n* к старому e₁,e₂,…,e_n осуществляется с помощью обратной матрицы А^–1.

Найдем теперь зависимость между координатами вектора в разных базисах. Пусть вектор х имеет координаты (x₁,x₂,…,x_n) относительно старого базиса и координаты (x₁*,x₂*,…,x_n*) относительно нового базиса, т.е.

x = x₁*e₁* + x₂*e₂* +…+ x_n*e_n* = x₁e₁ + x₂e₂ +…+ x_ne_n (2)

Подставив значения e₁*,e₂*,…,e_n* из системы (1) в левую часть равенства (2) получим:

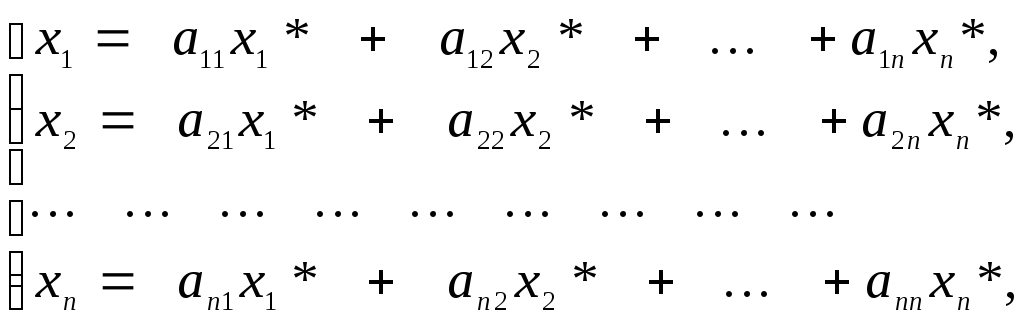
или в матричной форме

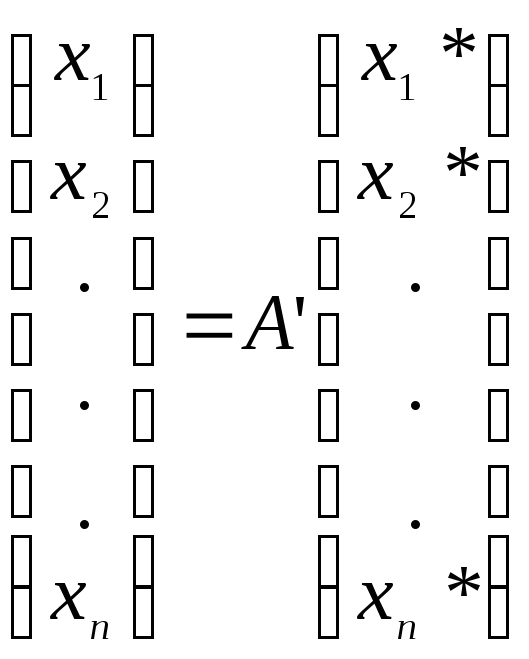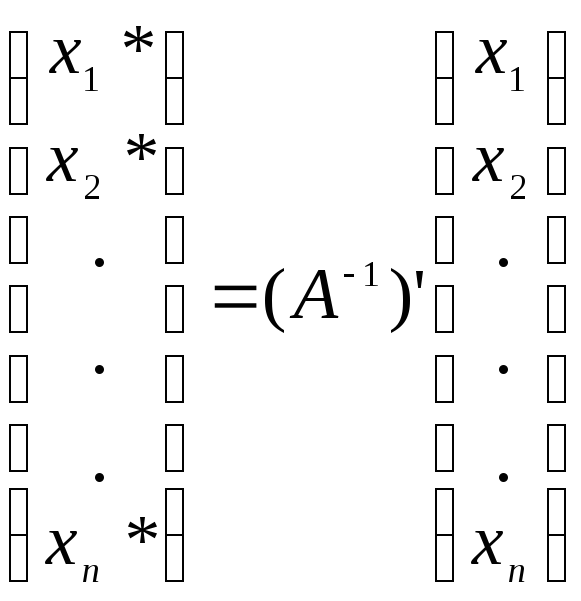или (3)

где А’ и (А^–1)’ — это транспонированные матрицы А и А^–1.