Обратная матрица и алгоритм ее вычисления.

Матрица называетсяобратной по отношению к матрице , если выполняются равенства

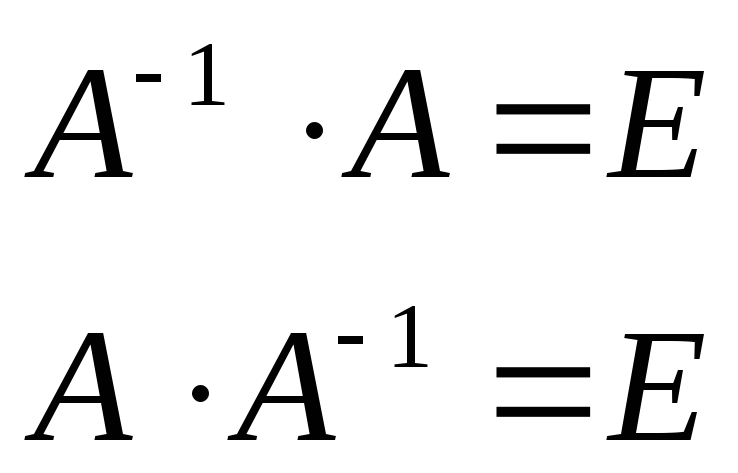
Прямая и обратная матрицы, как и единичная матрица , являются квадратными.

Матрица называетсявырожденной или особой, если ее определитель . В противном случаематрицуназываютневырожденной или неособой.

Необходимое и достаточное условие существования обратной матрицы дает следующая теорема:

Теорема: Обратная матрица существует и является единственной тогда и только тогда, когда матрицане вырождена, т.е..

Необходимость: Пусть существует. Тогда, по определению,

.

По свойству определителя произведения двух матриц имеем

.

Следовательно, .

Достаточность: Пусть - не вырождена, т.е.. Введем так называемуюприсоединенную квадратную матрицу , составленную из алгебраических дополнений, элементов транспонированной матрицы. Элементами присоединенной матрицы будут

.

Умножим теперь на:

.

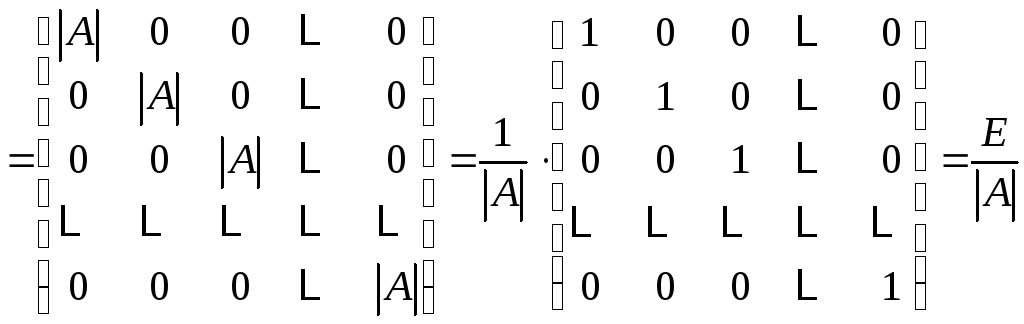Таким образом,

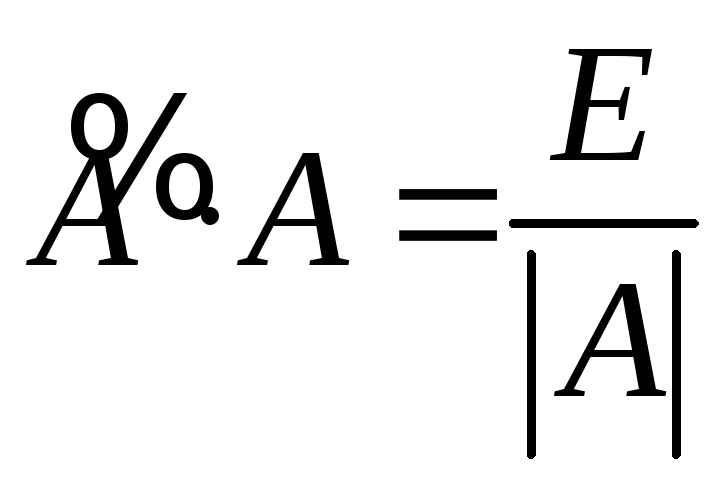или ,

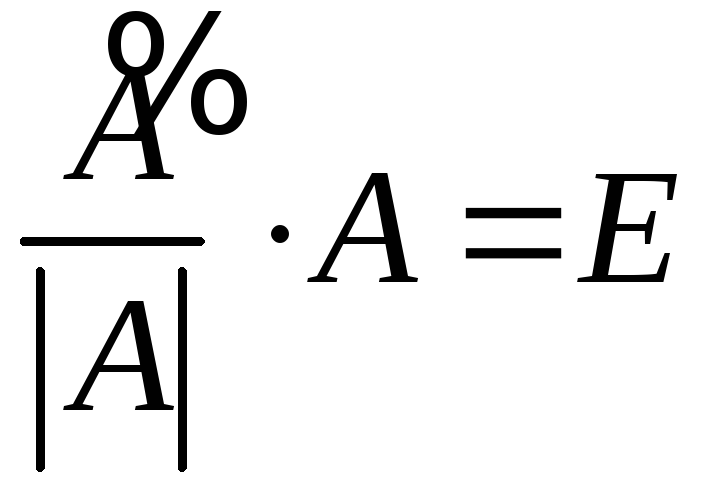поэтому можно принять за .

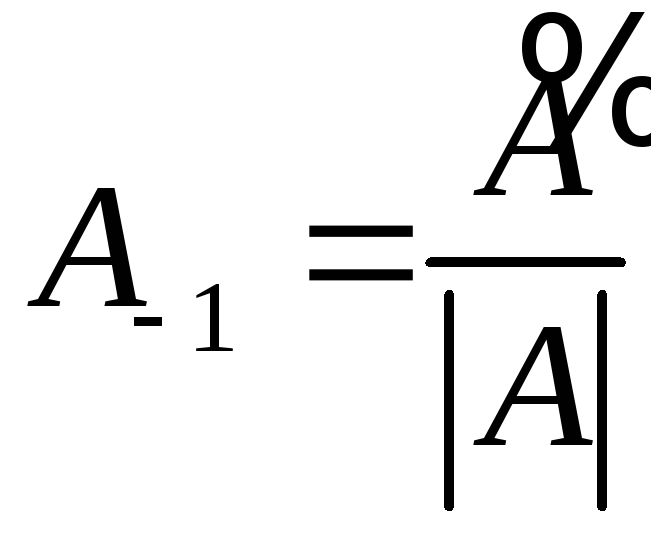Алгоритм нахождения .

1. Вычислить определитель

2. Транспонировать матрицу (найти).

3. Вычислить алгебраические дополнения для всех элементов матрицы -и составить сопряженную матрицу.

4. Разделить матрицу на, т.е. найти

.

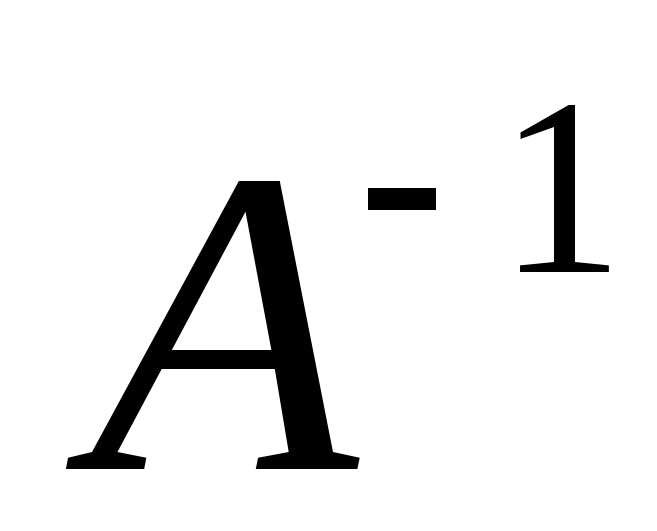
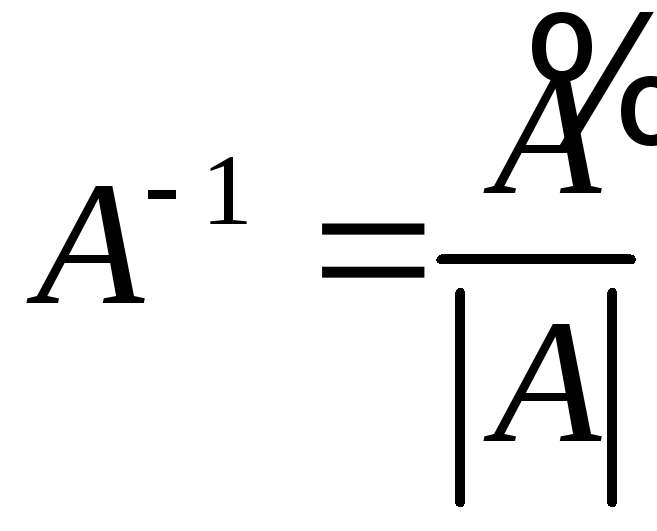5. Выполнить проверку правильности вычислений

.

Понятие о ранге матрицы

Пусть дана произвольная матрица . Из элементов этой матрицы вычеркиванием строк и (или) столбцов можно получить множество квадратных матриц размерностьюот 1 до наименьшего из значенийи:

.

Определители этих квадратных матриц называют минорами матрицы соответствующего порядка.

Рангом матрицы называют наивысший порядок отличного от нуля минора, полученного из матрицывычеркиванием строк и (или) столбцов. Для обозначения ранга матрицы А используются символы

Элементарными преобразованиями матрицы называют следующие операции:

1. Отбрасывание нулевых строк и (или) столбцов.

2. Умножение элементов строки или столбца на отличный от нуля скаляр.

3. Перестановка строк или столбцов.

4. Прибавление к строке (столбцу) линейной комбинации других строк (столбцов).

5. Транспонирование матрицы.

Теорема. Элементарные преобразования не изменяют ранг матрицы.

Элементарные преобразования позволяют привести матрицу (или) к ступенчатому виду:

,

при котором и, где.

Очевидно, что ранг ступенчатой матрицы равен , так как по крайней мере один минор-го порядка в левой части матрицы равен произведению ненулевых диагональных элементов и, следовательно, отличен от нуля.

Ранг суммы матриц подчиняется неравенствам:

Ранг произведения нане превосходит наименьшего из рангов матрици:

.

В частности, если и- квадратные матрицы и определитель, то

.

Отметим также, что

.

Пусть задана произвольная матрица :

.

Каждую строку этой матрицы можно представить матрицей-строкой:

.

Арифметические операции над матрицами-строками выполняются по общим для матриц правилам. Например

,

.

Используя введенные обозначения для строк матрицы , мы можем представить ее в виде матрицы-столбца

,

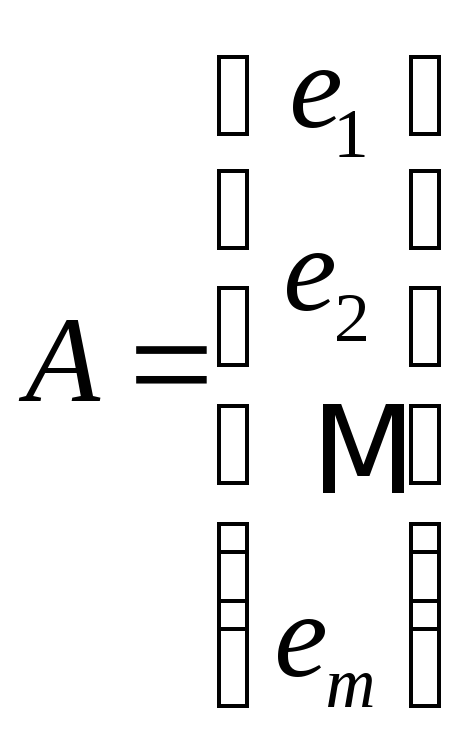в которой элементами служат, в свою очередь, матрицы-строки .

С помощью введенных обозначений уточним понятие линейной зависимости (или независимости), а также линейной комбинации строк матрицы.

Говорят, что строка является линейной комбинацией строк, например,, если выполняется равенство

,

в котором - произвольные числа. В частности, нулевая строка всегда есть линейная комбинация всех остальных, если положить все.

Говорят, что строки линейно-зависимы, если существуют не равные нулю одновременно числатакие, что

.

Допустим, что . Тогда

или

,

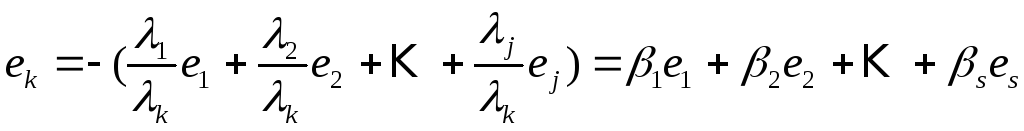где 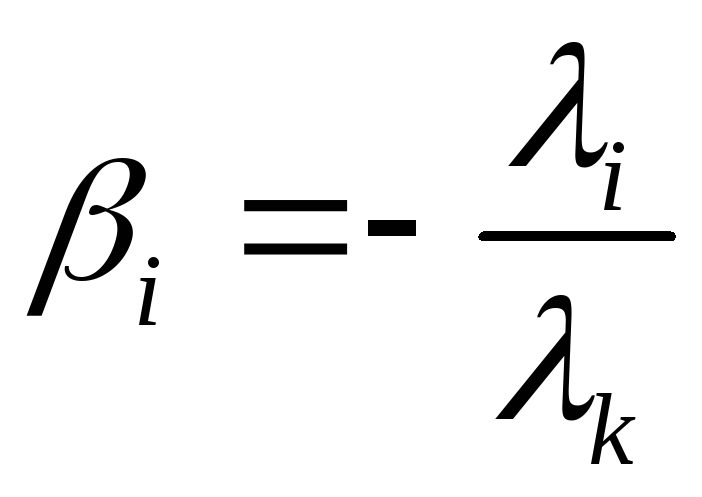,,, т.к.не присутствует в правой части.

Другими словами, если строки линейно-зависимы, то мы всегда можем представить хотя бы одну из них в виде линейной комбинации остальных. Если же указанные строки линейно-независимы, то их линейная комбинация может быть равна нулю только в том случае, когда все_i.

Теорема: Ранг матрицы равен максимальному числу ее линейно-независимых строк (или столбцов), через которые выражаются все ее остальные строки (столбцы).

Доказательство: Пусть . Тогда существует хотя бы один ненулевой минор-го порядка. Не нарушая общности, будем считать, что он расположен в левом верхнем углу:

.

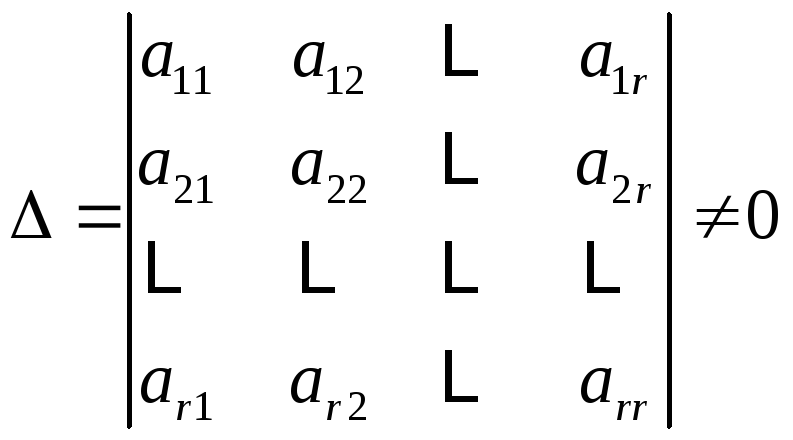Тогда строки - линейно-независимы. Проведем доказательство от противного. Пусть- линейная комбинация остальных строк, т.е.

.

Вычтем теперь из , затем,…, и, наконец,. В результате получими след, что противоречит условию теоремы.

Следовательно, - линейно-независимы. Эти строки, как и исходный минор-го порядка называютбазисными.

Покажем теперь. Что любая небазисная строка матрицы линейно-зависима, т.е. линейно выражается через базисные.

Рассмотрим минор -го порядка, полученный добавлением-той строки и-того столбца к минору порядка:

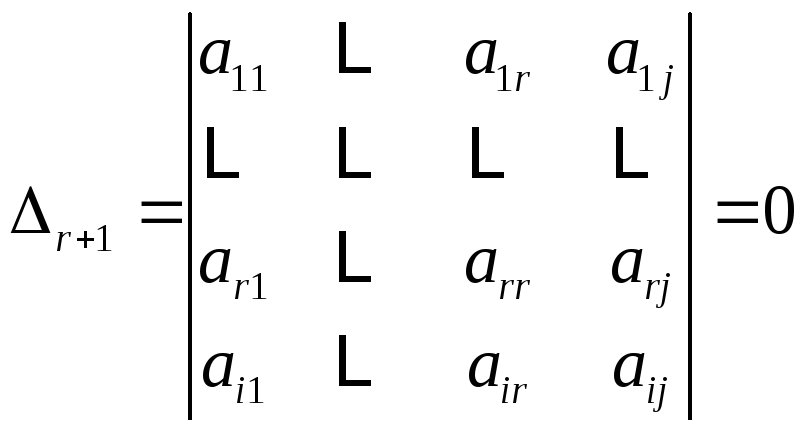, и.

Разложим теперь этот минор по элементам последнего столбца:

, т.к. это базисный минор порядка . Поэтому мы можем разделить последнее равенство наи выразить из него элемент:

.

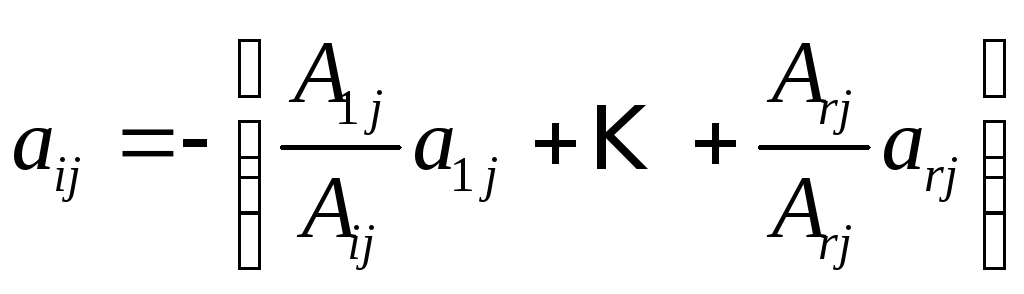Отсюда видно, что для любого иэлементы-той строки линейно выражаются через соответствующие элементы строк, т.е. Она является их линейной комбинацией.