Решение однородных систем линейных уравнений

Однородная система всегда совместна и имеет тривиальное решение. Для существования нетривиального решения необходимо, чтобы ранг матрицыбыл меньше числа неизвестных:

.

Фундаментальной системой решений однородной системы называют систему решений в виде векторов-столбцов, которые соответствуют каноническому базису, т.е. базису, в котором произвольные постоянныепоочередно полагаются равными единице, тогда как остальные приравниваются нулю.

Тогда общее решение однородной системы имеет вид:

,

где - произвольные постоянные. Другими словами, общее решение есть линейная комбинация фундаментальной системы решений.

Таким образом, базисные решения могут быть получены из общего решения, если свободным неизвестным поочередно придавать значение единицы, полагая все остальные равные нулю.

Пример. Найдем решение системы

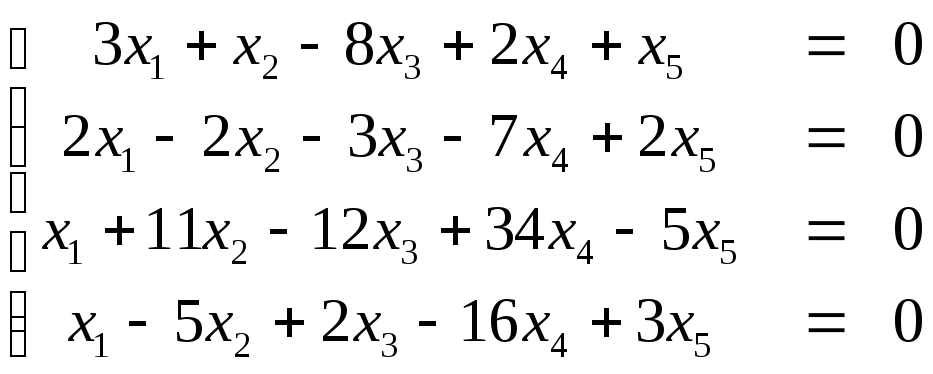
Примем , тогда получим решение в виде:

Построим теперь фундаментальную систему решений:

.

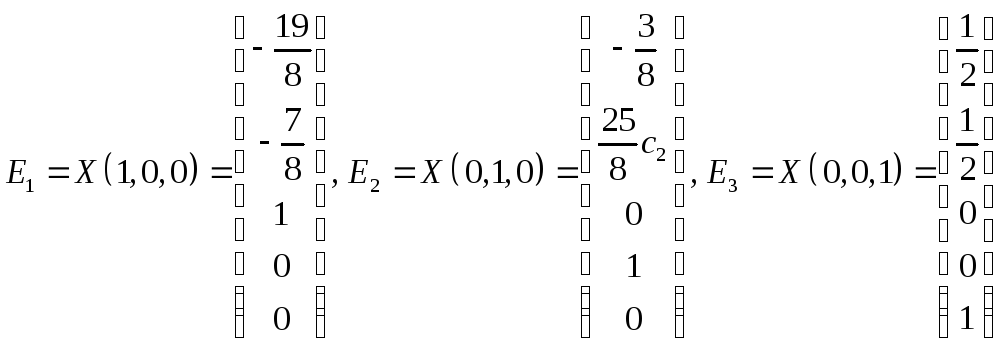Общее решение запишется в виде:

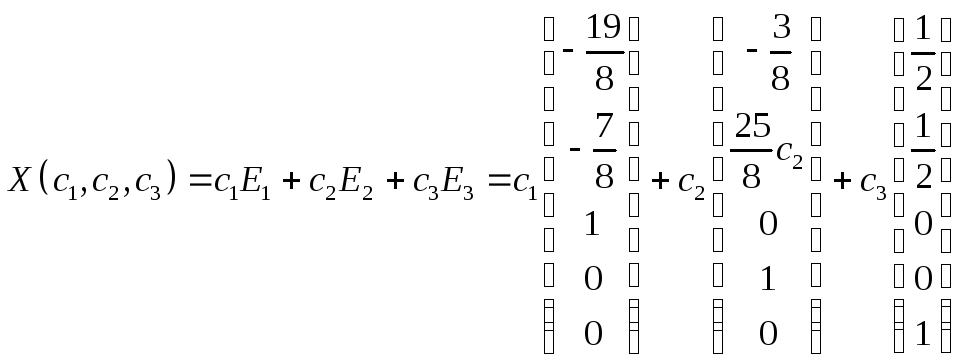
Решения системы однородных линейных уравнений имеют свойства:

1. Если 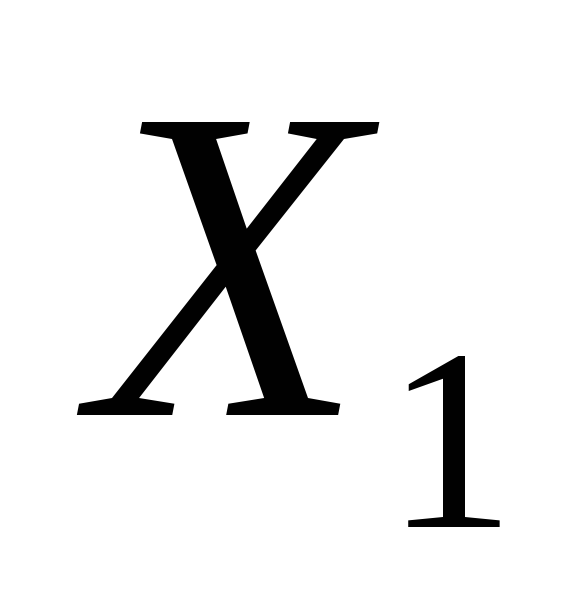- решение системы, то и- также решение.

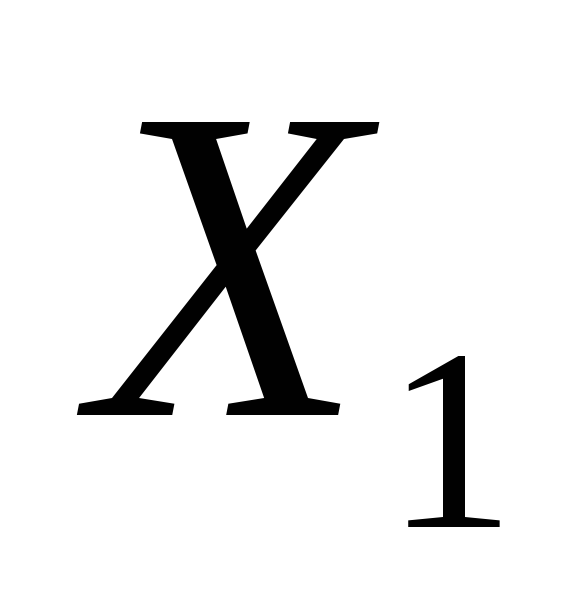2. Если и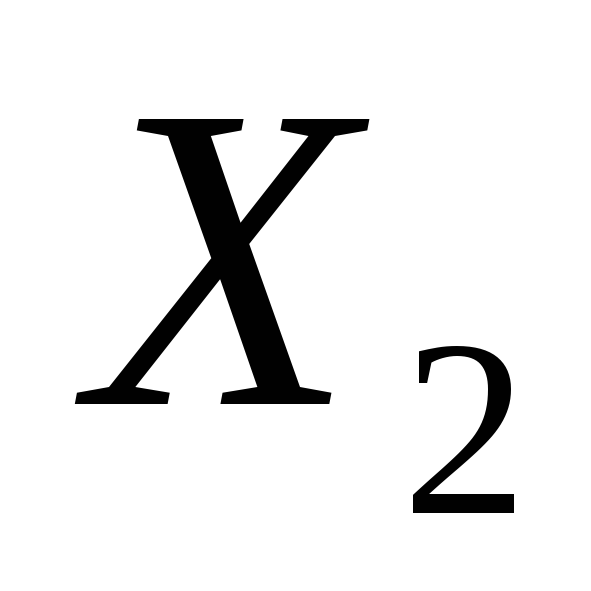- решения системы, то и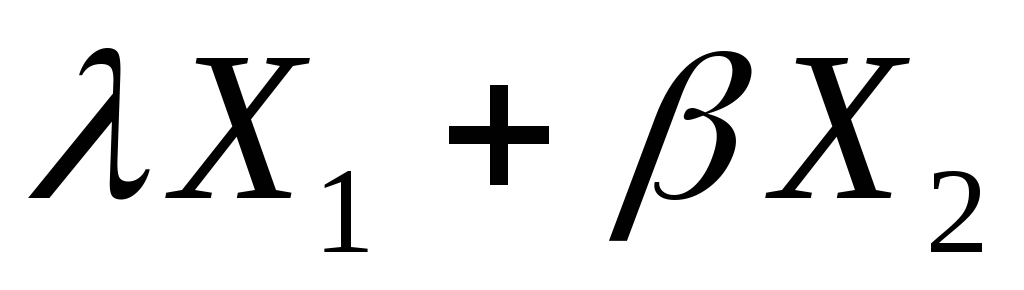- также решение.

Другими словами, любая линейная комбинация решений однородной системы есть опять решение.

Решение систем линейных уравнений методом Гаусса

Решение систем линейных уравнений интересует математиков несколько столетий. Первые результаты были получены в XVIII веке. В 1750 г. Г.Крамер (1704 –1752) опубликовал свои труды по детерминантам квадратных матриц и предложил алгоритм нахождения обратной матрицы. В 1809 г. Гаусс изложил новый метод решения, известный как метод исключения.

Метод Гаусса, или метод последовательного исключения неизвестных, заключается в том, что с помощью элементарных преобразований система уравнений приводится к равносильной системе ступенчатого (или треугольного) вида. Такие системы позволяют последовательно находить все неизвестные в определенном порядке.

Предположим, что в системе (1) (что всегда возможно).

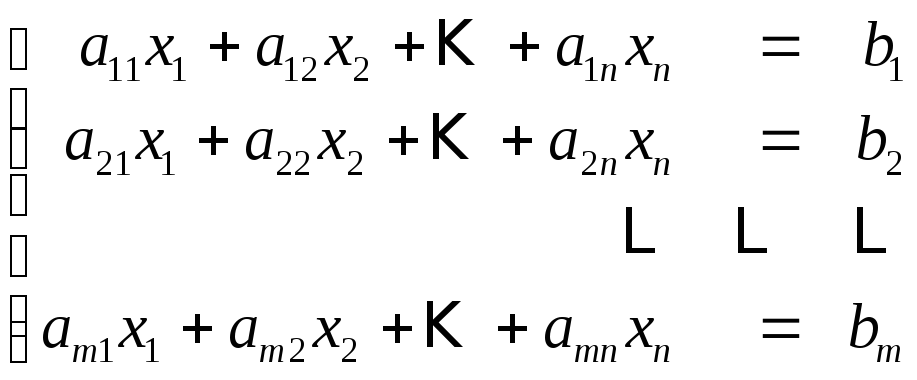(1)

Умножая поочередно первое уравнение на так называемые подходящие числа

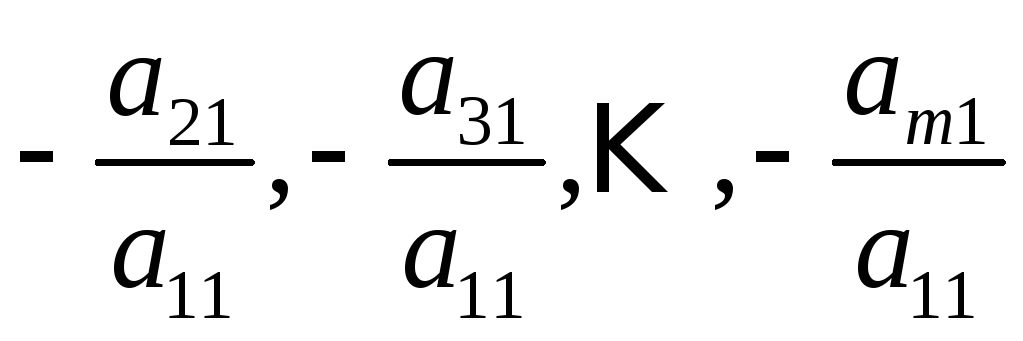
и складывая результат умножения с соответствующими уравнениями системы, мы получим эквивалентную систему, в которой во всех уравнениях, кроме первого, будет отсутствовать неизвестная х₁

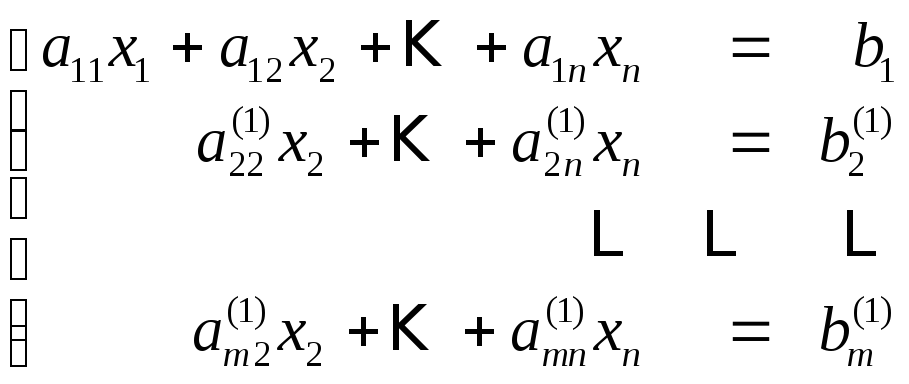(2)

Умножим теперь второе уравнение системы (2) на подходящие числа, полагая, что

,

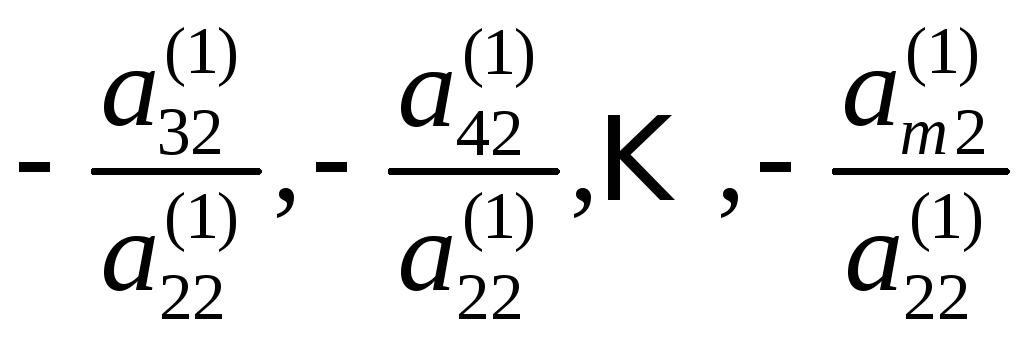и складывая его с нижестоящими, исключим переменную из всех уравнений, начиная с третьего.

Продолжая этот процесс, после шага мы получим:

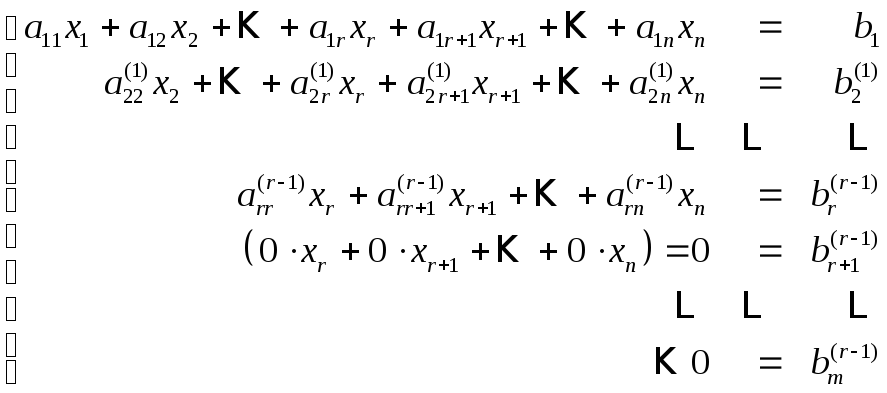(3)

Если хотя бы одно из чисел не равно нулю, то соответствующее равенство противоречиво и система (1) несовместна. Обратно, для любой совместной системы числаравны нулю. Число- это ни что иное, как ранг матрицы системы (1).

Переход от системы (1) к (3) называется прямым ходом метода Гаусса, а нахождение неизвестных из (3) – обратным ходом.

Замечание: Преобразования удобнее производить не с самими уравнениями, а с расширенной матрицей системы (1).

Пример. Найдем решение системы

.

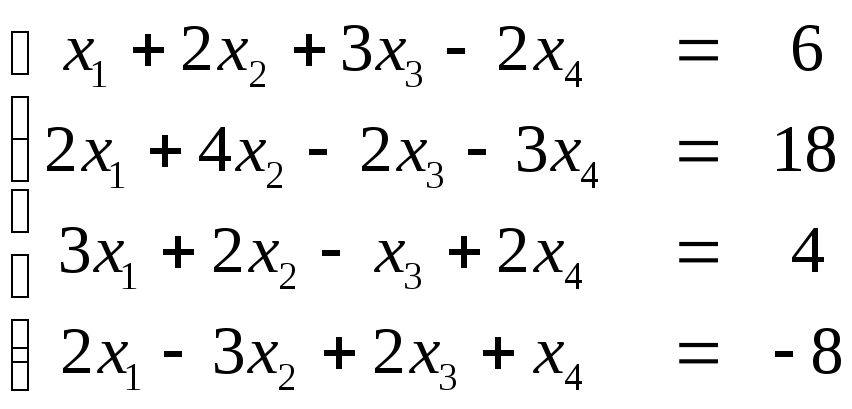Запишем расширенную матрицу системы:

.

Прибавим к строкам 2,3,4 первую, умноженную на (-2), (-3), (-2) соответственно:

.

Поменяем строки 2 и 3 местами, затем в получившейся матрице добавим к строке 4 строку 2, умноженную на :

.

Прибавим к строке 4 строку 3, умноженную на :

.

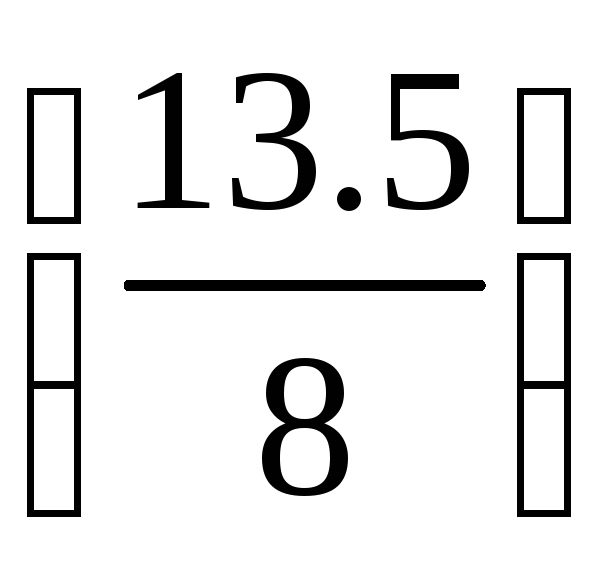Очевидно, что , следовательно, система совместна. Из полученной системы уравнений

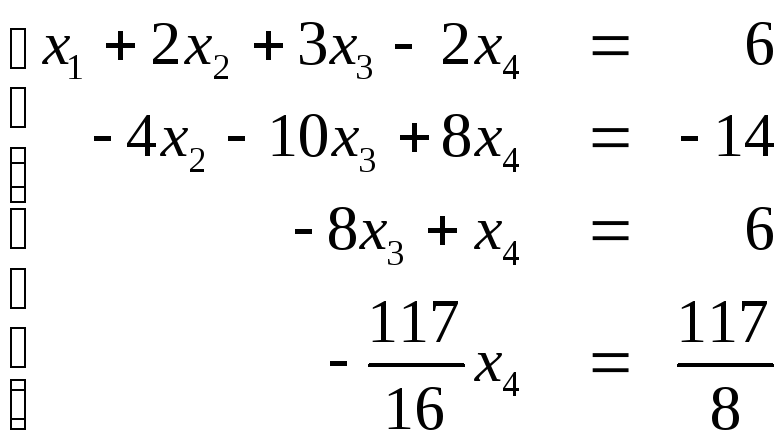
находим решение обратной подстановкой:

, ,,.

Пример 2. Найти решение системы:

.

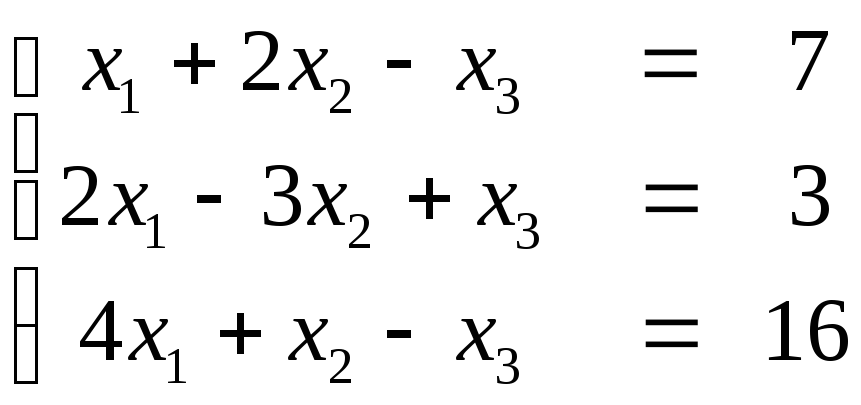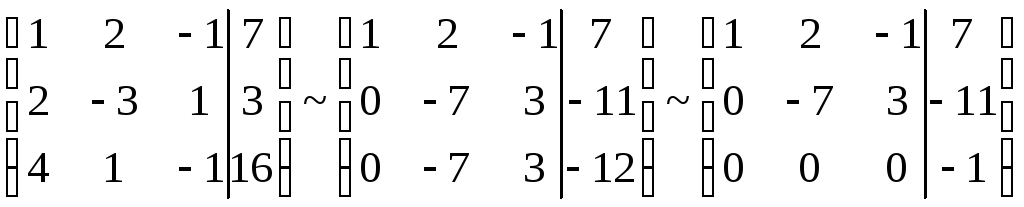
Очевидно, что система несовместна, т.к. , а.

Достоинства метода Гаусса:

1. Менее трудоемкий, чем метод Крамера.

2. Однозначно устанавливает совместность системы и позволяет найти решение.

3. Дает возможность определить ранг любых матриц.