Квадратичные формы

Квадратичной формой L(x₁,x₂,…,x_n) от п переменных называется сумма, каждый член которой является квадратом одной из переменных, либо произведением двух разных переменных, взятых с некоторыми коэффициентом:

L(x₁,x₂,…,x_n) = . (4)

Пусть коэффициенты квадратичной формы a_ij— действительные числа. Причем a_ij=а_ji., то есть матрица симметрична относительно главной диагонали. Матрица А = (a_ij) (i,j = 1,2,...,n), составленная из этих коэффициентов, называется матрицей квадратичной формы.

В матричной записи квадратичная форма имеет вид:

L = X 'AX (5)

где Х = (х₁,x₂,...,х_n)' — матрица-столбец переменных. В самом деле :

L(x₁,x₂,…,x_n) = 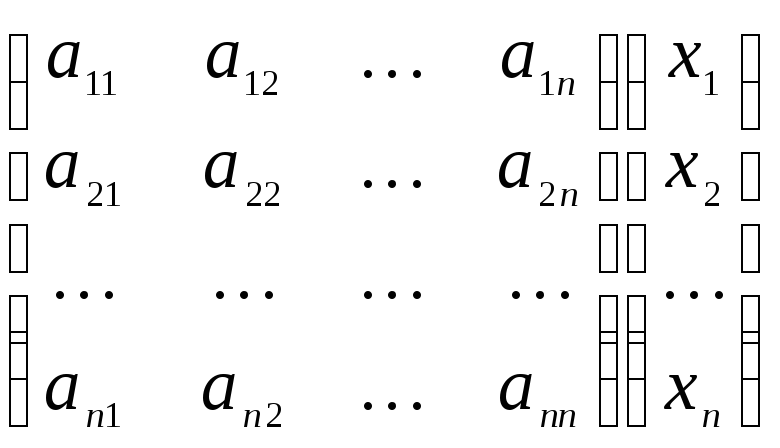=(x₁,x_.2,…,x_n)=

=

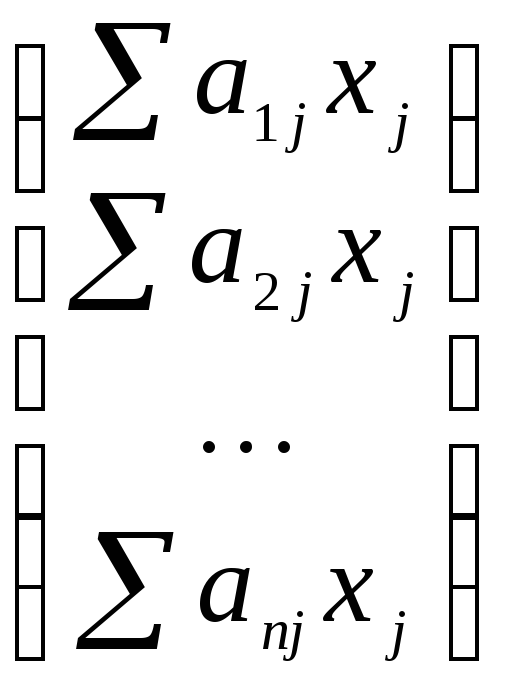Выясним, как изменяется квадратичная форма при невырожденном линейном преобразовании переменных.

Пусть матрицы-столбцы переменных Х = (х₁,х₂,...,x_n)' и Y = (у₁,у₂ ,…,y_n)' связаны линейным соотношением Х = СY, где С = (c_ij) (i,j=1,2,...,n) есть некоторая невырожденная матрица п-го порядка. Тогда квадратичная форма

L = Х'АХ = (С'Y')A(СY) = (Y'С')A(СY) = Y'(С'АС)Y.

Итак, при невырожденном линейном преобразовании Х = СY матрица квадратичной формы принимает вид:

А* =С'АС. (6)

Следует отметить, что при некоторых удачно выбранных линейных преобразованиях вид квадратичной формы можно существенно упростить.

Квадратичная форма L = 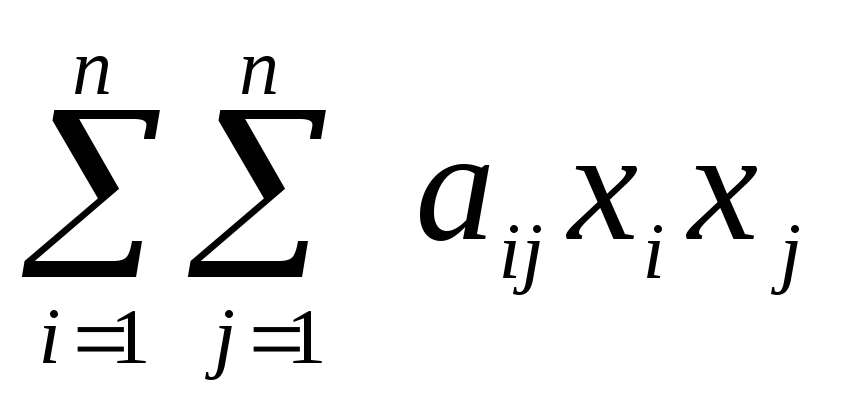называетсяканонической, если все ее коэффициенты a_ij = 0 при ij, то есть ее матрица является диагональной.

L = a₁₁x₁² +a₂₂x₂² +…+a_nnx_n² =

Теорема. Любая квадратичная форма с помощью невырожденного линейного преобразования переменных может быть приведена к каноническому виду.

Канонический вид квадратичной формы не является однозначно определенным, так как одна и та же квадратичная форма может быть приведена к каноническому виду многими способами. Однако полученные различными способами канонические формы обладают рядом общих свойств. Одно из этих свойств сформулируем в виде теоремы.

Закон инерции квадратичных форм. Число слагаемыхс положительными (или отрицательными) коэффициентами квадратичной формы не зависит от способа приведения формы к этому виду.

Следует отметить, что ранг матрицы квадратичной формы, называемый рангом квадратичной формы, равен числу отличных от нуля коэффициентов канонической формы и не меняется при линейных преобразованиях.

Квадратичная форма L(x₁,x₂,…,x_n) называется положительно (отрицательно) определенной, если при всех значениях переменных, из которых хотя бы одно отлично от нуля,

L(x₁,x₂,…,x_n) > 0 (L(x₁,x₂,…,x_n) < 0) .

Так, например, квадратичная форма L₁ = 3x₁² + 4x₂² + 9x₃² является положительно определенной, а форма L₂ = –x₁² + 2х₁x₂ – x₂² — отрицательно определенной.

Теорема. Для того чтобы квадратичная форма L = Х'АХ была положительно (отрицательно) определенной, необходимо и достаточно, чтобы все собственные значения _i матрицы А были положительны (отрицательны).

Модель международной торговли

В качестве примера математической модели экономического процесса, приводящейся к понятию собственного вектора и собственного значения матрицы, рассмотрим линейную модель международной торговли.

Пусть имеется n стран S₁,S₂,…,S_n , национальный доход каждой из которых равен соответственно x₁,x₂,…x_n. Обозначим коэффициентами a_ij долю национального дохода, которую страна S_j тратит на покупку товаров у страны S_i. Будем считать, что весь национальный доход тратится на закупку товаров либо внутри страны, либо на импорт из других стран, т.е.

(j = 1,2,…,n). (1)

Рассмотрим матрицу А = ,

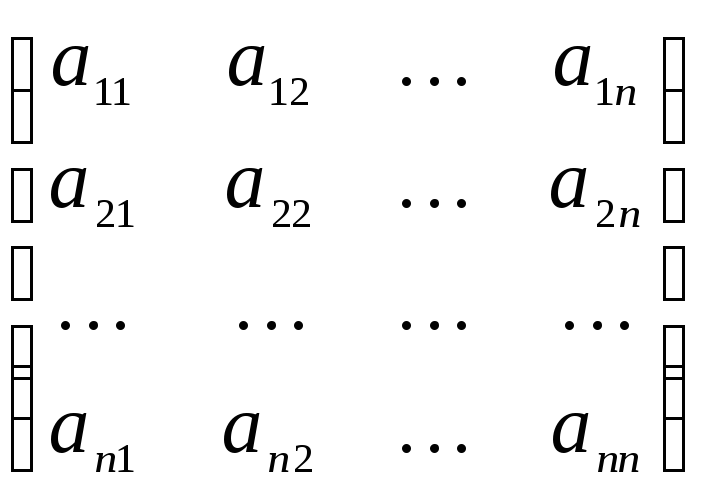которая получила название структурной матрицы торговли. В соответствии с (1) сумма элементов любого столбца матрицы А равна 1.

Для любой страны S_i (i=1,2,...,n) выручка от внутренней и внешней торговли составит:

p_i = a_i1x₁ + a_i2x₂ + … + a_inx_n.

Для сбалансированной торговли необходима бездефицитность торговли каждой страны S_i, т.е. выручка от торговли каждой страны должна быть не меньше ее национального дохода:

p_i x_i (i = 1,2,…,n) .

Если считать, что р_i > x_i, (i = 1,2,...,n), то получаем систему неравенств

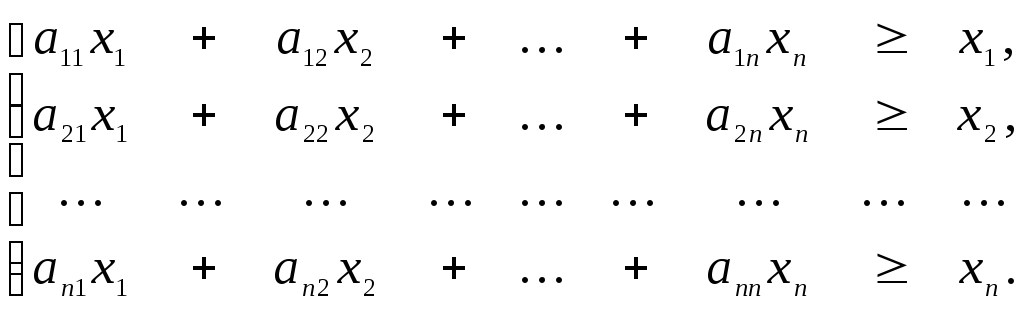(2)

Сложив все неравенства системы (2), получим после группировки

x₁(a₁₁+a_21`+…+a_n1)+x₂(a₁₂+a₂₂+…+a_n2)+…+x_n(a_1n+a_2n+…++a_nn)>x₁+x₂+…+x_n .

Учитывая (1), что выражения в скобках равны 1, мы приходим к противоречивому неравенству

x₁+x₂+…+x_n >x₁+x₂+…+x_n .

Таким образом, неравенство p_ix_i (i=1,2,...,n) невозможно, и условие p_ix_i, принимает вид p_i=x_i (i=1,2,...,n). С экономической точки зрения это означает, что все страны не могут получать прибыль одновременно.

Вводя вектор национальных доходов стран

x = ,

получим уравнение Ax = x, т.е. задача свелась к отысканию собственного вектора матрицы А, отвечающему собственному значению =1.

Пример. Пусть структурная матрица торговли трех стран S₁, S₂ , S₃ имеет вид:

A = .

Найти национальные доходы стран для сбалансированной торговли.

Решение. Собственный вектор х, отвечающий собственному значению  = 1, найдем, решив уравнение (А - Е)х = 0 или систему

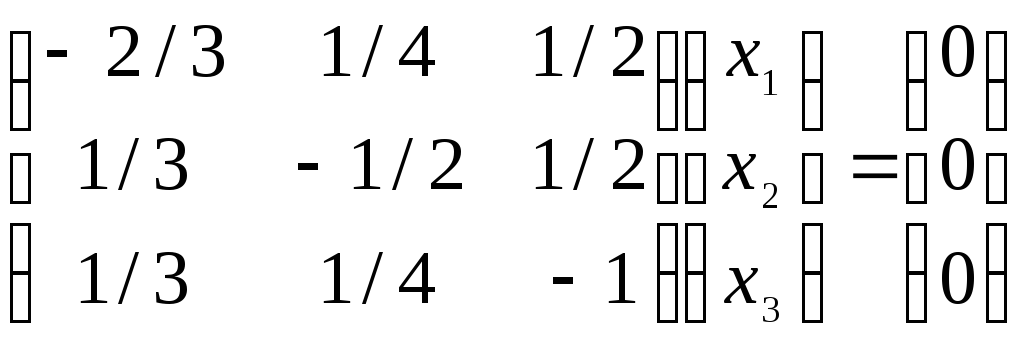
Получим х₁=1,5с, х₂=2с, x₃=с, т.е. x=(1,5с; 2с; с). Этот результат означает, что сбалансированность торговли трех стран достигается при векторе национальных доходов x=(1,5с; 2с; с), то есть при соотношении национальных доходов стран 1,5:2:1 или 3:4:2.