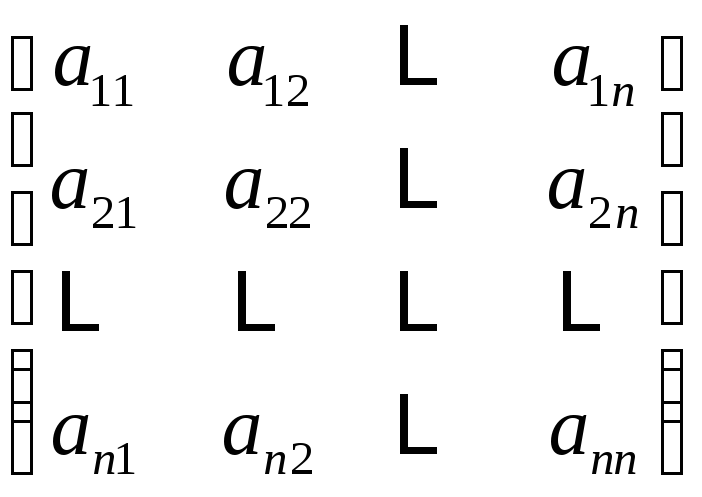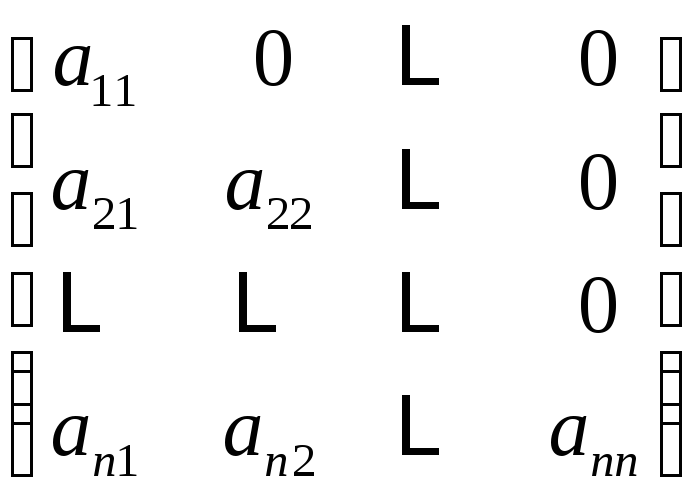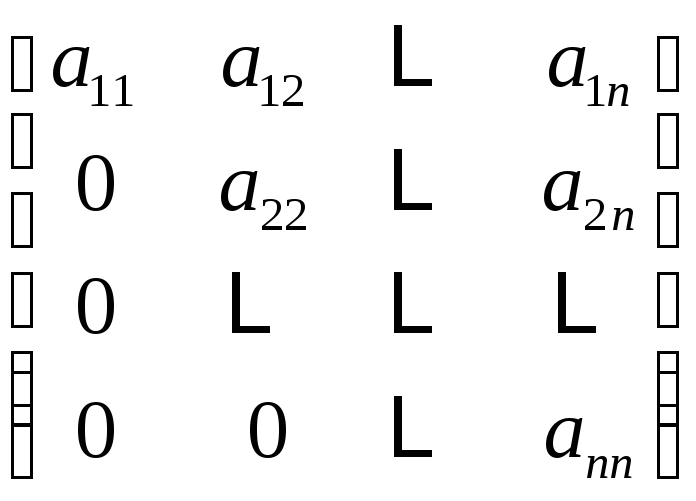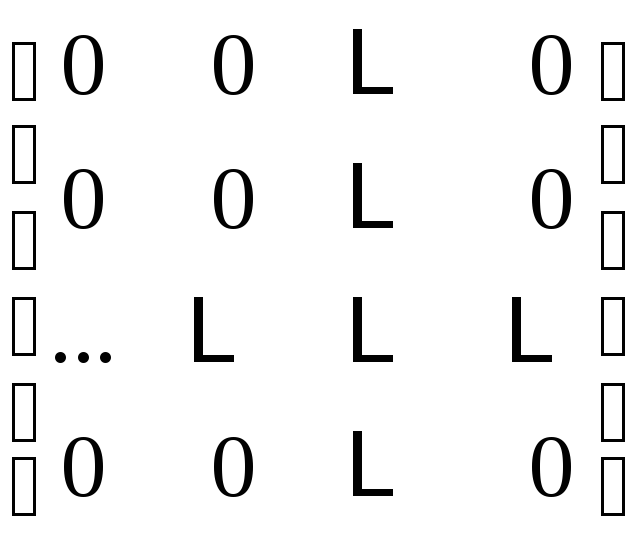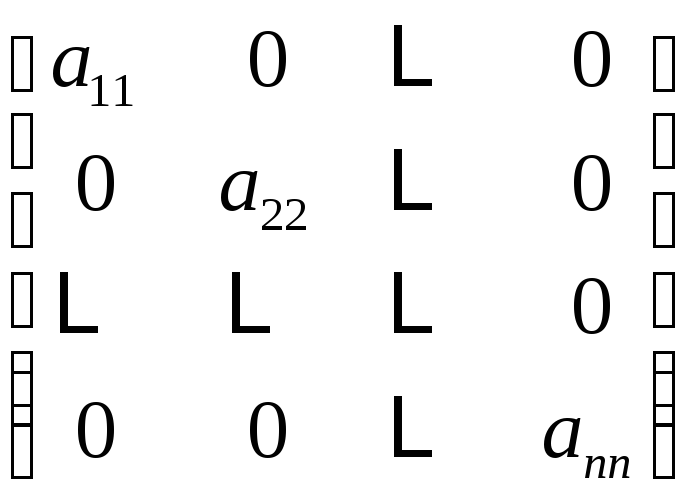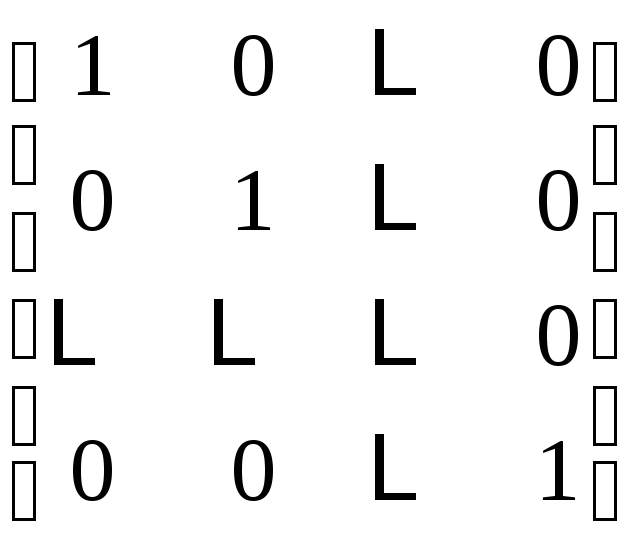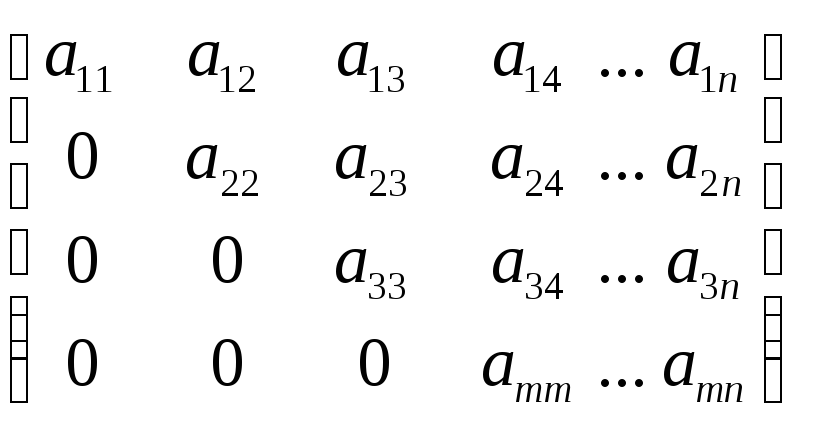Линейная алгебра Матрицы и определители.

Большинство математических моделей в экономике описываются с помощью матриц и матричного исчисления.

Матрица - это прямоугольная таблица, содержащая числа, функции, уравнения или другие математические объекты, расположенные в строках и столбцах.

Объекты, составляющие матрицу, называют ее элементами. Матрицы обозначают заглавными латинскими буквами

а их элементы – строчными.

Символ означает, что матрицаимеетстрок истолбцов,элемент, находящийся на пересечении–й строки и–го столбца.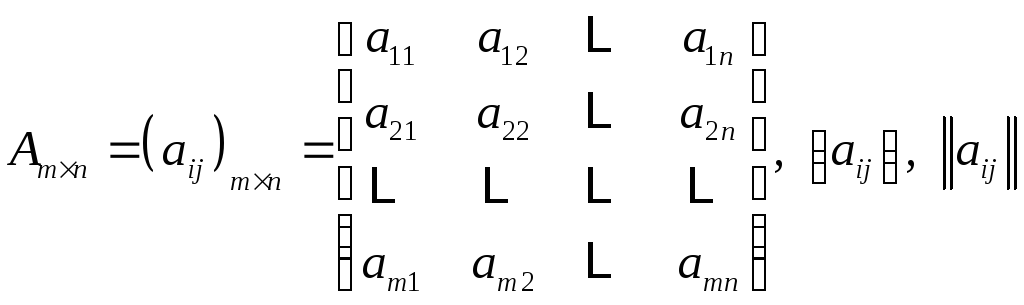

.

_{Говорят, что матрица А равна матрице В: А=В} , если они имеют одинаковую структуру (то есть одинаковое число строк и столбцов) и их соответсвующие элементы тождественно равны , для всех.

Частные виды матриц

На практике довольно часто встречаются матрицы специального вида. Некоторые методы предполагают также преобразования матриц от одного вида к другому. Наиболее часто встречающиеся виды матриц приведены ниже.

	квадратная матрица, число строк n равно числу столбцов n
	матрица-столбец
	матрица-строка
	нижняя треугольная матрица
	верхняя треугольная матрица
	нулевая матрица
	диагональная матрица
Е =	единичная матрица Е (квадратная)
	унитарная матрица
	ступенчатая матрица
( )	Пустая матрица

Элементы матрицы, с равными номерами строк и столбцов, то есть a_ii образуют главную диагональ матрицы.

Операции над матрицами.

1. При умножении матрицы А на скаляр (число), необходимо умножить на это число все элементы матрицы 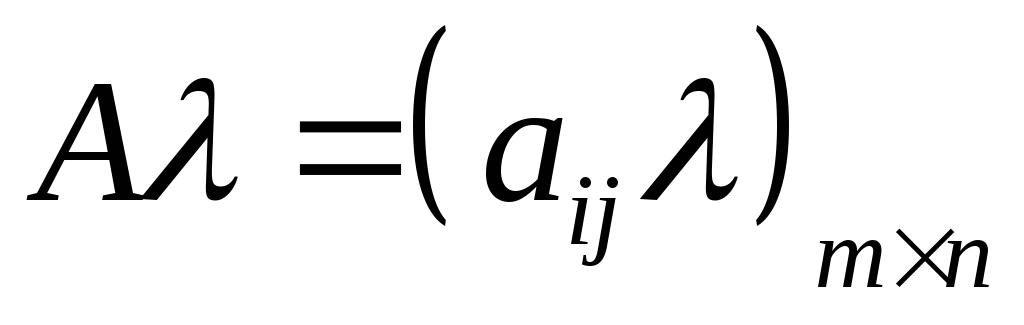. Общий множитель всех элементов можно вынести за знак матрицы.

2. Сложение матрицы и числа,

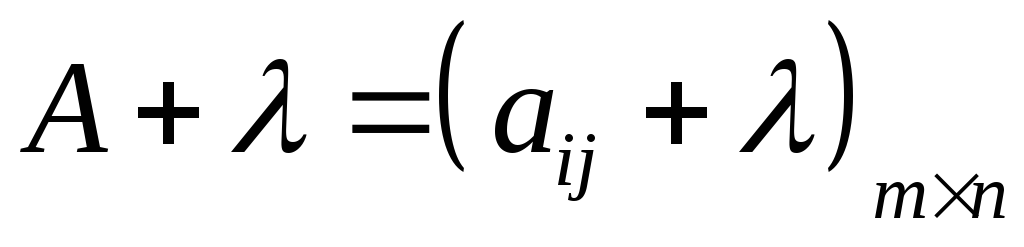
3. Сложение матриц

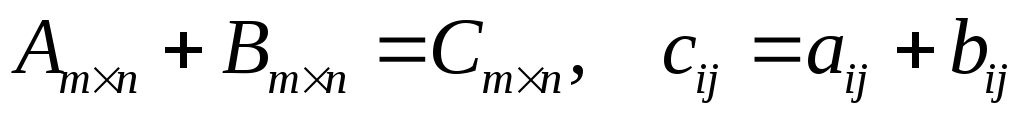
4. Вычитание матриц

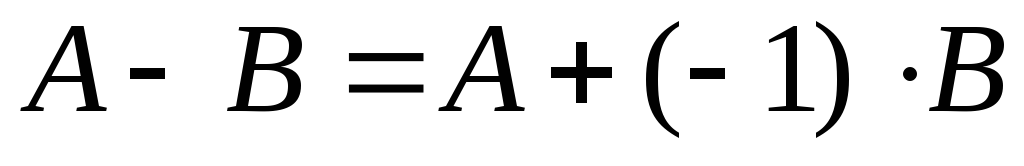
5. Умножение двух матриц возможно только тогда, когда число строк первой равно числу строк второй. Произведением 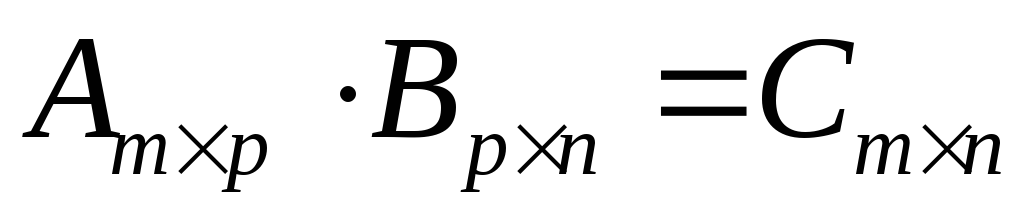, где каждый элемент матрицыС — 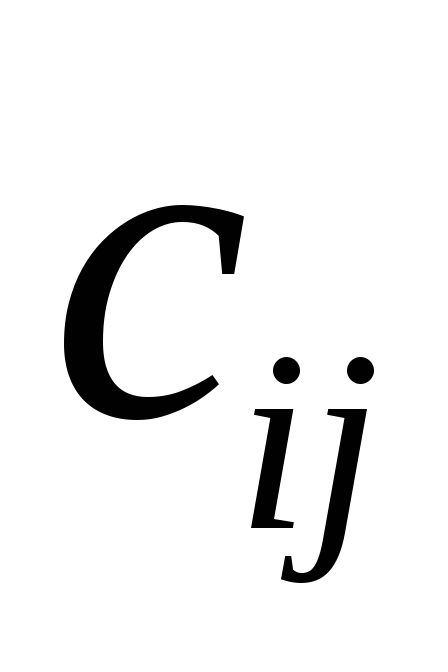есть сумма произведений всех элементов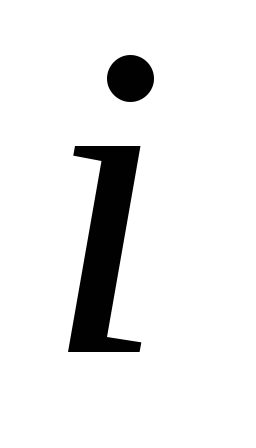–й строкина соответсвующие элементы–го столбца.

.

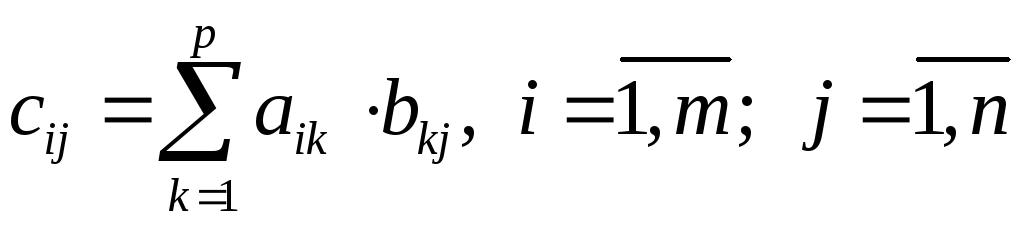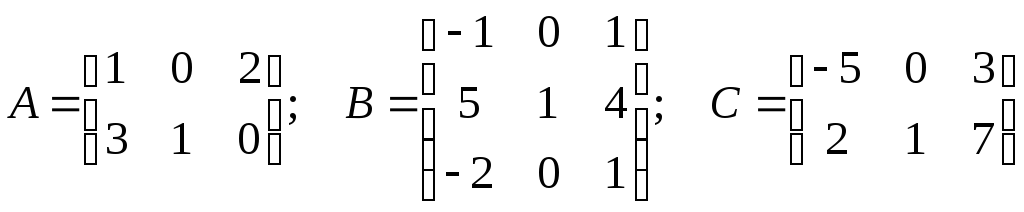
Свойства операций над матрицами

1. 

2. 

3. 

4. 

5. 

6. 

7. 

Специфические свойства оперций

Если произведение матриц – существует, то произведениеможет и не существовать. Вообще говоря,. То есть умножение матриц не коммутативно. Если же, тоиназывают коммутативными. Например, диагональные матрицы одного порядка коммутативны.

Если , то необязательноили. Т.е., произведение ненулевых матриц может дать нулевую матрицу. Например

Операция возведения в степень определена только для квадратных матриц. Если , то

.

По определению полагают , и нетрудно показать, что,. Отметим, что из не следует, что.

Поэлементное возведение в степень А.^m = .

Операция транспонирования матрицы заключается в замене строк матрицы ее столбцами:

,

Например

, .

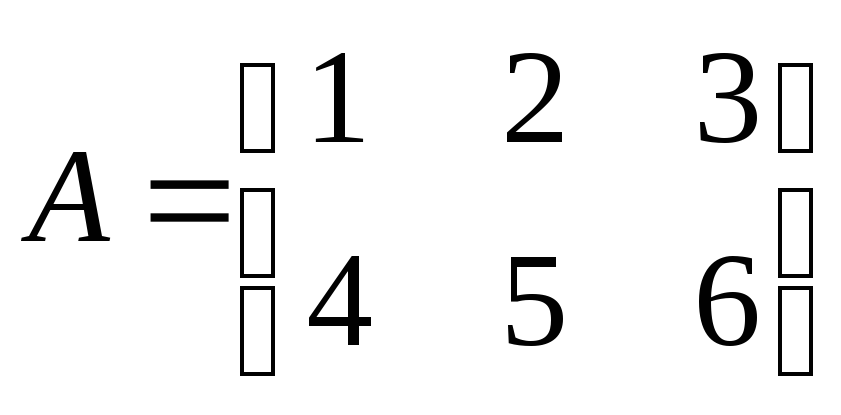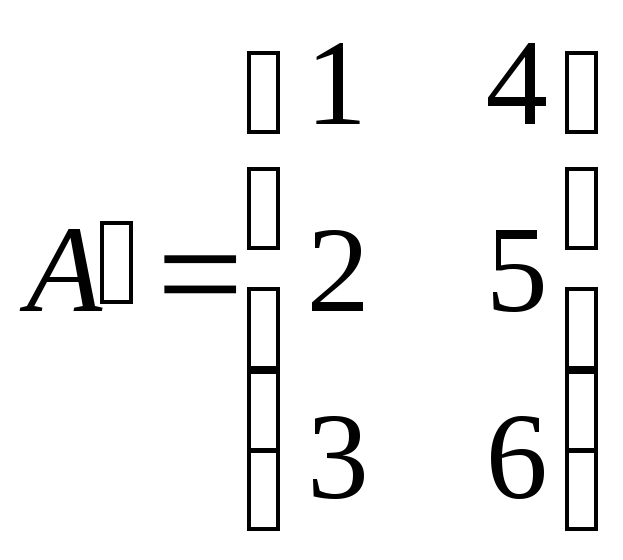Свойства транспонирования:

1. 

2. 

3. 

4. 

Определители и их свойства.

Для квадратных матриц часто используется понятие определителя – числа, которое вычисляется по элементам матрицы с использованием строго определенных правил. Это число является важной характеристикой матрицы и обозначается символами

.

Определителем матрицы является ее элемент.

.

Определитель матрицы 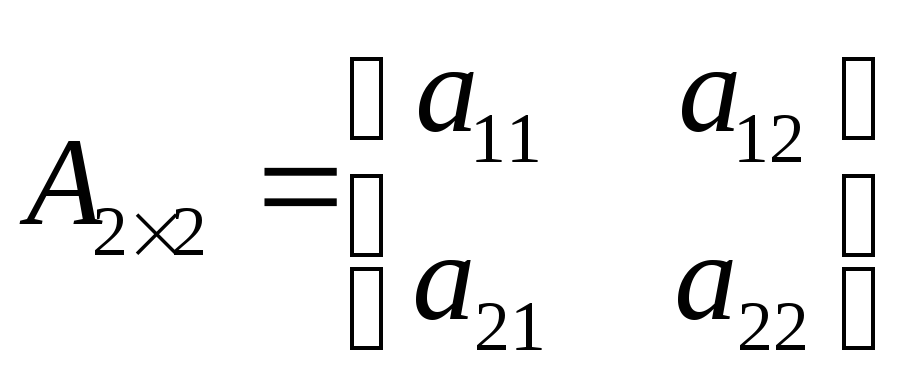вычисляется по правилу:

,

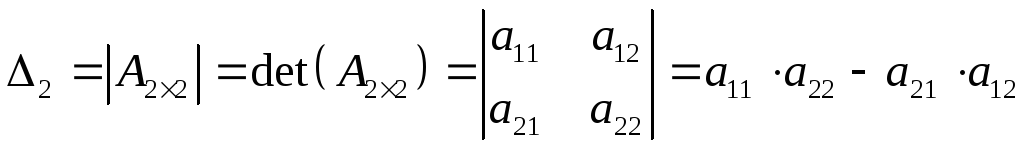т.е., из произведения элементов главной диагонали вычитается произведение элементов дополнительной диагонали.

Для вычисления определителей более высокого порядка () необходимо ввести понятия минора и алгебраического дополнения элемента.

Минором элемента называют определитель, который получают из матрицы, вычеркивая-ю строку и-й столбец.

Рассмотрим матрицу размером:

,

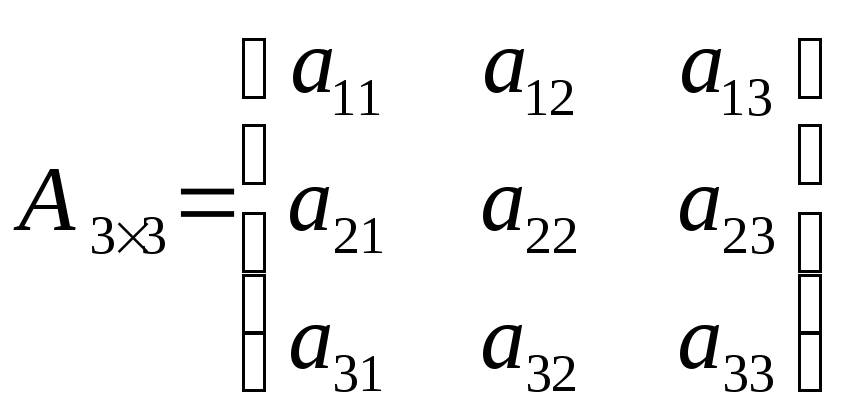тогда, например,

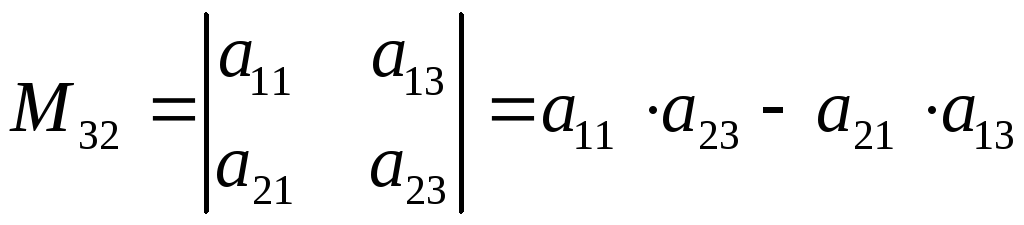
Алгебраическим дополнением элементаназывают его минор, умноженный на.

,

.

Теорема Лапласа: Определитель квадратной матрицы равен сумме произведений элементов любой строки (столбца) на их алгебраические дополнения.

Например, разлагая по элементам первой строки, получим:

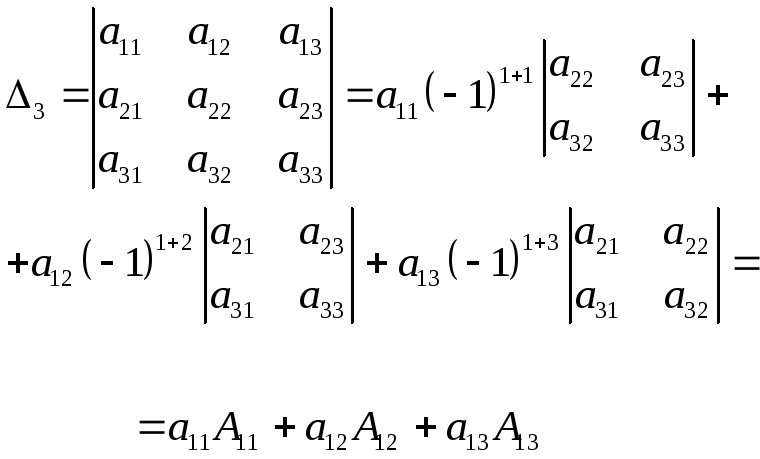
Последняя теорема дает универсальный способ вычисления определителей любого порядка, начиная со второго. В качестве строки (столбца) всегда выбирают тот, в котором имеется наибольшее число нулей. Например, требуется вычислить определитель четвертого порядка

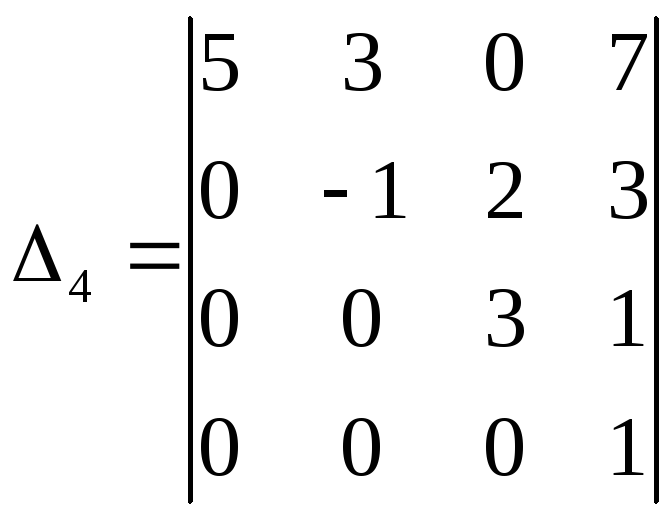
В данном случае можно разложить определитель по первому столбцу:

,

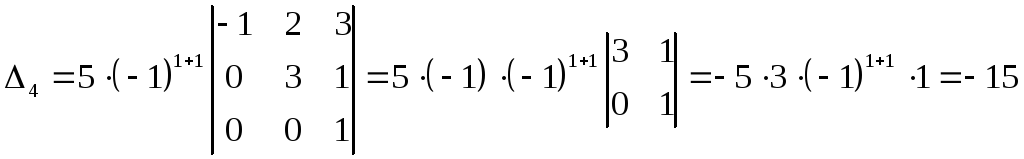или последней строке:

.

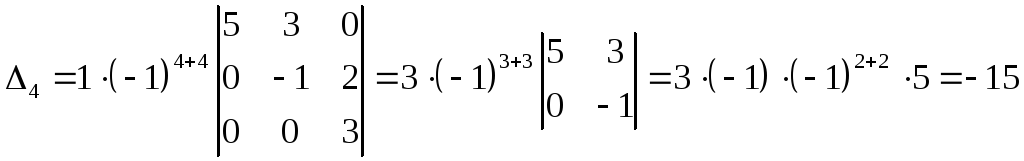Этот пример показывает также, что определитель верхней треугольной матрицы равен произведению ее диагональных элементов. Нетрудно доказать, что этот вывод справедлив для любых треугольных и диагональных матриц.

Теорема Лапласа дает возможность свести вычисление определителя -го порядка к вычислениюопределителей-го порядка и, в конечном итоге, к вычислению определителей второго порядка.