
- •Линейная алгебра Матрицы и определители.
- •Операции над матрицами.
- •Определители и их свойства.
- •Свойства определителей.
- •Обратная матрица и алгоритм ее вычисления.
- •Понятие о ранге матрицы
- •Системы линейных уравнений. Решение и исследование системы трех линейных уравнений с тремя неизвестными.
- •Однородная система трех линейных уравнений с тремя неизвестными.
- •Решение произвольных систем линейных уравнений
- •Решение однородных систем линейных уравнений
- •Решение систем линейных уравнений методом Гаусса
- •Модель многоотраслевой экономики (балансовый метод или модель Леонтьева)
- •Многомерные вектора и векторные пространства
- •Размерность и базис векторного пространства
- •Переход к новому базису
- •Евклидово пространство
- •Линейные операторы
- •В силу линейности оператора Аполучаем
- •Собственные векторы и собственные значения линейного оператора
- •Квадратичные формы
- •Модель международной торговли
Системы линейных уравнений. Решение и исследование системы трех линейных уравнений с тремя неизвестными.
Пусть дана система трех линейных уравнений с тремя неизвестными — x, y, z :
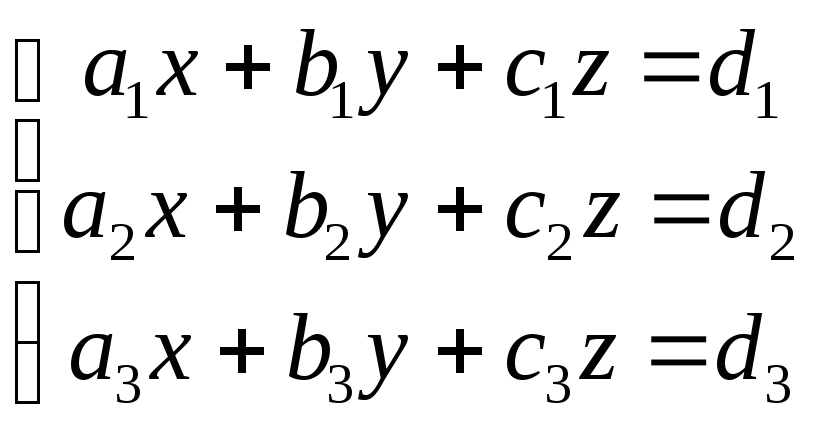 ,
,
![]()
ее главный определитель, составленный из коэффициентов при неизвестных, имеет вид
 .
.
Если
![]() ,
то
,
то![]() ,
,![]() ,
,![]() ,
где
,
где
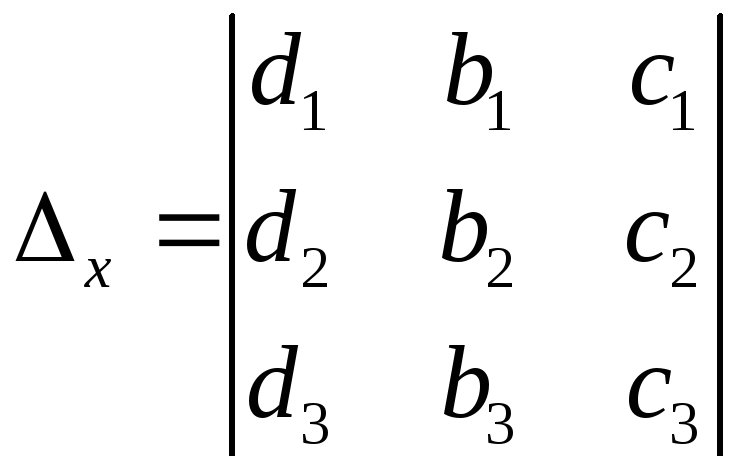 ,
,
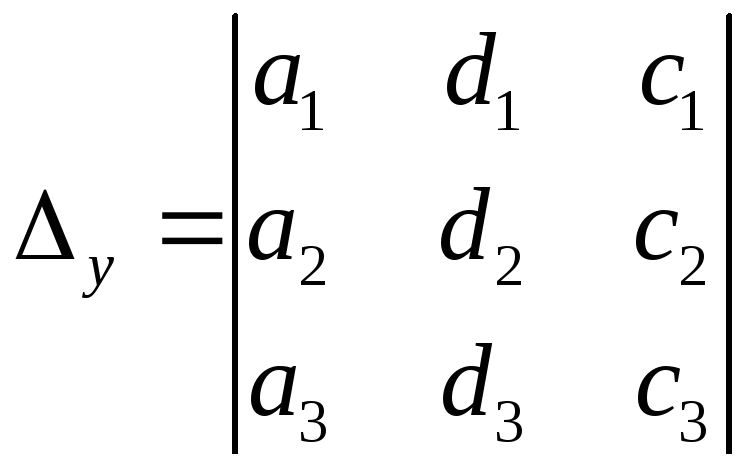 ,
,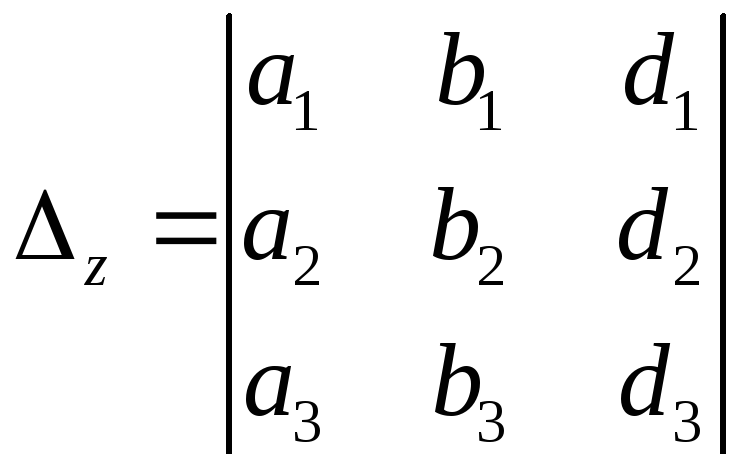 .
.
Пусть
теперь
![]() ,
но есть
,
но есть![]() .
Тогда можно утверждать, что, например,
.
Тогда можно утверждать, что, например,
![]() .
.
Если
же и
![]() ,
то в системе
,
то в системе![]() есть лишь два независимых уравнения, а
третье является их следствием. В силу
этого система сводится к двум уравнениям
с тремя неизвестными. Такая система
неопределенна и имеет бесчисленное
множество решений: одному можно придавать
любое значение, а остальные неизвестные
определяются из двух независимых –
все решения лежат на прямой, т.е. на
пересечении двух плоскостей. В этом
случае
есть лишь два независимых уравнения, а
третье является их следствием. В силу
этого система сводится к двум уравнениям
с тремя неизвестными. Такая система
неопределенна и имеет бесчисленное
множество решений: одному можно придавать
любое значение, а остальные неизвестные
определяются из двух независимых –
все решения лежат на прямой, т.е. на
пересечении двух плоскостей. В этом
случае![]() .
.
Если
же
![]() ,
то система несовместна и не имеет
решений. В этом случае среди определителей
,
то система несовместна и не имеет
решений. В этом случае среди определителей![]() ,
,![]() ,
,![]() есть хотя бы один, не равный нулю.
есть хотя бы один, не равный нулю.
Случай,
когда
![]() ,
т.е. равны нулю и все его миноры второго
порядка, но есть элементы, не равные
нулю, приводит к выражениям
,
т.е. равны нулю и все его миноры второго
порядка, но есть элементы, не равные
нулю, приводит к выражениям
![]() и
и
![]() .
.
Если
же и
![]() ,
,![]() ,
то в
,
то в![]() есть лишь одно независимое уравнение.
Система неопределенна, имеет бесчисленное
множество решений (точки плоскости). В
этом случае
есть лишь одно независимое уравнение.
Система неопределенна, имеет бесчисленное
множество решений (точки плоскости). В
этом случае![]() ,
и определители всех миноров второго
порядка также равны нулю.
,
и определители всех миноров второго
порядка также равны нулю.
Если
же
![]() ,
или
,
или![]() ,
то система противоречива и не имеет
решений – параллельные плоскости.
,
то система противоречива и не имеет
решений – параллельные плоскости.
Однородная система трех линейных уравнений с тремя неизвестными.
Однородной
называют систему, в которой
![]() ,
,![]() .
.
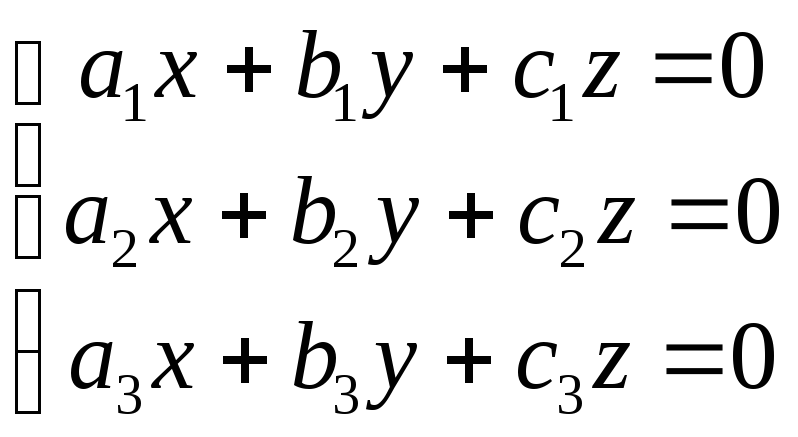 .
. ![]()
Система
![]() - неоднородна.
- неоднородна.
Если
![]() в
в![]() не равен нулю, то система имеет единственное
решение
не равен нулю, то система имеет единственное
решение![]() .
.
Если
же
![]() ,
то среди его строк есть линейная
зависимость и в
,
то среди его строк есть линейная
зависимость и в![]() остается два или одно независимое
уравнение.
остается два или одно независимое
уравнение.
Решение произвольных систем линейных уравнений
Пусть
задана система
![]() линейных
уравнений с
линейных
уравнений с![]() неизвестными,
неизвестными,![]() :
:
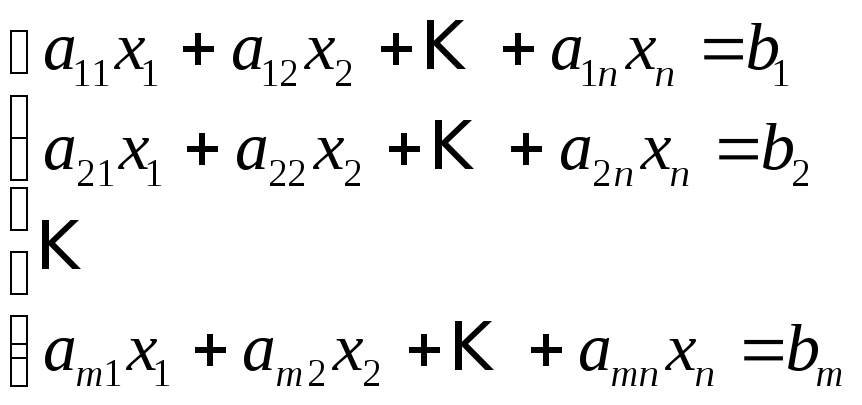 , (1)
, (1)
или в матричной форме
![]() , (2)
, (2)
где
![]() ,
,
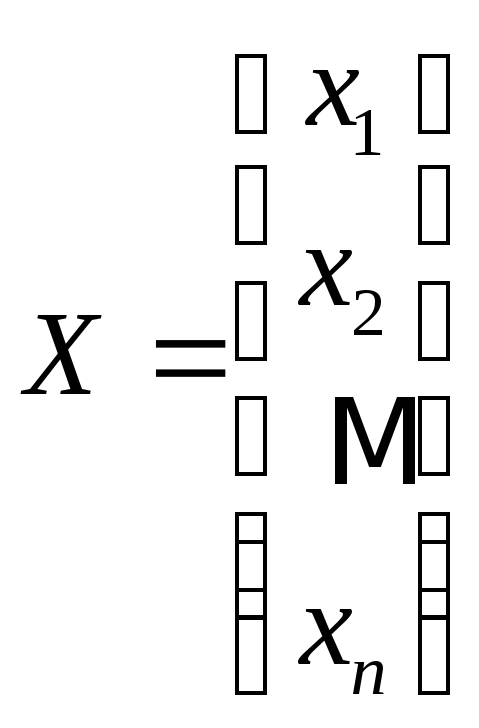 ,
,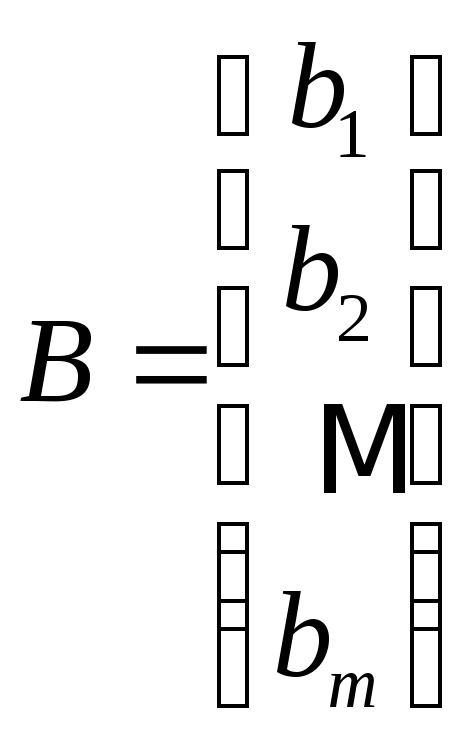 .
.
Решением
системы (1) или (2) называется любой
![]() -компонентный
вектор-столбец или матрица-столбец
-компонентный
вектор-столбец или матрица-столбец![]() ,
обращающий в верное равенство системы
(1) или (2).
,
обращающий в верное равенство системы
(1) или (2).
Система называется совместной, если у нее существует хотя бы одно решение. В противном случае, система несовместна. Две системы называют эквивалентными, если множества их решений совпадают.
Теорема Кронекера–Капелли. Чтобы система вида (1) была совместна, необходимо и достаточно, чтобы
![]() ,
,
где
![]() - расширенная матрица системы.
- расширенная матрица системы.
Пусть
теперь в системе (2)
![]() ,
т.е. она совместна. Можно считать, не
ограничивая общности, что не равный
нулю минор порядка
,
т.е. она совместна. Можно считать, не
ограничивая общности, что не равный
нулю минор порядка![]() располагается в первых
располагается в первых![]() строках и столбцах матрицы
строках и столбцах матрицы![]() .
.
Запишем
«укороченную» систему для (1), отбросив
последние
![]() уравнений, в виде:
уравнений, в виде:
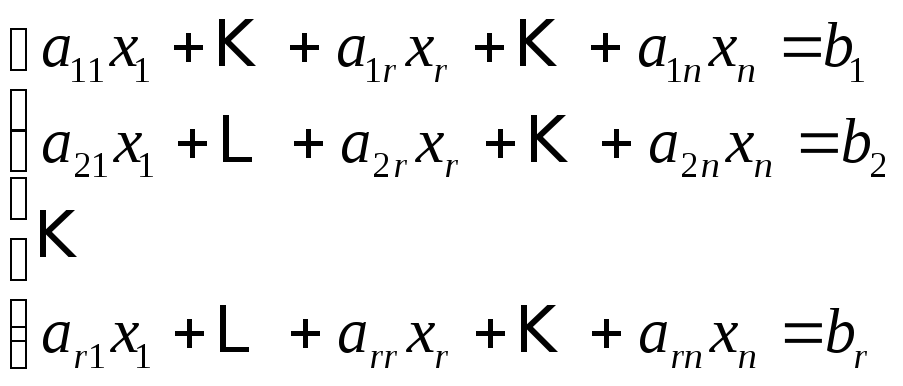 (3)
(3)
Эта система эквивалентна исходной, т.к. отброшенные уравнения являются линейной комбинацией оставшихся уравнений.
Неизвестные
![]() называют
базисными, а
называют
базисными, а![]() - свободными. Перенесем теперь свободные
переменные в правую часть (3). В результате
получим систему относительно базисных
неизвестных:
- свободными. Перенесем теперь свободные
переменные в правую часть (3). В результате
получим систему относительно базисных
неизвестных:
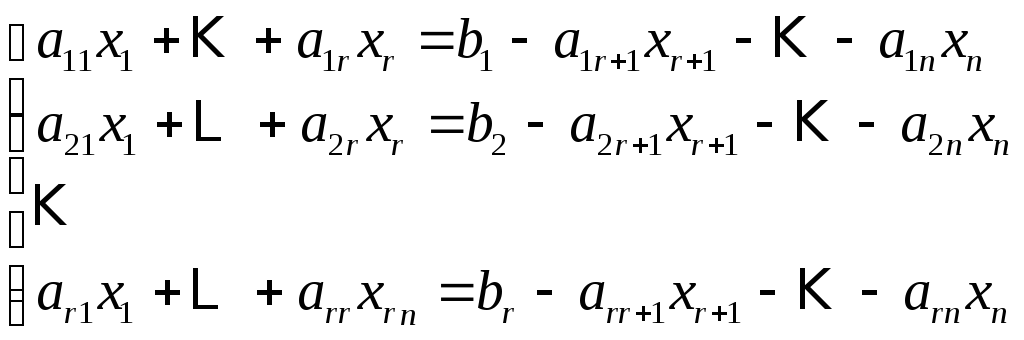 .
.
Эта система для любого набора значений свободных неизвестных имеет единственное решение:
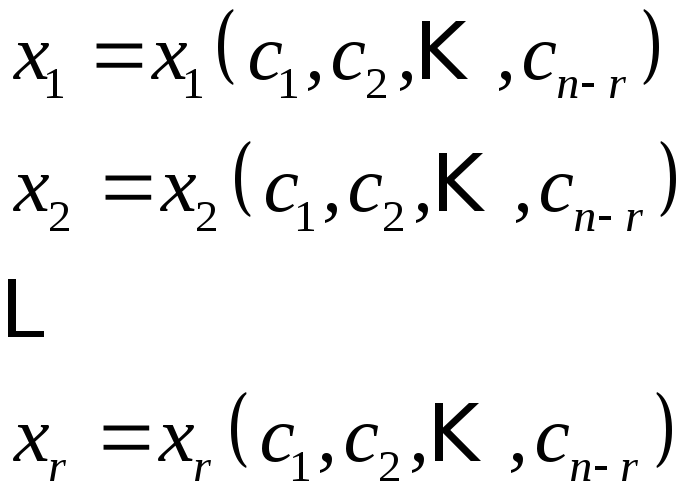 ,
,
где
![]() ,
,![]() ,
,![]() ,
,![]() — набор свободных неизвестных.
— набор свободных неизвестных.
Соответствующее решение укороченной, а следовательно и исходной системы имеет вид:
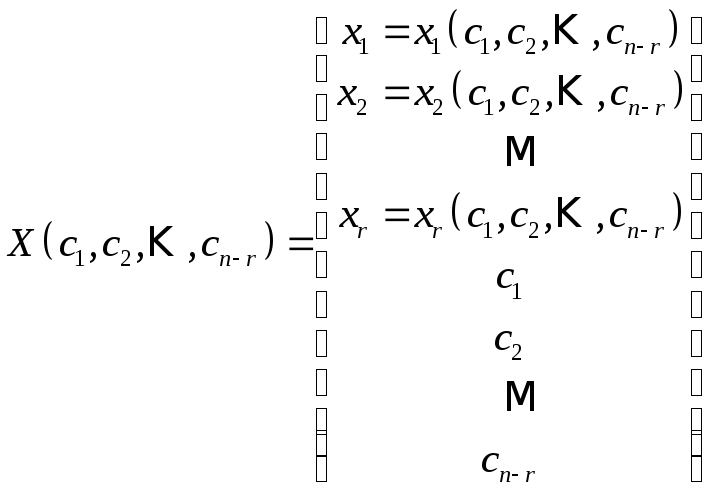 . (4)
. (4)
Формула
(4) выражает произвольное решение системы
(1) в виде функций от
![]() свободных неизвестных и называетсяобщим
решением
системы. Каждому конкретному набору
свободных неизвестных и называетсяобщим
решением
системы. Каждому конкретному набору
![]() соответствуетчастное
решение.
соответствуетчастное
решение.
