2.2.1.2. Многоканальная экспоненциальная смо

Многоканальная экспоненциальная СМО задается тремя параметрами: интенсивностью Λ прихода заявок, средним временем 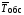обслуживания и числомК каналов (рис. 2.4).

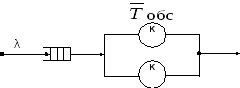
Рис. 2.4

Формулы для расчета характеристик многоканальной экспоненциальной СМО немногим сложнее (2.6)  (2.12).

Коэффициент загрузки определяется в виде

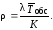
Его значение должно отвечать условно стационарности (2.8).

Средняя длина очереди в блоке ожидания

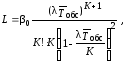
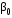
где  стационарная вероятность того, что в СМО нет заявок. Эта вероятность определяется в виде

=

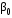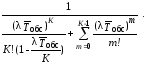
Остальные характеристики вычисляются через параметры СМО следующим образом:

М = L + K·ρ ; =;=+.

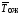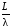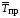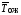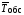Многоканальную СМО можно поставить в соответствие, например, многопроцессорному блоку вычислительной системы, имеющему общую память для всех процессоров и, следовательно, общую очередь задач.

2.2.1.3. Модель m/g /1

Для однолинейной системы массового обслуживания М/G/1 с пуассоновским потоком на входе, прямой процедурой обслуживания (первым пришел – первым обслужен) и произвольным распределением значений случайного времени обслуживания формула Полячека-Хинчина определяет среднее время ожидания начала обслуживания в виде

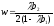, (2.13)

Здесь  – интенсивность входного простейшего потока заявок, 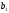– среднее время обслуживания,­­­­­­­­­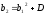 – второй момент распределения длительности обслуживания (D – дисперсия).

Заявка перемещается в очереди в среднем с постоянной скоростью. Среднее число переходов заявки в очереди на одно место вперед за единицу времени равно . При такой скорости переходов за время w заявка совершит L_c переходов. Это есть средняя длина очереди, т.е.

L_c = w (2.14)

Подставляя в (2.14) вместо w его определение (2.13), получаем выражение для средней очереди СМО М/G/1 в виде

L_c = 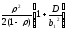(2.15)

Здесь 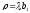– коэффициент загрузки СМО.

Из (2.15), в частности, следует, что для модели М/М/1 (экспоненциальное время обслуживания), когда D =, для средней длины очереди справедливо соотношение

L_cэ =

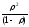
При фиксированном (постоянном) времени обслуживания D = 0, и

L_cп =

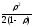
Для описания пульсирующего потока часто используется распределение Парето с плотностью распределения вероятностей вида

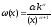;  > 0; х > 0,

где α – параметр формы, k – нижний граничный параметр, т.е. минимальное значение для случайной переменной х. При α > 1 имеет место конечное среднее (м.о.) M(x) = αK/(α – 1), при α > 2 – конечная дисперсия D(x) = M(x²)  – M²(x) = αK ²/(α – 1)²/(α – 2).

Подставляя эти значения в (2.15), получаем выражение для оценки среднего значения очереди при времени обслуживания, оаспределенным по Парето

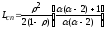(2.16)

Сопоставляя (2.16) с (2.15) определяем значение α = (1+). Это значение является пороговым, при превышении которого для экспоненциальной СМО М/М/1 средняя длина очереди оказывается большей, чем для СМО с пуассоновским входным потоком и распределенным по Парето временем обслуживания при одинаковой входящей нагрузке.