9. Планирование статистического эксперимента

Задача планирования. Пусть X =(x₁, ... , x_k)  вектор случайных величин, имеющий распределение Р_Х. Во многих случаях цель статистического эксперимента может быть сведена к определению математического ожидания с.в. y=g(X), где g(X)  заданная функция распределения с.в. X. Типовая схема статистического эксперимента имеет следующий вид (рис. 9.1).

Здесь оценка 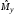приближается к точному значениюM(y) с ростом числа опытов n. Задача планирования статистического эксперимента состоит в нахождении такого n, при котором достигается заданная точность оценки .

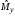i = 1...n

g(X)

y_i

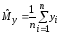
X_i

Рис. 9.1. Типовая схема статистического эксперимента:

X_i ~ P_Y; X_i = (x_1i ,..., x_ki);

y_i  значение с.в. Y в i-м опыте;

n  число опытов

Теоретическое решение задачи планирования. Оценка 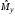является случайной величиной, так как представляет собой функцию от случайных величин:

(9.1)

В типовой схеме статистического эксперимента (рис. 3.17) используются независимые реализации x_i , поэтому с.в. y_i в формуле (9.1) также независимы. Из центральной предельной теоремы вытекает, что с.в. 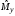в (9.1) при большихn имеет нормальное распределение, т.е. 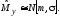Определим параметры этого распределения:

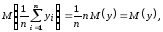(9.2)

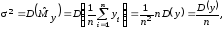
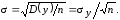(9.3)

Таким образом, при увеличении числа опытов на порядок  уменьшается в 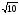3 раза. На рис. 9.2. схематически показан вид распределения оценки 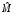в зависимости отn.

Рис. 9.2. Распределение с.в. 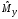в зависимости отn

Диапазон вероятных отклонений оценки от точного значения M(y) сужается пропорционально 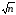. Параметр используют как показатель точности оценки. Поскольку 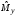имеет нормальное распределение, то практически достоверно, чтоотклоняется от искомогоM(y) не более чем на 3. Можно сказать, что  является аналогом абсолютной погрешности, а 3  самой абсолютной погрешностью. В качестве аналога относительной погрешности для с.в. 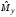можно рассматривать ее коэффициент вариации:

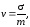
а в качестве самой относительной погрешности  величину 3v. Из (9.2) и (9.3) находим, что

(9.4)

где v_y  коэффициент вариации с.в. y.

Соотношения (9.3) и (9.4) показывают, что "абсолютная погрешность"  3 и "относительная погрешность"  3v оценки 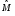убывают пропорционально.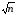

Из формулы (9.3) находим решение задачи планирования: для достижения заданной точности  требуется n опытов

(9.5)

Если требование к точности задано в форме коэффициента вариации v, то требуемое число опытов определяется из формулы (9.4) в виде:

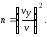(9.6)

В решении (9.5) кроме заданного  для определения n необходимо знать _у, в варианте (9.6)  коэффициент вариации v_у. Ни то, ни другое до эксперимента, как правило, не известно. Поэтому планирование числа опытов на практике осуществляется в ходе самого статистического эксперимента. Достаточно удобными методами такого планирования являются метод автоостанова.

Метод автоостанова. Схема статистического эксперимента с автоостановом изображена на рис. 9.3. Покажем на примере достижения точности v=0,01.

Как видно из рисунка, в ходе эксперимента ведется непрерывный контроль за оценкой v' коэффициента вариацииv. Когда оценкаv'устойчиво входит в зонуv'<0,01, эксперимент завершается.

Устойчивое достижение неравенства v'< 0,01 здесь обеспечивается требованием, чтобы это неравенство было подтверждено A=10 раз.

Заметим, что минимальное начальное значение счетчика подтверждений на рис. 9.3, задаваемое в начале алгоритма, должно составлять A=2, так как необходимо исключить одно ложное подтверждение, которое имеет место приn=1. Действительно, приn=1 оценка дисперсии равна нулю, поэтому получаетсяv'=0. ПриA=10 получится несколько "лишних" повторений цикла. Однако так какn обычно составляет десятки тысяч, то увеличение его на несколько лишних единиц не имеет существенного практического значения.

Рис. 9.3. Схема эксперимента с автоостановом

Как видно из ИСнка, в ходе эксперимента ведется непрерывный контроль за оценкой v' коэффициента вариации v. Когда оценка v' устойчиво входит в зону v' < 0.01, эксперимент завершается.

Устойчивое достижение неравенства v' < 0.01 здесь обеспечивается требованием, чтобы это неравенство было подтверждено A = 10 раз.

Заметим, что минимальное начальное значение счетчика подтверждений на рис. 9.3., задаваемое в начале алгоритма, должно составлять A = 2, т.к. необходимо исключить одно ложное подтверждение, которое имеет место при n = =1. Действительно, при n = 1 оценка дисперсии равна нулю, поэтому получается v' = 0. При A = 10 получится несколько "лишних" повторений цикла. Однако, так как n обычно составляет десятки тысяч, то увеличение его на несколько лишних единиц не имеет существенного практического значения.