8. Тестирование имитационной модели

Когда составлена программа моделирования, её проверяют с помощью тестов, т.е. решая задачи с заранее известными ответами.

Пошаговое тестирование состоит в проверке правильности выполнения алгоритма по шагам. В простых случаях можно рассчитать значения переменных для нескольких первых шагов и убедиться, что ЭВМ выдаёт те же значения. В более сложных случаях можно ограничиться выводом значений переменных для первых шагов и анализом этих данных с позиций здравого смысла. Например, если оказалось, что приборы принимают заявки на обслуживание, но ни на одном шаге не происходит освобождение прибора, значит, явно где-то ошибка. Для наглядности можно строить временные диаграммы, демонстрирующие изменения состояний приборов во времени, изменение числа заявок в системе и т.п.

Наряду с пошаговым тестированием необходимо проводить статистическое тестирование хотя бы потому, что никаким пошаговым тестированием не проверить программу генерирования случайных чисел. Если датчик случайных чисел не обеспечивает нужного закона распределения, то оценка оказывается смещённой даже при правильном её построении и правильном алгоритме имитации. Статистическое тестирование проводится путём сравнения полученного значения оценки о точным значением оцениваемой характеристики, найденным теоретическим путём. Так как оценка имеет случайный характер, точного совпадения не будет. Насколько сильно должна отклониться оценка от точного значения, чтобы разница была признана недопустимой и потребовалось выяснение причины такого отклонения? Ответ зависит от назначенного коэффициента доверия. Наиболее распространённым в практике значением коэффициента доверия является 0.95. При этом пороговым значением при принятии решения является величина 2. При таком пороге в пяти процентах случаев (более точно – 4.5%) отклонение, превысившее порог, будет вполне естественным, а отрицательный результат теста будет фактически «ложной тревогой». Но в подавляющем большинстве случаев (95.5%) отклонение, превышающие 2, всё же говорит о каком-то неблагополучии. Обнаружив такое отклонение, надо, прежде всего, получить ещё одну выборку и убедиться, что тревожный предыдущий результат не был ложной тревогой. Если снова отклонение окажется недопустимо большим, значит либо тестовые данные (точное значение) ошибочны, либо программа моделирования выдаёт неправильные оценки. Надо выяснить причину. Подготовка тестовых данных при моделировании СМО требует значения теории массового обслуживания. Приведём без доказательства простой способ расчёта тестовых данных, который пока отсутствует в учебниках и книгах по теории массового обслуживания. Изложить его проще всего на конкретном примере.

Пример.Рассматривается СМО с тремя приборами и двумя ячейками буфера. Имеется пять источников заявок одного типа. Интервал между заявками отельного источника распределён по экспоненциальному закону со средним значением Т. Время обслуживания заявки распределено тоже по экспоненциальному закону, но со средним значением Т₀.

На рис. 8.1 изображён граф, отражающий возможные состояния СМО и переходы из одного состояния в другое. Цифра в кружочке указывает текущее количество заявок в системе. Это и есть характеристика состояния СМО. Например, в состоянии 4 заняты все три прибора и одна ячейка буфера. В состоянии 2 заняты два прибора; поскольку один прибор свободен, буфер, естественно, пуст.

На дугах указаны интенсивности переходов, где =1/T- интенсивность потока заявок одного источника, =1/T₀- интенсивность обслуживания. Предполагается, что источники заявок имеют конечную ёмкость, равную

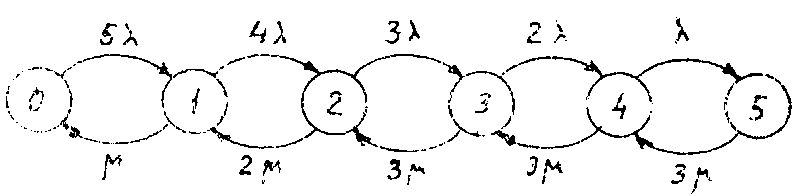
Рис.8.1. Граф состояния СМО.

единице. Это означает, что источник, выдав заявку, оказывается пустым и ждёт, пока его заявка вернётся в этот источник по окончании обслуживания. После возврата заявки в источник она вновь выдаётся через случайный интервал времени, распределение которого указано выше. При единичной ёмкости источника под интервалом между заявками следует понимать время от возврата заявки в источник до выдачи заявки. Это как бы время, требующееся для подготовки очередной заявки. При бесконечной ёмкости источника время подготовки заявки совпадает с интервалом между заявками.

В состоянии 0 в каждом из пяти источников находится по одной заявке, любой из них может выдать заявку, поэтому интенсивность перехода 0®I равна 5. По мере увеличения числа заявок в системе обслуживания уменьшается число источников, содержащих заявку, поэтому интенсивности переходов, связанных с выдачей заявки, уменьшается от 5 до . В случае, когда источники обладают бесконечной ёмкостью, на всех дугах, идущих слева направо, будут интенсивности 5.

Дуги нижнего ряда связаны с переходами, обусловленными окончанием обслуживания заявок. Например, в состоянии 4, когда заняты три прибора (четвёртая заявка находится в буфере), любой из трёх приборов может завершить обслуживание заявки, поэтому интенсивность перехода 4®3 равна 3. В состоянии 2 заняты только два прибора, поэтому интенсивность перехода 2®1 равна 2.

Вычисление вероятностей состояний применительно к установившемуся режиму работы легко осуществляется по графу состояний. Для каждой вершины вычисляются величины, которые назовём индексами и обозначим А. Чтобы вычислить А_i–индексi-й вершины, надо выделить подграф, состоящий из путей, ведущих к этой вершине. Подграф должен содержать по одной дуге, выходящей из каждой вершины, кроме корневой, т.е. i-й. Примеры подграфов приведены на рис.8.2. Для наглядности обозначены только корневые вершины.

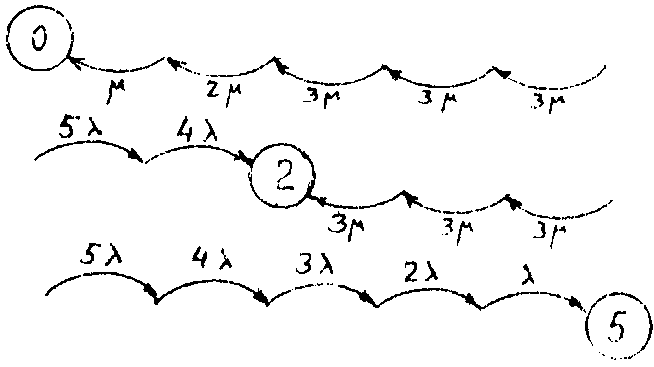
Рис.8.2. Подграфы для вычисления индексов вершин.

Индекс вершины вычисляется как произведение интенсивностей, указанных на дугах подграфа. Индексы вершин для данного примера следующие:

А₀=*2*(3)³, А₃=5*4*3*(3)², А₁=5*2*(3)³,

А₄=5*4*3*2*3, А₂=5*4*(3)³, А₅=5*4*3*2*,

При небольшом навыке можно сразу написать формулы для индексов, глядя на исходный граф и мысленно выделяя пути, ведущие к корневой вершине. Следует предупредить, что для графов более сложной структуры (имеющих ответвления, перескоки дуг через соседние вершины и т.д.) методика вычисления индексов вершин иная и требует отдельного описания.

Вероятность того, что в произвольный момент времени в системе находится i заявок, вычисляется по формуле:

По вероятностям Р_iможно вычислить целый ряд характеристик СМО. Приведём примеры. Вероятность того, что все приборы заняты, равна Р₃+Р₄+Р₅. Вероятность того, что буфер пуст, равна Р₀+Р₁+Р₂+Р₃. Коэффициент загрузки прибора равен К_зп = (Р₁+Р₂*2+(Р₃+Р₄+Р₅)*3)/3.

Коэффициент загрузки буфера К_зп = Р₄+Р₅*2)/2. Вероятность потери заявки равна Р₅, так как при экспоненциальных законах распределения она совпадает с вероятностью полной занятости. При других законах распределения это не так. Следует помнить, что описанная методика расчета вероятностей состояний верна только при экспоненциальных законах распределения интервалов между заявками и длительностей обслуживания.

Рассмотрим пример статистического тестирования. Допустим, были получены выборочные значения оценки вероятности потери заявки в результате моделирования двухканальной СМО с отказами при экспоненциальных законах распределения: 0.204, 0.197, 0.192, 0.226, 0.192, 0.177, 0.206, 0.191, 0.199, 0.182. Воспользуемся описанной методикой, чтобы подсчитать точное значение вероятности потери заявки Р_потдля этого случая.

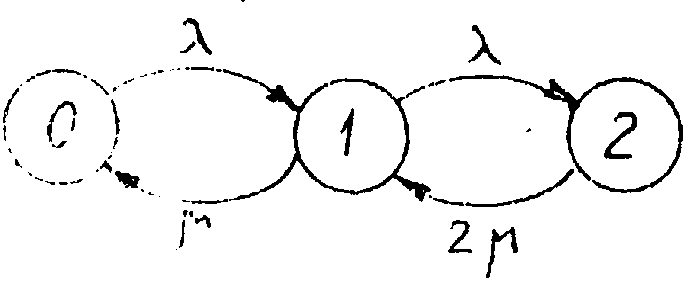
Рис. 8.3. Граф состояний двухканальной СМО.

По графу состояний (рис.7.3) нетрудно написать индексы вершин

А₀=2², А₁=2, А₂=².

Отсюда находим вероятность полной занятости Р₂, которая совпадает с вероятностью потери заявки Р_пот, так как в этом примере законы экспоненциальные

Р_пот=Р₂=А₂/(A₀+A₁+A₂₎=²/(2²+2+²⁾.

Математические ожидания Т и Т₀задавались равными единице, поэтому обратные им значения интенсивностей  и  тоже равны единице. Подставляя ==1 в формулу, находим Р_п=0.2.

В качестве оценки 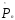примем среднее арифметическое приведённых выше десяти оценок,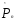=0.197. Оценка среднеквадратического отклонения=0.014. Учитывая, что среднее из десяти значений имеет среднеквадратическое отклонение в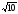раз меньше, чем каждое из значений, получаем  = ₁/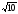»0.004. Видим, что отличие оценки от точного значения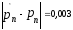, не превысило , а допускается 2. Следовательно, тест прошёл успешно.

Один успешно закончившийся тест ещё не свидетельствует о правильности программы моделирования. Как хорошо известно, исчерпывающее тестирование вообще невозможно, так что абсолютно уверенно утверждать, что программа правильна, нельзя никогда. Однако степень уверенности в правильности программы возрастает с каждым успешно проведённым тестом. В то же время достаточно одного неудачно завершившегося теста, чтобы перестать доверять выдаваемым программой результатам и приступить к выяснению причины несоответствия. Нередко отрицательный результат тестирования объясняется простой невнимательностью: в программу введены исходные данные, не соответствующие тем, при которых вычислялось точное значение.

Одной из возможных причин неудачного тестирования может быть отличие характеристик последовательности случайных чисел от требуемых. Экспоненциально распределённые случайные числа получаются из базовых случайных чисел. Базовые случайные числа должны быть равномерно распределены в интервале [0,1] и некоррелированы.

Вопросы и задания:

1. Почему пошаговое тестирование необходимо дополнить статистическим тестированием?

2. Почему при статистическом тестировании необходимо осуществлять не один прогон программы, а несколько, хотя бы десяток?

3. Во сколько раз разница между оценкой и точным значением может превышать среднеквадратическое отклонение оценки, чтобы эта разница ещё считалась допустимой?