8.3.1.Векторный потенциал цилиндрического вибратора:

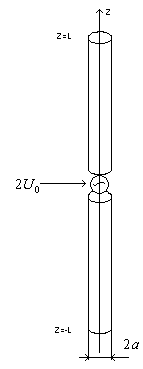
Рис. 8.3.1.

При выводе выражения для векторного потенциала будем исходить из содержания теоремы запаздывающих потенциалов и ряда приближений:

1. Антенна идеально проводящая: .

2. Радиус проводника антенны много меньше ее длины .

Вычислим векторный потенциал на поверхности антенны. Исходя из теоремы запаздывающих потенциалов в цилиндрической системе координат векторный потенциал определяется как:

Здесь: - координаты точки интегрирования,- координаты точки наблюдения,– расстояние между точкой наблюдения и точкой интегрирования,V– объем занимаемый токами. Учитывая наличие сильного скин-эффекта, будем считать, что ток течет в бесконечно тонком слое по поверхности проводника (рис.8.3.2.а).

а)идеальный проводник б) реальный металл

Рис. 8.3.2.

Таким образом, математически вектор плотности тока можно записать в виде: , здесь- неизвестная скалярная функция. Для ее определения подставим последнее выражение в известное соотношение:.

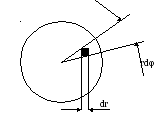
Рис. 8.3.3.

Элемент поверхности запишется так: , интеграл легко берется с учетом фильтрующего действия дельта- функции:

Отсюда окончательно получим: выражение для вектора плотности тока: .

Теперь можно окончательно записать векторный потенциал:

.

Для выражения расстояния между точками наблюдения и интегрирования выделим две точки на поверхности антенны и.

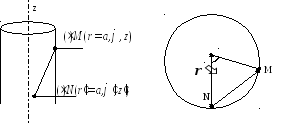
Рис. 8.3.4.

При можно воспользоваться теоремой косинусов:. Тогда для произвольныхмы можем записать:. Учитывая, что радиус антенны весьма мал, можно использовать приближенное среднее значение, не зависящее от угла. Действительно, из рис. 8.3.4. видно, что, в итоге получаем:

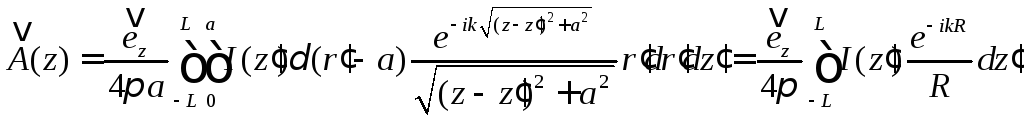. (8.3.1)

1. 8.3.2.Электрическое поле на поверхности цилиндрической антенны.

Как известно, связь электрического поля и векторного потенциала имеет вид:

. Найдемучитывая, что векторный потенциал имеет только одну продольную составляющую, как это видно из выражения (8.3.1) ::

,

Градиент этого выражения в силу зависимости только от координатыбудет иметь только-ую проекцию:

.

Теперь найдем электрическое поле:

. (8.3.2.)

Итак, мы получили выражение для вектора напряженности электрического поля, обусловленного током, протекающим по проводнику и зависящему от геометрии антенны, длины волны, свойств среды.

0. 8.3.3. Реализация граничного условия на поверхности антенны.

Электрическое поле на поверхности антенны обусловлено не только током, протекающим по проводнику антенны, но и внешним полем источника, называемым сторонним полем. В случае передающей антенны, возбуждаемой, как показано на рис.8.3.1. дельта-образным генератором напряжения стороннее поле может быть аппроксимировано выражением: . Граничное условие в таком случае запишется так:

Перенося второе слагаемое в правую часть, получим уравнение Поклингтона:

, (8.3.3.)

где:

,

8.4. Решение уравнения Поклингтона методом Галеркина.

Аналитического решения уравнения (8.3.3.) не найдено. Численное решение предполагает такие этапы:

1 Этап. Выбираем систему базисных функций, по которой раскладывается предполагаемое решение:

(8.4.1.)

Коэффициенты разложения называются базисными коэффициентами. В качестве базисной системы можно выбрать разнообразные функции, например:

(8.4.2.)

- эта функция удовлетворяет граничным условиям на концах антенны (т.е. при , рис. 8.3.5). Функции, отличные от нуля на всем интервале существования тока называются базисными функциями полной области. Помимо них, можно использовать базисные функции, отличные от нуля только на некотором интервале, меньшем , чем. В этом случае говорят о базисных функциях подобластей. Распространенным базисом подобластей для решения задач вибраторных излучателей является кусочно-синусоидальный базис.

Рис. 8.3.5.

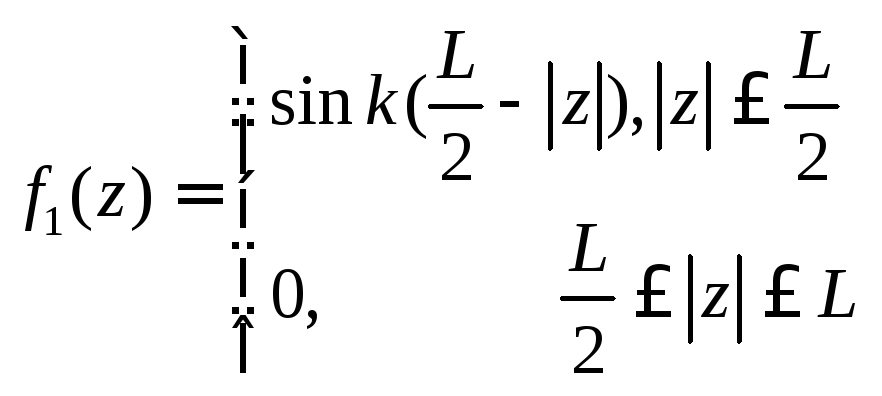, (8.4.3.)

,. ()

Графики этих функций и распределение тока представлены на рис.8.3.6. Из рисунков видно, что в этом случае граничные условия на концах также выполняются автоматически.

Рис. 8.3.6.

Конкретный вид базисных функций выбирается с учетом физического содержания задачи, выполнения требований граничных условий и быстрой сходимости решения. Типы базисных функций для решения задач электродинамики далеко не ограничивается видом (8.4.2.) или (8.4.3.).Выбор вида базисных функций имеет большое значение, так как от этого зависит число членов Nв разложении (8.4.1) и, следовательно, порядок СЛАУ. В конечном счете, от этого зависит время решения на ЭВМ. Примерами базисных функций полной области являются синусоидальные функции, функции Чебышева, степенные функции и т.д. Среди базисных функций подобластей следует выделить кусочно-постоянные (импульсные), кусочно-линейные, кусочно-синусоидальные и другие. Подробнее с представлениями решений в виде разложений по перечисленным базисам можно познакомиться в [4].

2 Этап. Подставляя разложение (8.4.1) в исходное интегральное уравнение (8.3.3) и меняя порядок суммирования и интегрирования, получаем:

(8.4.4)

Таким образом, интегральное уравнение (8.3.3.), сформулированное относительно функции распределения тока заменяется на уравнение (8.4.4), относительно неизвестных комплексных коэффициентов (базисных коэффициентов). Уравнение (8.4.4) в таком виде неразрешимо, необходимо иметьусловий. Для получения этих условий реализуется процедура Галеркина.

3 Этап. На этом этапе выполняется алгебраизация, т.е. сведение исходного уравнения к системе линейных алгебраических уравнений (СЛАУ). Для этого выбирается система так называемых весовых (проекционных) функций,. В частном случае она может совпадать с системой базисных функций. Такая разновидность метода моментов носит название метода Галеркина. Затем, для формирования СЛАУ обе части уравнения (8.4.4) последовательно умножаются надля всех, и интегрируются по длине антенны. В результате получаем алгебраическую систему:

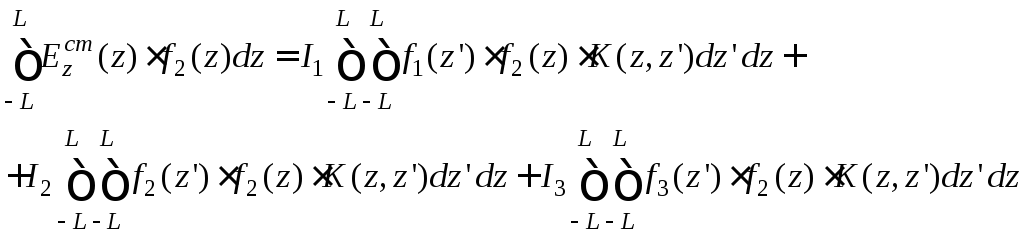
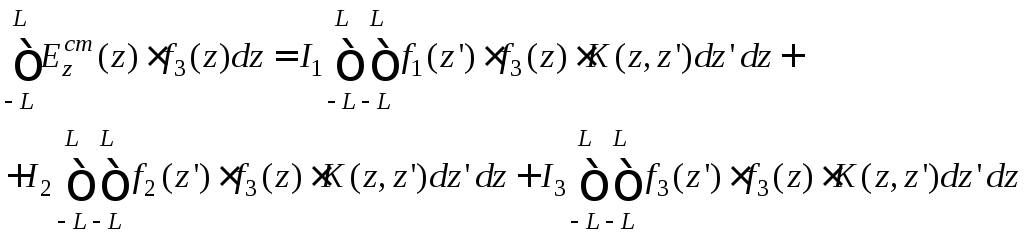
Приведенную систему уравнений можно записать в более лаконичном виде:

,

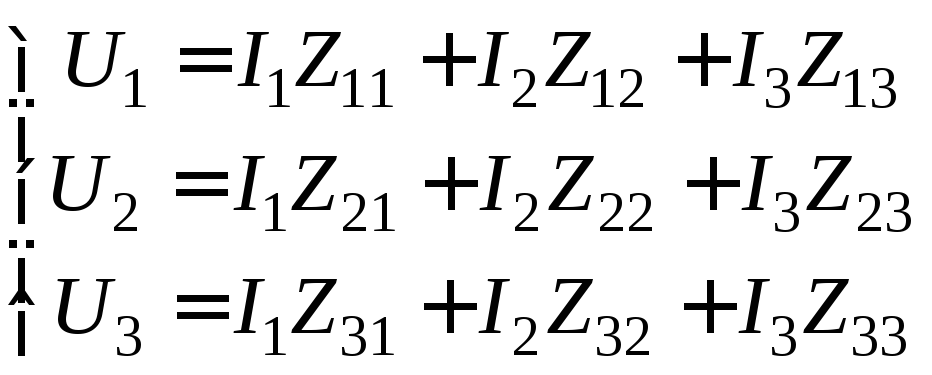где 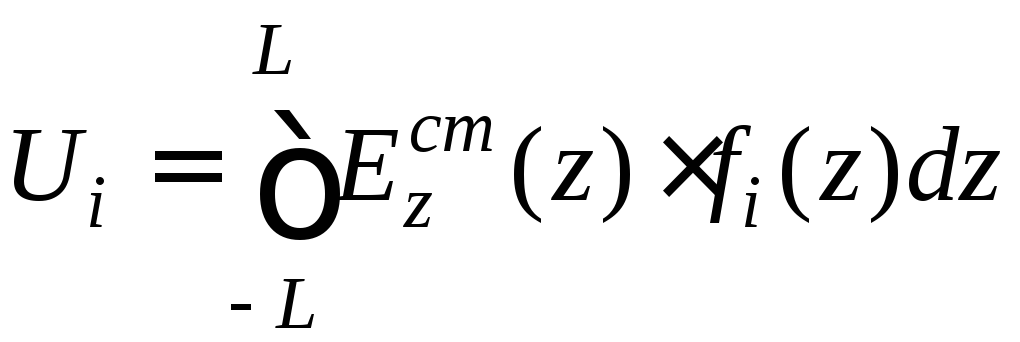, (8.4.5)

, (8.4.6)

В матричной форме полученное СЛАУ примет следующий вид:

. (8.4.7)

В качестве функций могут быть выбраны, например, дельта-функции вида:. Практически это означает, что интегральное уравнение должно удовлетворяться только в отдельных точках интервала (длины антенны). Этот случай называется методом сшивания в точках или методом коллокации. При большом числе точек сшивания, равномерно распределенных по всей области интегрирования, реше­ние приближается к точному. Преимущество метода коллокации зак­лючатся в простоте вычислений внутреннего интеграла в выраже­нии (8.4.6). Далее следует решать систему (8.4.5) относительно неизвестных базисных коэффициентови, затем, подставив их в выражение (8.4.1), можно восстановить искомое распределение тока в явном виде. Физический смысл деления вибратора на отрезки при задании на каждом отрезке формы распределения тока, соответствующей форме базисной функции, и последующей алгебраизации интегрального уравнения сводится к замене исходной антенны системой перекрывающихся коротких парциальных элементов (сегментов), которые взаимодействуют друг с другом. В результате взаимодействия в системе установились определенные амплитуды токов в каждом сегменте (соответствующие найденным базисным коэффициентам). Таким образом, фактически установлено соответствие между исходной непрерывной антенной системой и ее дискретными составными частями.

Рис.8.3.7. Геометрия исходной и ее аппроксимация сегментами.

Вычисление интегралов в левой части системы (8.4.7) уравнений не составляет труда: подставляя в выражение стороннее воздействие и соответствующую базисную функцию и воспользовавшись фильтрующим свойством дельта функции можно записать:

, (8.4.8)

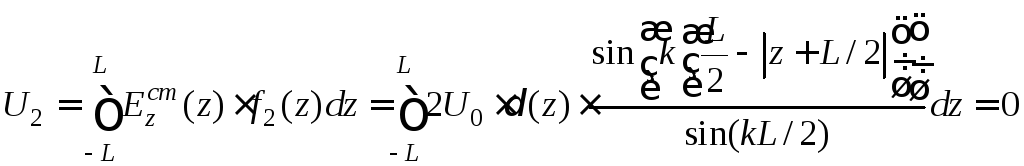, (8.4.9)

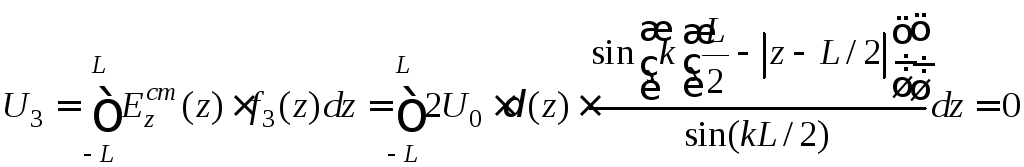, (8.4.10)

Вычисление взаимных импедансов в (8.4.7) представляет собой наиболее трудоемкую процедуру, на которую уходит основная часть машинного времени при численном решении интегрального уравнения. Удается путем двукратного применения процедуры интегрирования по частям свести двойные интегралы в СЛАУ (8.4.7) к однократному. Не повторяя подробно этот вывод, который можно найти в [Марков], приведем окончательный результат:

, (8.4.11)

где ,

,,

Теперь перейдем к упрощению матрицы правых частей СЛАУ с учетом симметрии исходной задачи.

Очевидно, что для симметричной вибраторной антенны в силу очевидного соотношения базисный коэффициент, определяющий ток, протекающий по левому сегменту, равен коэффициенту правого .

Кроме того, в силу одинакового разбиения правого и левого плеча вибраторной антенны можно утверждать, что электромагнитное взаимодействие ряда сегментов одинаковое, в частности:

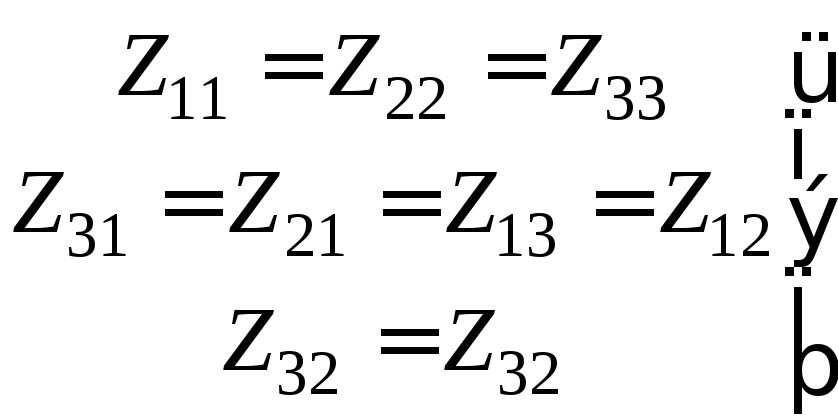, (8.4.12)

Учитывая эти особенности систему уравнений можно существенно упростить, оставив лишь два уравнения с двумя неизвестными:

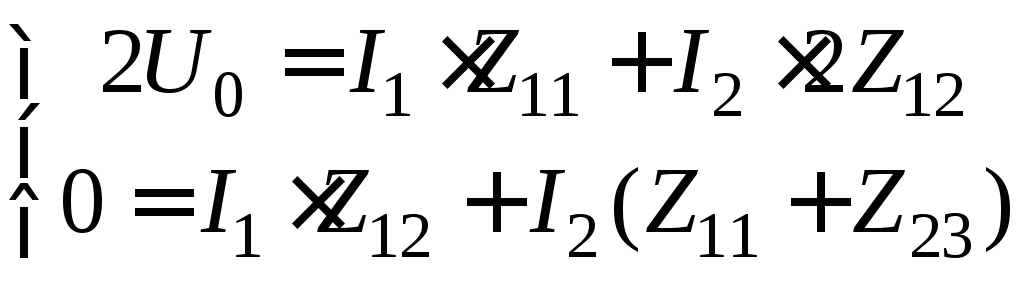, (8.4.13)

4 Этап.Выполняется решение СЛАУ.

Из приведенной системы уравнений можно определить базисные коэффициенты в явном виде через коэффициенты СЛАУ :

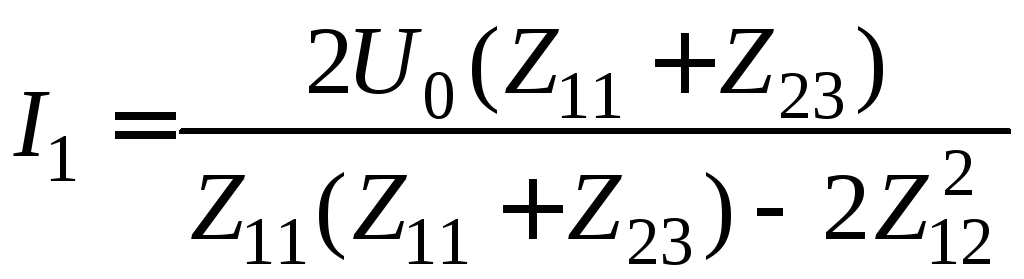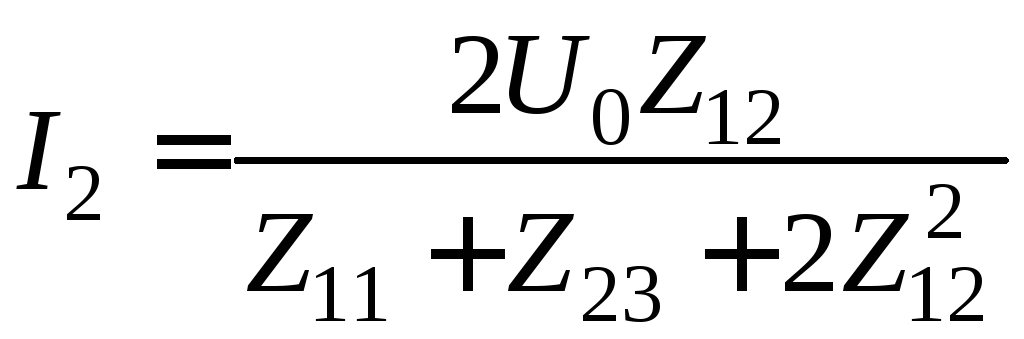, (8.4.14)

5 Этап.Восстановление искомой функции распределения тока и нахождение по нему основных характеристик антенны.

По найденному токовому распределению, на основе ранее найденного соотношения (4.2.) легко найти диаграмму направленности, которая будет комбинацией трех функций с теми же коэффициентами.

Выражение для входного импеданса антенны можно записать в явном виде:

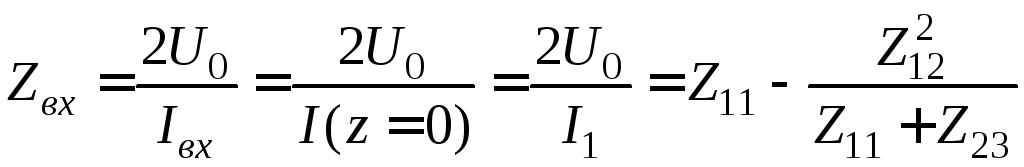(8.4.15)