§10. Сложение гармонических колебаний одного направления и одинаковой частоты

Колеблющееся тело может участвовать в нескольких процессах. Найдем результирующее колебание, т.е. сложим гармонические колебания одного направления и одинаковой частоты. Пусть складывается два колебания. Представим каждое гармоническое колебание методом вращающегося вектора амплитуды.

Пусть:

.

(10.1)

Графически изобразим эти колебания. Т.к. вектораА₁ иА₂ вращаются с одинаковой угловой скоростью _о, то разность фаз между ними ( ₂ – ₁ ) остается постоянной, и уравнение результирующего колебания будет иметь вид :

.

(10.1)

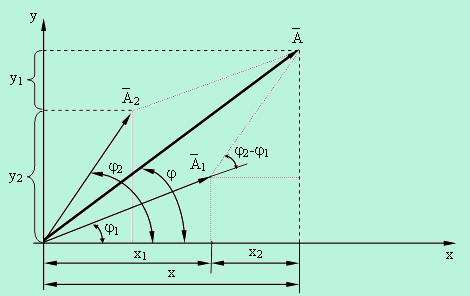
Рис.10.1. Сложение гармонических колебаний одного направления и одинаковой частоты



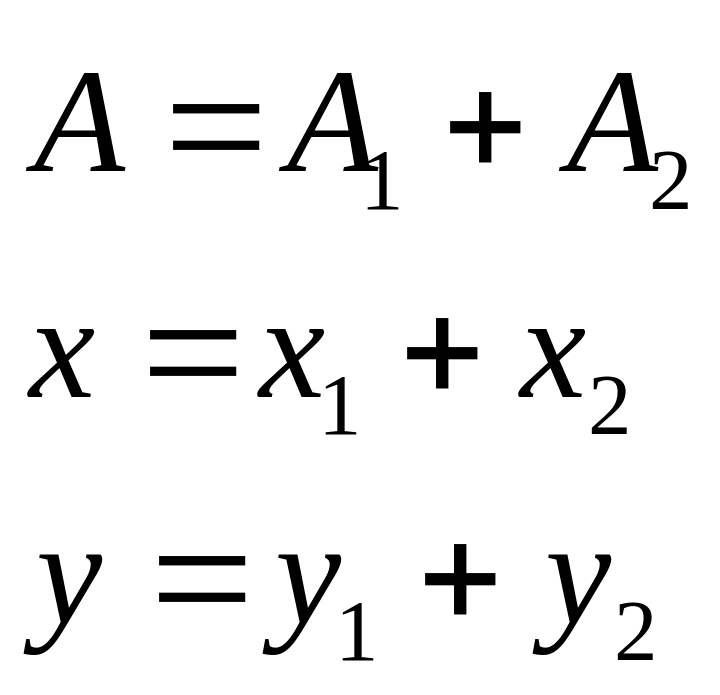
Из рисунка:

По теореме косинусов А² = А²₁ + А²₂ + 2А₁А₂ cos (₂ - ₁)/

	.	(10.2)
	.	(10.3)

Т.е., тело, участвуя в двух гармонических колебаниях одного направления и одной частоты, совершает также гармонические колебания в том же направлении и с той же частотой, что и складываемые колебания. Амплитуда результирующего колебания зависит от разности фаз складываемых колебаний.

Как же будет изменяться величина амплитуды в зависимости от разности фаз (₂ - ₁)

1) ₂ – ₁ =  2m ( m = 0,1,2,3,.....), то

А = А₁ + А₂ – амплитуда результирующего колебания равна сумме амплитуд складываемых колебаний.

2) ₂ – ₁ =  ( 2m + 1 ) ( m = 0,1,2,3,.....)

А = | А₁ – А₂ | – амплитуда результирующего колебания равна разности амплитуд складываемых колебаний.

Биения

Если два складываемых гармонических колебаний одинакового направления мало отличаются по частоте, то возникают биения.

Биениями называют периодические изменения амплитуды колебания, возникающие при сложении двух гармонических колебаний с близкими частотами.

Пусть

х₁ = A₁ cos t

х₂ = A₂ cos ( + ) t , тогда х = А cos t

Амплитуду А найдем по теореме косинусов:

если А₁=А₂ ₀₁ = ₀₂ = 0 тогда

cos (x+y) = cos x·cos y – sin x·sin y

1 + cos2x = 2cos²x

	.	(10.4)
		(10.5)

уравнение биений

Т. к.  / 2 <<  , то (10.5) почти не изменяется за то время, когда cos  t совершит полное колебание частоты изменения амплитуды биения в два раза больше частоты изменения косинуса ( т. к. берется по модулю ).

,

(10.6)

тогда частота биений равна разности частот складываемых колебаний.

.

(10.7)

График результирующего колебания дают жирные линии, а огибающие их – график изменения с течением времени амплитуды.

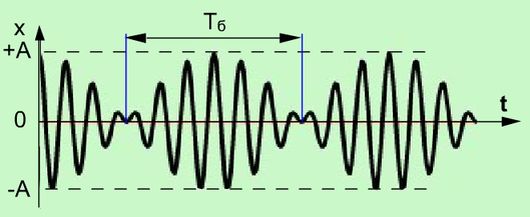
Рис. 10.2. Биения

Метод биений используется для настройки музыкальных инструментов, анализа слуха.

Любые сложные периодические колебания S = f (t) можно представить в виде суперпозиции одновременно совершающихся гармонических колебаний с различными амплитудами, начальными фазами, а также частотами кратными циклической частоте _о:

(10.8)

Представление периодической функции в виде (10.8) связывают с понятием гармонического анализа сложного периодического колебания или разложения Фурье (Фурье – французский математик).

Слагаемые ряда Фурье, определяющие гармонические колебания с частотами _о , 2_о , 3_о, ... называются первой (основной), второй, третьей, и т.д. гармониками сложного периодического колебания.