3. Колебания физического маятника

Физическим маятником называется твердое тело, совершающее колебания под действием силы тяжести вокруг неподвижной горизонтальной оси, не проходящей через центр масс С тела.

OC = l,

OO= L

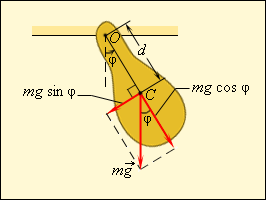
Рис.4.2. Колебания физического маятника

Если маятник отклонен из положения равновесия на угол , то уравнение динамики вращательного движения твердого тела можно записать так:

М = J;

 = ;

M = F_r l

Вектор возвращающей силы F_r противонаправлен с положительным направлением оси x.

,

(4.8)

т.к. угол  мал, то   sin .

Или

– mgl  = J  ,

тогда

(4.9)

или

,

(4.10)

тогда

		(4.11)
		(4.12)

приведенная длина маятника, т.е. L – длина такого математического маятника, период колебаний которого равен периоду колебаний физического маятника.

Точка О, отстоящая от точки О на продолжении прямой ОС на расстоянии приведенной длины L, называется центром качаний физического маятника.

По теореме Штейнера I = I_c + ml² , тогда

,

(4.13)

т.е. ОО всегда больше ОС.

Точка качаний и точка подвеса обладают свойством взаимозаменяемости.

§5. Фазовый портрет маятника. Адиабатический инвариант

Рассмотрим опять колебания пружинного маятника. Энергия системы определяется, как мы уже видели, следующим выражением:

.

(5.1)

Введем вместо скорости импульс: р= mx´. Тогда равенство (5.1) можно переписать в таком виде:

.

(5.2)

Разделим это равенство на W:

,

(5.3)

или

.

(5.4)

В «пространстве» с координатными осями x и p это уравнение эллипса с полуосями и . Пространство с осями «координата - импульс» называется фазовым пространством системы.

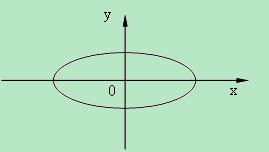
Рис 5.1. Траектория гармонического осциллятора в фазовом пространстве.

Таким образом, траектория гармонического осциллятора в фазовом пространстве представляет собой эллипс. А площадь эллипса, задаваемого уравнением: x²/a²+y²/b²=1. равна S = π a b, тогда площадь под фазовой траекторией определяется выражением:

,

(5.5)

или

.

(5.6)

Величина площади S, заключенной внутри фазовой траектории частицы, деленная на 2π, имеет в физике специальное название- адиабатический инвариант. Для гармонического осциллятора адиабатический инвариант определяется выражением:

.

(5.8)

Величина I была названа адиабатическим инвариантом потому, что мы рассматривали движение при неизменных параметрах системы, то есть приколебаниях пружинного маятника (грузика на пружинке) неизменным параметрами были масса грузика и коэффиицент жесткости пружинки, т.е. величина k, а значит и частота ω.

Равенство (5.8) справедливо не только для колебаний грузика на пружинке, но и для любой другой системы, совершающей гармонические колебания, параметры которой испытывают медленные вариации со временем. Например, это может быть математический маятник, длина которого медленно меняется со временем.
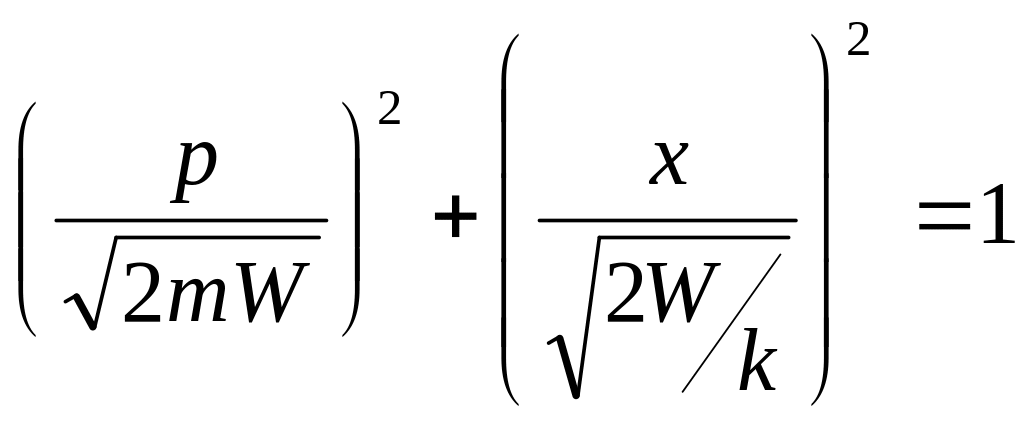